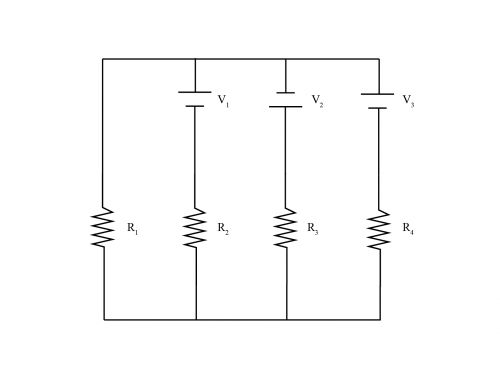
Para el circuito de la figura, encuentre:
(a) La capacitancia equivalente.
(b) La carga almacenada en el condensador 3.
(a) Para encontrar la capacitancia equivalente del circuito, necesitamos identificar grupos de capacitores que están en serie (que tienen la misma carga) o en paralelo (que tendrán el mismo voltaje), y aplicar las ecuaciones para la capacitancia equivalente en consecuencia. Necesitamos repetir este procedimiento hasta que reduzcamos el circuito a un solo capacitor (equivalente). Una vez que tenemos la capacitancia equivalente del circuito, podemos usar la definición de capacitancia y el diseño de los diferentes conjuntos de capacitores (es decir, si están conectados en serie o en paralelo) para encontrar sus cargas y voltajes. Podemos hacer esto secuencialmente a medida que expandimos el circuito desde un solo capacitor equivalente al circuito que se muestra en la primera figura.
[mepr-show rules=”4409″ unauth=”message”]
Como se muestra en la siguiente figura, los capacitores \ \( C_2 \) y \ \( C_3 \) comparten la misma conexión de cables continua en ambos extremos. Suponiendo que los cables tienen una resistencia insignificante, esto implica que \ \( C_2 \) y \ \( C_3 \) están sujetos al mismo voltaje y, por lo tanto, están conectados en paralelo. Para capacitores conectados en paralelo, la capacitancia equivalente es simple la suma de las capacitancias de cada capacitor. Por lo tanto, su capacitancia equivalente \ \( C’_1 \) está dada por
\begin{equation}
\label{EQ:CP1}
C’_1 = C_2 + C_3.
\end{equation}
Después de reemplazar \ \( C_2 \) y \ \( C_3 \) por su capacitor equivalente, el circuito se vuelve como se muestra en la siguiente figura.
Ahora, observe que \ \( C_1, C’_1 \) y \ \( C_4 \) están conectados contiguamente y el cableado entre ellos no se ramifica. Por tanto, están conectados en serie. Para un grupo de capacitores conectados en serie, la inversa de la capacitancia equivalente es igual a la suma de la inversa de las capacitancias de estos capacitores. Por lo tanto, la resistencia equivalente \ \( C’_2 \) de los capacitores \ \( C_1, C’_1 \) y \ \( C_4 \) está dada por
\begin{equation}
\ frac{1} {C’_2} = \ frac{1}{C_1} + \ frac{1} {C’_1} + \ frac{1}{C_4},
\end{equation}
e invertir las fracciones da
\begin{equation}
C’_2 = \ frac{1} {\ frac{1}{C_1} + \ frac{1} {C’_1} + \ frac{1}{C_4}}.
\end{equation}
Después de sustituir la ecuación \ eqref{EQ:CP1} en esta ecuación obtenemos
\begin{equation}
\label{EQ:CP2}
C’_2 = \ frac{1} {\ frac{1}{C_1} + \ frac{1} {C_2 + C_3} + \ frac{1}{C_4} }.
\end{equation}
Ahora, si reemplazamos \ \( C_1, C’_1 \) y \ \( C_4 \) con su capacitor equivalente, obtenemos el circuito que se muestra en la siguiente figura.
Hemos reducido el circuito a una sola resistencia conectada a la fuente. Por lo tanto, \ \( C’_2 \) es la capacitancia equivalente \ \( C _ {\ text{eq} } \) del circuito, es decir:
\begin{equation}
C _ {\ texto{eq} } = C’_2,
\end{equation}
y de la ecuación \ eqref{EQ:CP2} obtenemos:
\begin{equation}
C _ {\ texto{eq} } = \ frac{1} {\ frac{1}{C_1} + \ frac{1} {C_2 + C_3} + \ frac{1}{C_4} }.
\end{equation}
Finalmente, conectando valores numéricos nos da:
\begin{equation}
\label{EQ:CEQ}
C _ {\ texto{eq}} = \frac{1}{\ frac{1}{1 \ \ mu \ text{F}} + \frac{1}{2 \ \ mu \ text{F}+ 3 \ \ mu \ text{F}} + \frac{1}{4 \ \ mu \ text{F}}} = \ frac{20}{29} \ \ mu \ text{F} = 0,69 \ \ mu \ text{F} .
\end{equation}
(b) Ahora, necesitamos encontrar la carga almacenada en el Condensador 3. Recordemos que la capacitancia \ \( C \) de un capacitor se define como la carga \ \( Q \) almacenada en él dividida por la diferencia de potencial \ \( V \) a la que está sometido, es decir
\begin{equation}
\label{EQ:C}
C = \ frac{Q}{V}.
\end{equation}
Podemos reescribir esta expresión como:
\begin{equation}
\label{EQ:Q}
Q = CV,
\end{equation}
y
\begin{equation}
\label{EQ:V}
V = \frac{Q}{C},
\end{equation}
para encontrar la carga \ \( Q \) o el voltaje \ \( V \) en términos de las otras dos variables.
Ahora podemos usar las ecuaciones \ eqref{EQ:Q} y \ eqref{EQ:V} para encontrar las cargas y voltajes de todos los capacitores a medida que expandimos el circuito desde el que tiene una sola capacitancia equivalente en la cuarta figura hasta que obtengamos la carga del capacitor 3.
En el circuito reducido de la cuarta figura, la diferencia de potencial a la que \( C’_2 \) es la misma que el voltaje de la fuente. Esto se debe a que \ \( C’_2 \) está conectado a la fuente desde ambos extremos sin ningún otro componente en el medio. Por lo tanto, usando la ecuación. \ eqref{EQ:Q} podemos escribir la carga \ \( Q’_2 \) de este condensador como
\begin{equation}
\label{EQ:QP2}
Q’_2 = C’_2 V,
\end{equation}
donde \ \( C’_2 \) viene dado por la ecuación. EQ: CP2 y \ \( V = 12 \) V es el voltaje de la fuente. Dado que se conocen estas dos variables, se conoce el valor de \ \( Q’_2 \).
Recuerde que \ \( C’_2 \) es la capacitancia equivalente de los condensadores \ \( C_1, C’_1 \) y \ \( C_4 \), que están conectados en serie de acuerdo con la tercera figura. Por lo tanto, tienen la misma carga almacenada. En particular para \ \( C’_1 \) podemos escribir
\begin{equation}
Q’_1 = Q’_2,
\end{equation}
y sustituyendo la ecuación \eqref{EQ:QP2} obtenemos
\begin{equation}
\label{EQ:QP1}
Q’_1 = C’_2 V.
\end{equation}
Dado que ahora conocemos la carga y la capacitancia de este capacitor, podemos usar la ecuación. \ eqref{EQ:V} para encontrar su voltaje. El voltaje \ \( V’_1 \) del condensador \ \( C’_1 \) está dado por
\begin{equation}
V’_1 = \ frac {Q’_1} {C’_1},
\end{equation}
y sustituyendo la ecuación \eqref{EQ:QP1} se cumple que
\begin{equation}
\label{EQ:VP1}
V’_1 = \ frac {C’_2 V} {C’_1}.
\end{equation}
Ahora, \ \( C’_1 \) es la capacitancia equivalente de los capacitores \ \( C_2 \) y \ \( C_3 \), que están conectados en paralelo de acuerdo con la segunda figura. Por lo tanto, están sujetos al mismo voltaje. En particular, el voltaje \ \( V_3 \) del capacitor \ \( C_3 \) viene dado por
\begin{equation}
V_3 = V’_1,
\end{equation}
y sustituyendo la ecuación \eqref{EQ:VP1} obtenemos
\begin{equation}
\label{EQ:V3}
V_3 = \ frac {C’_2 V} {C’_1}.
\end{equation}
Finalmente, de la ecuación \ eqref{EQ:Q} , la carga del condensador 3 viene dada por
\begin{equation}
Q_3 = C_3 V_3,
\end{equation}
y sustituyendo la ecuación \eqref{EQ:V3} se cumple que
\begin{equation}
Q_3 = C_3 \ frac {C’_2 V} {C’_1} = C_3 V \ frac {C’_2} {C’_1},
\end{equation}
donde \ \( C’_2 \) viene dado por la ecuación. \ eqref{EQ:CP2} y \ \( C’_1 \) viene dado por la ecuación. \eqref{EQ:CP1}. Si insertamos estas ecuaciones obtenemos
\begin{equation}
Q_3 = C_3 V \ frac {\ frac{1} {\ frac{1}{C_1} + \ frac{1} {C_2 + C_3} + \ frac{1}{C_4} }} {C_2 + C_3}.
\end{equation}
Finalmente, la sustitución de valores numéricos da
\begin{equation}
Q_3 = (3 \ \ mu \ text{F}) (12 \ \ texto{V}) \ frac {\ frac{1}{\ frac{1}{1 \ \ mu \ text{F} } + \frac{1}{2 \ \ mu \ text{F} + 3 \ \ mu \ text{F} } + \frac{1}{4 \ \ mu \ text{F}}}} {2 \ \ mu \ text{F} + 3 \ \ mu \ text{F} }
= \frac{144}{29} \ \ mu \ text{C} = 4.966 \ \ mu \ text{C} .
\end{equation}
[/mepr-show]




Leave A Comment