¡2 cargas en un eje!

a) Utilice la ecuación para el potencial eléctrico y conecte cada carga y su distancia correspondiente al punto A.

b) La misma sugerencia que se da en el inciso b).

c) Utilice la conservación de energía para obtener la rapidez en el punto B.

a) La definición de potencial eléctrico para una carga puntual es:

\begin{equation*}
V=\frac{1}{4\pi\epsilon_0}\frac{q}{r},
\end{equation*}

[mepr-show rules=”4409″ unauth=”both”]

donde en A el potencial eléctrico total es solo la suma de cada una de las cargas. Entonces:

\begin{equation*}
V_A=\frac{1}{4\pi\epsilon_0}\frac{q_1}{r_{1A}}+\frac{1}{4\pi\epsilon_0}\frac{q_2}{r_{2A}},
\end{equation*}

que, con valores numéricos, nos da:

\begin{equation*}
V_A \approx 2.56 \times 10^{4} \, \text{J/C}.
\end{equation*}

b) En el punto B se aplica el mismo análisis:

\begin{equation*}
V_B=\frac{1}{4\pi\epsilon_0}\frac{q_1}{r_{1B}}+\frac{1}{4\pi\epsilon_0}\frac{q_2}{r_{2B}},
\end{equation*}

que con valores numéricos es:

\begin{equation*}
V_B \approx 2.78 \times 10^{4} \, \text{J/C}.
\end{equation*}

c) Por conservación de energía:

\begin{equation*}
U_A + K_A = U_B + K_B.
\end{equation*}

Usando el hecho de que \(U= qV\) y \(K = \frac{1}{2}mv^2 \), luego:

\begin{equation*}
qV_A + \frac{1}{2}mv_A^2 = qV_B + \frac{1}{2}mv_B^2,
\end{equation*}

donde despejando \(v_B \) obtenemos:

\begin{equation*}
v_B=\sqrt{\frac{2q}{m}(V_A-V_B)+v_A^2},
\end{equation*}

que con valores numéricos es:

\begin{equation*}
v_B \approx 2.78 \times 10^{7} \, \text{m/s}.
\end{equation*}

Para obtener una explicación más detallada de cualquiera de estos pasos, haga clic en “Solución detallada”.

[/mepr-show]

Para las dos primeras preguntas, necesitamos encontrar el potencial eléctrico en los puntos \(A \) y \(B \). La estrategia que seguiremos es utilizar la definición del potencial eléctrico para cargas puntuales y el principio de superposición.

a) Comencemos recordando la definición de potencial eléctrico para una carga puntual

\begin{equation}
\label{potelec}
V=\frac{1}{4\pi\epsilon_0}\frac{q}{r},
\end{equation}

[mepr-show rules=”4409″ unauth=”both”]

donde \(q \) es la magnitud de la carga, \(r \) es la distancia desde la carga hasta el punto donde queremos calcular el potencial eléctrico, y \(\epsilon_0 \) es la permitividad del vacío, una constante física. Observe que el potencial eléctrico es una cantidad escalar, no vectorial. Para encontrar el potencial eléctrico en \(A\) \((V_A)\), podemos usar el principio de superposición, es decir, el potencial eléctrico en \(A \) es igual a la suma del potencial eléctrico debido a las cargas \(q_1\) \((V_1)\) y \(q_2\) \((V_2)\); explícitamente,

\begin{equation}
\label{va}
V_A=V_1+V_2.
\end{equation}

Comenzamos calculando \(V_1 \) usando la ecuación \eqref{potelec}

\begin{equation}
\label{v1}
V_1=\frac{1}{4\pi\epsilon_0}\frac{q_1}{r_{1A}},
\end{equation}

donde \(r_{1A} \) es la distancia entre la carga \(q_1 \) y el punto \(A \), según el enunciado esta distancia es \begin{equation}
r_{1A}=0.5\,\text{m}.
\end{equation}

Podemos hacer lo mismo con la carga \(q_2 \) y obtener la expresión

\begin{equation}
\label{v2}
V_2=\frac{1}{4\pi\epsilon_0}\frac{q_2}{r_{2A}},
\end{equation}

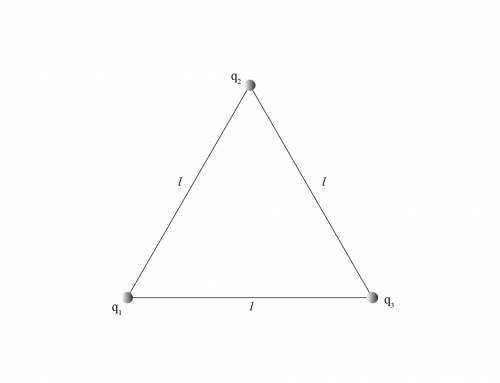
donde \(r_{2A} \) es la distancia entre la carga \(q_2 \) y el punto \(A \), que se puede encontrar usando geometría, específicamente, el teorema de Pitágoras, como se ve en la figura 1.

Figura 1: Distancias medidas desde las cargas a los puntos A y B.

Luego,
\begin{equation}
r_{2A}=\sqrt{(1\,\text{m})^2+(0.5\,\text{m})^2}\approx1.12\,\text{m}.
\end{equation}
Usando las ecuaciones \eqref{v1} y \eqref{v2} en la ecuación \eqref{va} finalmente obtenemos

\begin{equation}
\label{va2}
V_A=\frac{1}{4\pi\epsilon_0}\frac{q_1}{r_{1A}}+\frac{1}{4\pi\epsilon_0}\frac{q_2}{r_{2A}},
\end{equation}

donde podemos factorizar una parte del término \(\frac{1} {4 \pi \epsilon_0} \) para simplificar la expresión en \eqref{va2} a

\begin{equation}
\label{va2fac}
V_A=\frac{1}{4\pi\epsilon_0}\left(\frac{q_1}{r_{1A}}+\frac{q_2}{r_{2A}}\right)
\end{equation}

que numéricamente es

\begin{equation}
V_A=\frac{1}{4\pi (8.854\times 10^{-12}\, \text{C}^2/\text{N m}^2)}\left(\frac{5\times10^{-6}\,\text{C}}{0.5\,\text{m}}+\frac{(-8\,\times 10^{-6}\,\text{C})}{1.12\,\text{m}}\right),
\end{equation}

\begin{equation}
V_A\approx 2.56\times 10^{4}\,\text{J}/\text{C}.
\end{equation}

b) Para calcular el potencial eléctrico en \(B \), podemos hacer el mismo análisis realizado en la parte (a) y obtener una ecuación similar a la de \eqref{va2fac}; a saber,

\begin{equation}
\label{vb}
V_B=\dfrac{1}{4\pi\epsilon_0}\left(\frac{q_1}{r_{1B}}+\frac{q_2}{r_{2B}}\right),
\end{equation}

donde \(r_{1B} \) y \(r_{2B} \) son las distancias entre el punto \(B \) y las cargas \(q_1 \) y \(q_2 \), respectivamente. Estas distancias vienen dadas por el enunciado \(r_{1B} = 0.4 \, \text{m} \) y \(r_{2B} = 0.85 \text{m} \); porlo tanto, podemos calcular explícitamente el potencial eléctrico en \(B \) siguiendo la ecuación \eqref{vb}

\begin{equation}
V_B=\frac{1}{4\pi (8.854\times 10^{-12}\, \text{C}^2/\text{N m}^2)}\left(\frac{5\times10^{-6}\,\text{C}}{0.4\,\text{m}}+\frac{(-8\,\times 10^{-6}\,\text{C})}{0.85\,\text{m}}\right),
\end{equation}

\begin{equation}
V_B\approx2.78\times 10^{4}\,\text{J}/\text{C}.
\end{equation}

c) Ahora, consideremos un electrón que viaja de \(B \) a \(A \). Dado que llega a \(A \) con una rapidez de 820 m/s, necesitamos encontrar la rapidez que tenía en \(B \). En esta parte del problema, usaremos la relación entre el potencial eléctrico y la energía potencial eléctrica para luego usar el principio de conservación de energía. Ya que tenemos el potencial eléctrico en los puntos \(A \) y \(B \) y conocemos la carga de la partícula que se mueve entre estos puntos, podemos calcular la energía potencial eléctrica \(U \) usando la relación

\begin{equation}
\label{potential}
U=qV,
\end{equation}

donde \(q \) en nuestro caso es la carga del electrón, a saber, \(q = -1.602 \times 10^{-19} \,\text{C} \). Entonces, podemos usar el hecho de que que la energía mecánica de la partícula se conserva porque no hay fuerzas disipativas (como la fricción) que actúen sobre la partícula; por lo tanto, la suma de todos los tipos de energía potencial más la energía cinética \(K \) debe conservarse; explícitamente:

\begin{equation}
\label{conservation}
U_A+K_A=U_B+K_B,
\end{equation}

donde \(U_A \) y \(K_A \) son la energía potencial eléctrica y la energía cinética en el punto \(A \), respectivamente, y \(U_B \) y \(K_B \) son la energía potencial eléctrica y la energía cinética en el punto \(B \). Ahora podemos usar la expresión para la energía cinética

\begin{equation}
\label{kinetic}
K=\frac{1}{2}mv^2,
\end{equation}

donde \(m \) es la masa y \(v \) es la rapidez . Usando la definición de la ecuación \eqref{kinetic} en la ecuación \eqref{conservation}, obtenemos

\begin{equation}
\label{cons2}
U_A+\frac{1}{2}mv_A^2=U_B+\frac{1}{2}mv_B^2.
\end{equation}

Ahora, usamos la definición de energía potencial dada en la ecuación \eqref{potential} en la ecuación \eqref{cons2} para obtener

\begin{equation}
qV_A+\frac{1}{2}mv_A^2=qV_B+\frac{1}{2}mv_B^2,
\end{equation}

donde la única variable desconocida es \(v_B \). Despejando \(v_B \), obtenemos

\begin{equation}
\frac{1}{2}mv_B^2=qV_A-qV_B+\frac{1}{2}mv_A^2,
\end{equation}

y luego multiplicando por \( 2/m \), obtenemos

\begin{equation}
v_B^2=\frac{2}{m}\left(qV_A-qV_B+\frac{1}{2}mv_A^2\right),
\end{equation}

que es equivalente a

\begin{equation}
v_B^2=\frac{2q}{m}(V_A-V_B)+v_A^2.
\end{equation}

Finalmente, sacando la raíz cuadrada en ambos lados:

\begin{equation}
v_B=\sqrt{\frac{2q}{m}(V_A-V_B)+v_A^2}.
\end{equation}

Usando los valores numéricos dados y los calculados en partes anteriores del problema, obtenemos

\begin{equation*}
v_B=\sqrt{\frac{2(-1.602\times 10^{-19}\,\text{C})(2.57\times 10^{4}\,\text{J}/\text{C}-2.78\times 10^{4}\,\text{J}/\text{C}}{(9.11\times 10^{-31}\,\text{kg})}+(820\,\text{m}/\text{s})^2)},
\end{equation*}

\begin{equation}
v_B\approx 2.78 \times 10^7\,\text{m}/\text{s}.
\end{equation}

¡Esto significa que el electrón redujo su rapidez en 5 órdenes de magnitud!

[/mepr-show]

You need to be registered and logged in to take this quiz. Log in