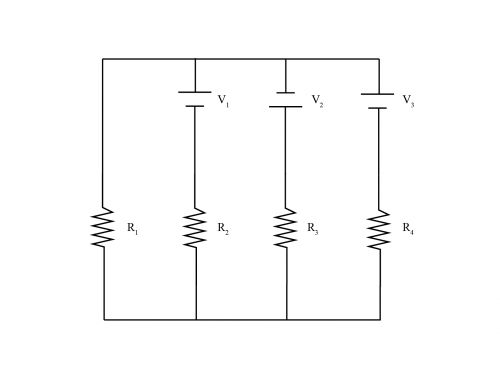
Un circuito como el que se muestra en la figura tiene las siguientes baterías: \ \( V_1 = 15 \, \ text{V} \) y \ \( V_2 = 20 \, \ text{V} \). Las resistencias son \ \( R_1 = 50 \, \ Omega \), \ \( R_2 = 100 \, \ Omega \), \ \( R_3 = 70 \, \ Omega \), \ \( R_4 = 80 \, \ Omega \) y \ \( R_5 = 60 \, \ Omega \). Sobre la resistencia \ \( R_3 \):
a) ¿Cuánta corriente fluye y en qué dirección?
b) Calcule la caída de voltaje.
c) ¿Cuánta potencia se disipa?
a) Suponiendo que la dirección de la corriente está determinada por la batería, aplique la ley de Kirchhoff y la ley de Ohm para obtener la relación necesaria para resolver la corriente.
b) Dado que ya se conoce la corriente, aplique la ley de Ohm para resolver la caída de voltaje.
c) Con las variables de corriente y voltaje ya encontradas, la potencia se puede calcular fácilmente.
a) Podemos escribir:
\begin{equation*}
\ sum V_{up} = \ suma V_{down} .
\end{equation*}
[mepr-show rules=”4409″ unauth=”both”]
Para \ \( I_1 \), y aplicando la ley de Ohm para cada voltaje:
\begin{equation*}
V_1 = I_1 R_1 + (I_1 + I_2) R_3 + I_1 R_4.
\end{equation*}
Para \ \( I_2 \), y también aplicando la Ley de Ohm para cada voltaje:
\begin{equation*}
V_2 = I_2 R_2 + (I_2 + I_1) R_3 + I_2 R_5.
\end{equation*}
Para ambas ecuaciones \ \( I_1 \) y \ \( I_2 \) son las variables desconocidas. Resolviendo el sistema \ \( 2 \ times 2 \) obtenemos:
\begin{equation*}
I_1 \ aproximadamente 0.050 \, \ text{A} ,
\end{equation*}
y
\begin{equation*}
I_2 \ aproximadamente 0.072 \, \ text{A} ,
\end{equation*}
La corriente que fluye a través de la resistencia \ \( R_3 \) es:
\begin{equation*}
I_1 + I_2 \ aproximadamente 0.122 \, \ text{A} .
\end{equation*}
b) La caída de voltaje en \ \( R_3 \) se puede calcular con la ley de Ohm con la \( I_1 + I_2 \). Entonces
\begin{equation}
V_3 \ approx -8.54 \, \ text{V} .
\end{equation}
c) La potencia disipada por \ \( R_3 \) se puede calcular mediante \ \( P = IV \). Numéricamente:
\begin{equation}
P_3 \ approx -1.04 \, \ text{W} .
\end{equation}
Para obtener una explicación más detallada de cualquiera de estos pasos, haga clic en “Solución detallada”.
[/mepr-show]
a) Nos piden que encontremos la magnitud y la dirección de la corriente en \ \( R_3 \). Para resolver este problema debemos utilizar las leyes de Kirchhoff. La ley de voltaje de Kirchhoff indica que en un camino cerrado la suma de voltajes \ \( V_i \) debe ser igual a cero, explícitamente
\begin{equation}
\label{kirch}
\ sum _ {\ text {ruta cerrada}} V_i = 0
\end{equation}
[mepr-show rules=”4409″ unauth=”both”]
Lo primero que tendremos que hacer es elegir los caminos cerrados que cubren todo el circuito y su orientación. Luego, para cada ruta asignaremos una \ \( I \) actual. Ver figura 1.
Figura 1: Para aplicar la ley de voltaje de Kirchhoff, usamos dos caminos cerrados con corrientes \ \( I_1 \) y \ \( I_2 \). Observe que la corriente \ \( I_1 \) fluye en sentido horario, mientras que la corriente \ \( I_2 \) fluye en sentido antihorario. Los caminos son tales que la corriente va desde los terminales negativos a los positivos de la fuente de voltaje respectiva.
Centrémonos primero en el camino cerrado de la izquierda, asignamos el \ \( I_1 \) actual a este camino. La ruta pasa por 4 elementos: fuente \ \( V_1 \) y resistencias \ \( R_1 \), \ \( R_3 \) y \ \( R_4 \), entonces debemos tener 4 términos en la ley de voltaje de Kirchhoff, explícitamente, usando la ecuación \ eqref{kirch}
\begin{equation}
\label{malla1}
V_{V_1} + V_{R_1} + V_{R_3} + V_{R_4} = 0.
\end{equation}
Para calcular el voltaje de una fuente, la dirección en la que se toma el camino es fundamental: si el camino se toma del terminal negativo al positivo de la fuente de voltaje, entonces \ \( V_{V_1}= + V_{1}\), si la ruta se toma en la dirección del terminal positivo al negativo de la fuente de voltaje, entonces \ \( V_{V_1}= -V_{1}\).
Para una resistencia, siempre hay una caída de voltaje en la dirección de la corriente, luego, de acuerdo con la ley de Ohm, podemos escribir
\begin{equation}
\label{ohm}
V_{R} = -IR,
\end{equation}
donde \ \( I \) es la corriente total que pasa a través de la resistencia y se toma positiva en la dirección de la ruta y negativa en la dirección opuesta a la ruta. Luego, usando la ecuación \ eqref{ohm} tenemos
\begin{equation}
V_{R_1} = -I_1R_1,
\end{equation}
\begin{equation}
V_{R_4} = -I_1R_4.
\end{equation}
Observe que a través del resistor \ \( R_3 \) la corriente total será \ \( I_1 + I_2 \), entonces
\begin{equation}
\label{v3}
V_{R_3} = – (I_1 + I_2) R_3.
\end{equation}
Poniendo los resultados anteriores en la ecuación \ eqref{malla1} obtenemos nuestra primera ecuación para resolver todo el sistema, a saber
\begin{equation}
\label{ec1}
V_1-I_1R_1- (I_1 + I_2) R_3-I_1R_4 = 0.
\end{equation}
Después de alguna manipulación algebraica, la ecuación \ eqref{ec1} Se puede escribir como
\begin{equation}
\ label {ec1.1}
V_1 = I_1 (R_1 + R_3 + R_4) + I_2R_3
\end{equation}
Ahora centrémonos en el camino de la derecha. También tiene cuatro elementos: fuente \ \( V_2 \) y resistencias \ \( R_2 \), \ \( R_3 \) y \ \( R_5 \). Entonces debemos tener 4 términos en la ley de voltaje de Kirchhoff. Explícitamente, usando la ecuación \ eqref{kirch}
\begin{equation}
\label{malla2}
V_{V_2} + V_{R_2} + V_{R_3} + V_{R_5} = 0.
\end{equation}
Usando el mismo argumento que antes podemos decir que
\begin{equation}
V_{V_2} = V_2,
\end{equation}
porque el camino fluye desde el terminal negativo al positivo de la fuente. Usando la ecuación \ eqref{ohm} tenemos
\begin{equation}
V_{R_2} = -I_2R_2,
\end{equation}
\begin{equation}
V_{R_5} = -I_2R_5.
\end{equation}
Observe que a través del resistor \ \( R_3 \) la corriente total será \ \( I_1 + I_2 \), entonces
\begin{equation}
V_{R_3} = – (I_1 + I_2) R_3,
\end{equation}
las corrientes \ \( I_1 \) y \ \( I_2 \) se toman positivas ya que van en la misma dirección definida por la ruta.
Poniendo los resultados anteriores en la ecuación \ eqref{malla2} obtenemos nuestra segunda ecuación para resolver todo el sistema, a saber
\begin{equation}
\label{ec2}
V_2-I_2R_2- (I_1 + I_2) R_3-I_1R_5 = 0.
\end{equation}
Después de una reorganización de los términos en la ecuación \ eqref{ec2} se puede escribir como
\begin{equation}
\ label {ec2.1}
V_2 = I_2 (R_2 + R_3 + R_5) + I_1R_3.
\end{equation}
Ahora tenemos un problema de álgebra: dos ecuaciones \( \ eqref {ec1.1} y \ eqref {ec2.1}) con dos incógnitas \( \ \( I_1 \) y \ \( I_2 \)). Resolviendo para \ \( I_2 \) en la ecuación \ eqref {ec2.1} obtenemos
\begin{equation}
\label{I_2}
I_2 = \ frac{V_2-I_1R_3} {R_2 + R_3 + R_5}.
\end{equation}
Usando la expresión para \ \( I_2 \) dada en la ecuación \ eqref{I_2} en la ecuación \ eqref {ec1.1} obtenemos
\begin{equation}
V_1 = I_1 (R_1 + R_3 + R_4) + \ izquierda (\ frac{V_2-I_1R_3} {R_2 + R_3 + R_5} \ derecha) R_3.
\end{equation}
Expandiendo el segundo término en la expresión anterior obtenemos
\begin{equation}
\label{i12}
V_1 = I_1 (R_1 + R_3 + R_4) + \ frac{V_2R_3} {R_2 + R_3 + R_5} – \ frac {I_1R_3 ^ 2} {R_2 + R_3 + R_5}.
\end{equation}
Tomando los términos no multiplicados por \ \( I_1 \) al lado izquierdo de la ecuación y factorizando \ \( I_1 \) en el lado derecho obtenemos
\begin{equation}
\label{i111}
V_1- \ frac{V_2R_3} {R_2 + R_3 + R_5} = I_1 \ left (R_1 + R_3 + R_4- \ frac {R_3 ^ 2} {R_2 + R_3 + R_5} \ right).
\end{equation}
Resolviendo \ \( I_1 \) en la ecuación \ eqref{i111} finalmente conseguimos
\begin{equation}
I_1 = \ frac {V_1- \ frac{V_2R_3} {R_2 + R_3 + R_5}} {R_1 + R_3 + R_4- \ frac {R_3 ^ 2} {R_2 + R_3 + R_5}}.
\end{equation}
Usando los valores numéricos para cada resistor y las fuentes de voltaje obtenemos
\begin{equation}
I_1 = \ frac {15 \, \ text{V} – \ frac {(20 \, \ text{V} ) (70 \, \ Omega)} {100 \, \ Omega + 70 \, \ Omega + 60 \, \ Omega}} {50 \, \ Omega + 70 \, \ Omega + 80 \, \ Omega- \ frac {(70 \, \ Omega) ^ 2} {100 \, \ Omega + 70 \, \ Omega + 60 \, \ Omega}},
\end{equation}
luego
\begin{equation}
I_1 \ aproximadamente 0.050 \, \ text{A} .
\end{equation}
Ahora, usando la ecuación \ eqref{I_2} podemos calcular \ \( I_2 \) para ser
\begin{equation}
I_2 = \ frac {(20 \, \ text{V} ) – (0.050 \, \ texto{A} ) (70 \, \ Omega)} {100 \, \ Omega + 70 \, \ Omega + 60 \, \ Omega},
\end{equation}
luego
\begin{equation}
I_2 \ approx0.072 \, \ text{A} .
\end{equation}
Entonces la corriente que fluye a través de la resistencia \ \( R_3 \) es
\begin{equation}
I_1 + I_2 = 0.050 \, \ text{A} +0.072 \, \ texto{A} = 0,122 \, \ texto{A} .
\end{equation}
b) La caída de voltaje en \ \( R_3 \) se puede calcular con la ecuación \ eqref{v3} , explícitamente
\begin{equation}
V_3 = – (0.050 \, \ text{A} +0.072 \, \ texto{A} ) (70 \, \ Omega) \ approx -8.54 \, \ text{V} .
\end{equation}
c) La potencia disipada por \ \( R_3 \), a saber \ \( P \), se puede calcular de acuerdo con la ecuación
\begin{equation}
P = VI.
\end{equation}
En nuestro caso particular, este poder es
\begin{equation}
P_3 = V_3 (I_1 + I_2),
\end{equation}
que numéricamente es
\begin{equation}
P_3 = (- 8.54 \, \ texto{V} ) (0,122 \, \ texto{A} ) = – 1.04 \, \ text{W} .
\end{equation}
El signo menos indica que la resistencia está disipando energía en forma de calor. Las unidades son Watts, lo que equivale a Julios por segundo.
[/mepr-show]
You need to be registered and logged in to take this quiz. Log in




Leave A Comment