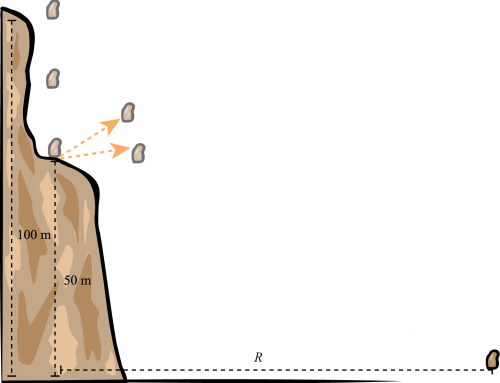
Una arquera aficionada quiere golpear una manzana e ingenuamente le apunta directamente, como se muestra en la imagen. Un golpe de suerte la beneficia porque una ráfaga de viento golpea fortuitamente la manzana de la rama del árbol justo después de que se suelta la flecha.
(a) Muestre que la flecha siempre perforará la manzana mientras sople el viento, siempre que la arquera apunte exactamente hacia ella mientras suelta la flecha.
(b) ¿Por qué es una arquera aficionada? ¿En qué dirección se debería apuntar el arco y la flecha, suponiendo que haya menos viento en el futuro?
a) Considere que las posiciones verticales serán las mismas. Luego, encuentre cada posición vertical con la ecuación de movimiento de un objeto que se mueve con aceleración constante.
b) A la arquera le falta una variable importante que afecta el movimiento de cualquier objeto que cae.
a) Usando la ecuación de movimiento para un objeto que se mueve con rapidez constante, tenemos:
\begin{equation*}
x= v_x t,
\end{equation*}
donde \(v_x = v_i \cos \theta\) y \(x = L\). Despejando \(t\), obtenemos:
\begin{equation*}
t=\frac{L}{v_i\cos(\theta)}.
\end{equation*}
Para un objeto que cae, la ecuación de movimiento es:
\begin{equation*}
y_f = y_i + v_{i} t – \frac{1}{2} gt^2.
\end{equation*}
Si la flecha golpea la manzana, sus posiciones finales deben ser las mismas ( \( y_a = y_f \)). Entonces, por las condiciones dadas obtenemos
\begin{equation*}
v_i\sin(\theta) t-\frac{1}{2}gt^2=H-\frac{1}{2}gt^2.
\end{equation*}
Usando el tiempo \( t \) encontrado antes, y después de usar algo de álgebra, obtenemos la condición para que la flecha golpee la manzana:
\begin{equation*}
\tan(\theta)=\frac{H}{L}.
\end{equation*}
b) La arquera es una aficionada porque no está tomando en cuenta los efectos de la gravedad en el tiro. Si los fuertes vientos no hubieran derribado la manzana, nunca hubiera podido perforarla apuntándola directamente. Un arquero más experimentado tendría en cuenta la gravedad y apuntaría un poco más alto.
Para obtener una explicación más detallada de cualquiera de estos pasos, haga clic en “Solución detallada”.
(a) Nos han pedido que demostremos que mientras la arquera apunte directamente a la manzana, la flecha siempre la golpeará si comienza a caer al mismo tiempo que se suelta la flecha. Comencemos por hacer un bosquejo de la situación (ver figura 1).
Figura 1: Colocamos el sistema de coordenadas en la posición inicial de la flecha. La distancia vertical desde la flecha hasta la fruta es inicialmente \( H \), mientras que la distancia horizontal entre la flecha y la fruta es \( L \). También se muestra el ángulo \(\theta\).
Vemos que la flecha está inicialmente a una distancia \( L \) a lo largo del eje X, y la distancia vertical entre la posición inicial de la manzana y la posición inicial de la flecha es \( H \). Luego, escribamos las ecuaciones de movimiento a lo largo de los ejes X y Y para la flecha y para la manzana y busquemos una condición para que la flecha golpee la fruta.
Primero, observe que la flecha sigue el movimiento de un proyectil. Por lo tanto, a lo largo del eje X, la velocidad es positiva y constante, por lo que la ecuación de movimiento es
\begin{equation}
\label{xa0}
x_a\,\hat{\textbf{i}}=x_{i,a}\,\hat{\textbf{i}}+v_{xi} t\,\hat{\textbf{i}},
\end{equation}
donde \(x_{i,a}=0\) es la posición inicial de la flecha, \(v_{xi}\) es la rapidez inicial a lo largo de X, y \( x_a \) es la posición final en X. Ahora, observe que \( v_{xi}= v_i\cos(\theta) \) es la velocidad inicial a lo largo del eje X, donde \(\theta\) es el ángulo con respecto a la línea horizontal a la que apunta el arquero. Esto se ilustra en la figura 2.
Figura 2: La velocidad inicial de la flecha \( \vec{v} _i \) tiene componentes a lo largo de los ejes X y Y, como se muestra aquí. Su dirección está dada por el ángulo \(\theta\).
Por tanto, \eqref{xa0} se convierte en
\begin{equation}
\label{xa}
x_a\,\hat{\textbf{i}}=x_{i,a}\,\hat{\textbf{i}}+v_i\cos(\theta) t\,\hat{\textbf{i}}.
\end{equation}
Podemos eliminar la notación vectorial y centrarnos en las magnitudes para obtener
\begin{equation}
x_a=v_i\cos(\theta) t,
\end{equation}
donde ya hemos utilizado el hecho de que \(x_ {i,a}=0\). Dado que la manzana cae y no cambia su posición en el eje X, el único punto a lo largo de este eje donde la flecha y la manzana pueden encontrarse es en \( x = L \). Por lo tanto, establecemos \( x_a = L \) en la ecuación anterior y despejamos el tiempo \( t \), que es el tiempo que tarda la flecha en viajar desde el arquero hasta el punto en el eje X donde cae la manzana. Explícitamente,
\begin{equation}
L=v_i\cos(\theta)t,
\end{equation}
y despejando el tiempo, obtenemos
\begin{equation}
\label{time}
t=\frac{L}{v_i\cos(\theta)}.
\end{equation}
Hemos encontrado una expresión para el tiempo en términos del ángulo y la rapidez inicial (que no conocemos). Al final del día, en realidad necesitamos encontrar este ángulo (por lo que mostramos que la dirección es la que nos dijeron en el enunciado). Entonces necesitamos más ecuaciones.
Centrémonos en el movimiento a lo largo del eje Y. En el eje Y, la flecha cae con aceleración gravitacional constante negativa, por lo que la ecuación de movimiento a lo largo de Y dice:
\begin{equation}
y_a\,\hat{\textbf{j}}=y_{i,a}\,\hat{\textbf{j}}+v_{yi}\,\hat{\textbf{j}}-\frac{1}{2}gt^2\,\hat{\textbf{j}},
\end{equation}
donde \(y_ {i,a}=0\) es la posición inicial de la flecha y \(v_{yi}\) es la rapidez vertical inicial. Ahora, en la figura 2, vemos que \(v_{yi}=v_i\sin(\theta)\) es la velocidad inicial a lo largo del eje Y, donde el ángulo \(\theta\) se define como antes y \(g=9.8\,\text{m/s}^2\) es la aceleración gravitacional de la Tierra. Por lo tanto, obtenemos
\begin{equation}
y_a\,\hat{\textbf{j}}=y_{i,a}\,\hat{\textbf{j}}+v_i\sin(\theta)\,\hat{\textbf{j}}-\frac{1}{2}gt^2\,\hat{\textbf{j}}.
\end{equation}
Centrándonos en las magnitudes (eliminando la notación vectorial), obtenemos
\begin{equation}
\label{ya}
y_a=v_{i}\sin(\theta)-\frac{1}{2}gt^2,
\end{equation}
donde usamos el hecho de que, según el sistema de coordenadas, \(y_{i,a}=0\). Nuevamente, tenemos una ecuación que involucra tres variables desconocidas: el ángulo inicial, el tiempo y la rapidez inicial. Entonces, para encontrar el ángulo, necesitamos al menos una ecuación más.
Para que la flecha golpee la manzana, sus posiciones Y deben ser las mismas en el mismo momento exacto. Entonces, considere la ecuación de movimiento de la manzana. La fruta cae con aceleración gravitacional constante, por lo que la ecuación de movimiento es
\begin{equation}
y_f\,\hat{\textbf{j}}=y_{i,f}\,\hat{\textbf{j}}+v_{i,f}\,\hat{\textbf{j}}-\frac{1}{2}gt^2\,\hat{\textbf{j}},
\end{equation}
donde \(y_{i,f}=H\) es la posición inicial de la fruta y \(v_{i,f}=0\) es la velocidad inicial a lo largo del eje Y, que es cero. Entonces podemos escribir la ecuación de movimiento de la manzana como
\begin{equation}
y_f\,\hat{\textbf{j}}=H\,\hat{\textbf{j}}-\frac{1}{2}gt^2\,\hat{\textbf{j}},
\end{equation}
o, después de eliminar la notación vectorial, como
\begin{equation}
\label{yf}
y_f=H-\frac{1}{2}gt^2.
\end{equation}
Observe que el tiempo \( t = 0 \) aquí se considera que es el momento en que la flecha sale del arco y la manzana comienza a caer debido al fuerte viento.
Como explicamos anteriormente, si la flecha golpea la manzana, sus posiciones finales deben ser las mismas. Ya dijimos que la posición de la flecha a lo largo del eje X es la misma que la de la fruta, es decir, \( x_a = L \). Y para el eje Y, decimos que
\begin{equation}
y_a=y_f.
\end{equation}
Usando las expresiones explícitas dadas por las ecuaciones \eqref{ya} y \eqref{yf} en esta ecuación, obtenemos
\begin{equation}
v_i\sin(\theta) t-\frac{1}{2}gt^2=H-\frac{1}{2}gt^2,
\end{equation}
donde podemos cancelar el término \(\frac{1}{2}gt^2\) y obtener
\begin{equation}
v_i\sin(\theta) t=H.
\end{equation}
Usando la expresión para el tiempo que tarda la flecha en viajar al punto \( x_a = L \), dado por la ecuación \eqref{time}, podemos escribir esta expresión como
\begin{equation}
v_i\sin(\theta)\left(\frac{L}{v_i \cos(\theta)}\right)=H.
\end{equation}
Esto simplifica a
\begin{equation}
L\tan(\theta)=H.
\end{equation}
Por lo tanto, la condición para que la flecha golpee la fruta es que el ángulo \(\theta\), al que apunta la arquera, sea tal que
\begin{equation}
\tan(\theta)=\frac{H}{L}.
\end{equation}
Un dibujo que ilustre esto podría ser útil. Ver figura 3.
Figura 3: El ángulo \(\theta\) se forma en el triángulo definido por \(H\) y \(L\).
Como vemos en el dibujo, esta condición se logra si el arquero apunta directamente a la manzana, tal y como el enunciado nos pidió que mostráramos. A partir de este dibujo y trigonometría básica, encontramos que si el arquero apunta directamente a la manzana, entonces
\begin{equation}
\tan(\theta)=\frac{H}{L}.
\end{equation}
Esto es cierto siempre que la velocidad inicial sea suficiente para que la flecha recorra la distancia \(L\) horizontalmente.
(b) Es una arquera aficionada porque no tiene en cuenta los efectos de la gravedad en su tiro. Si los fuertes vientos no hubieran derribado la manzana, nunca habría podido perforarla apuntándola directamente.
Un arquero más experimentado tendría en cuenta la gravedad y apuntaría un poco más alto. Ver figura 4.
Figura 4: Si la fruta no cae al mismo tiempo que la flecha sale del arco, entonces el arquero no perfora la fruta si la apunta directamente.
You need to be registered and logged in to take this quiz. Log in



Leave A Comment