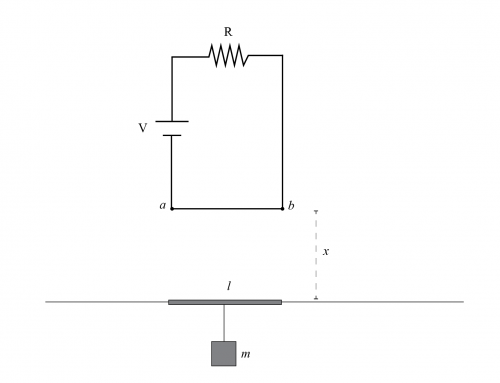
Considere una región donde hay un campo magnético de 1.4 T entrando a la pantalla. Perpendicular a él (sobre la pantalla), hay un circuito con una resistencia de \(15 \Omega \). La barra que cierra el circuito tiene 40 cm de largo y se mueve sobre rieles sin fricción hacia la derecha a una rapidez de 25 m/s, como se muestra en la figura. Suponga que la barra tiene una resistencia despreciable.
(a) Encuentre la fem inducida en el circuito.
(b) Encuentre la corriente inducida en el circuito.
(c) Si queremos que la barra se mueva con rapidez constante, ¿cuánta fuerza se debe aplicar a la barra y en qué dirección?
a) Utilice la definición de fem inducida por el flujo magnético. Para el área, las dimensiones se pueden relacionar con la velocidad.
b) Con la fem inducida, use la ley de Ohm para obtener la corriente.
c) Encuentre la fuerza magnética y use la segunda ley de Newton.
a) La Ley de Faraday establece:
\begin{equation*}
\mathcal{E}=-\frac{d\Phi_B}{dt},
\end{equation*}
[mepr-show rules=”4409″ unauth=”both”]
donde el flujo magnético es:
\begin{equation*}
\Phi_B=-BA.
\end{equation*}
Dado que el área es \(A = \ell x \), entonces:
\begin{equation*}
\mathcal{E} = – \frac{d\Phi_B}{dt}= B\ell \frac{dx}{dt},
\end{equation*}
donde \(\frac{dx}{dt} = v \). Entonces:
\begin{equation*}
\mathcal{E}=B\ell v,
\end{equation*}
que numéricamente es
\begin{equation*}
\mathcal{E}=14\,\text{V}.
\end{equation*}
b) De la ley de Ohm, despejando \(I \) y reemplazando el valor encontrado para \(\mathcal{E} \) obtenemos:
\begin{equation*}
I=\frac{B \ell v}{R},
\end{equation*}
o
\begin{equation*}
I \approx 0.93 \, \text{A}.
\end{equation*}
c) Dado que la fuerza magnética es \(\vec{F} = I \vec{L} \times \vec{B} \), luego:
\begin{equation*}
\vec{F}_B=-ILB\,\hat{\textbf{i}},
\end{equation*}
lo que significa que la fuerza se dirige hacia la izquierda. Según la segunda ley de Newton para el movimiento con velocidad constante, tenemos:
\begin{equation*}
F – F_B = 0.
\end{equation*}
Entonces:
\begin{equation*}
F = ILB,
\end{equation*}
o:
\begin{equation*}
F \approx 0.52 \, \text{N}.
\end{equation*}
Para obtener una explicación más detallada de cualquiera de estos pasos, haga clic en “Solución detallada”.
[/mepr-show]
a) Debemos encontrar la fuerza electromotriz inducida en el circuito. Para resolver este problema, usaremos la ley de inducción de Faraday para encontrar la fem \(\mathcal{E} \) calculando el cambio en el flujo magnético \(\Phi_B \). La ley de Faraday establece que
\begin{equation}
\label{fem}
\mathcal{E}=-\frac{d\Phi_B}{dt},
\end{equation}
[mepr-show rules=”4409″ unauth=”both”]
donde el flujo magnético \(\Phi_B \) sobre una superficie dada se define como
\begin{equation}
\label{flujomag}
\Phi_B=\int_S \vec{B}\cdot \hat{\textbf{n}} dA,
\end{equation}
donde \(\vec{B} \) es el campo magnético y \(\hat {\textbf{n} } \) es un vector unitario perpendicular a la superficie \(S \) en cada punto, y \(dA \) es el diferencial de área. Para una superficie plana como la del bucle y un campo magnético constante, la expresión en \eqref{flujomag} se simplifica a
\begin{equation}
\label{flujomag2}
\Phi_B=\int_S \vec{B}\cdot \hat{\textbf{n}} dA=\vec{B}\cdot \hat{\textbf{n}}\int_S dA,
\end{equation}
donde pudimos sacar el vector unitario y el campo magnético fuera de la integración porque son constantes (su magnitud y dirección son las mismas en toda la superficie). Por lo tanto, obtenemos
\begin{equation}
\label{fluxB}
\Phi_B=\vec{B}\cdot\hat{\textbf{n}}\, A,
\end{equation}
donde \(A \) es el área del bucle que está inmersa en el campo magnético. Podemos expresar esta área como
\begin{equation}
\label{arealoop}
A=\ell x,
\end{equation}
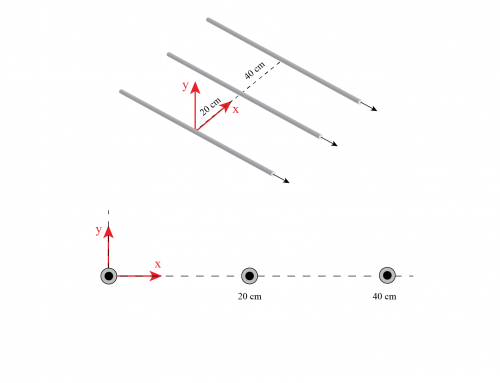
donde \(x \) es la distancia horizontal desde la resistencia a la barra en movimiento como se ve en la figura 1.
Figura 1: Bucle inmerso en una región de campo magnético constante que apunta a lo largo del eje Z negativo (entrando en la pantalla). La barra en movimiento tiene una velocidad \(\vec{v} \) y las dimensiones del bucle son \(l \) y \(x \). El vector unitario normal \(\hat {\textbf{n} } \), apuntando a lo largo del eje Z positivo, también se muestra. Observe el sistema de coordenadas que hemos elegido.
En la figura 1 vemos que el campo magnético se dirige hacia el eje Z negativo, por lo que podemos escribir
\begin{equation}
\label{bexplicit}
\vec{B}=-B\,\hat{\textbf{k}},
\end{equation}
donde \(B \) es la magnitud del campo magnético.
El vector unitario \(\hat {\textbf{n} } \) es perpendicular al plano XY, por lo que consideraremos que se dirige a lo largo del eje Z positivo, como se muestra en la figura 1 (también se puede dirigir hacia el eje Z negativo, pero por simplicidad elegiremos la dirección positiva). Por lo tanto, este vector unitario es idéntico a \(\hat {\textbf{k} } \):
\begin{equation}
\label{normalvec}
\hat{\textbf{n}}=\hat{\textbf{k}}.
\end{equation}
Usando esto y el resultado de la ecuación \eqref{bexplicit} en la ecuación \eqref{fluxB}, obtenemos
\begin{equation}
\label{flujoB2}
\Phi_B=(-B\,\hat{\textbf{k}})\cdot\hat{\textbf{k}}\,A=-BA,
\end{equation}
donde usamos el hecho de que \(\hat{\textbf{k}}\cdot\hat{\textbf{k}}=1\). Ahora, si usamos el resultado de la ecuación \eqref{arealoop} en esta ecuación, podemos escribir
\begin{equation}
\label{flujoB3}
\Phi_B=-B\ell x.
\end{equation}
Para encontrar la fuerza electromotriz inducida (fem), nos interesa la derivada temporal de la ecuación \eqref{flujoB3}:
\begin{equation}
\label{dtflujo}
\frac{d\Phi_B}{dt}=\frac{d(-B\ell x)}{dt}.
\end{equation}
Observe que \(B \) es constante, \(\ell \) es constante y solo \(x \) varía (a medida que se mueve la barra). Por tanto, podemos calcular la derivada temporal como
\begin{equation}
\label{dtflujo2}
\frac{d\Phi_B}{dt}=-B\ell \frac{dx}{dt}.
\end{equation}
La velocidad a la que \(x \) cambia en el tiempo, \(dx/dt \), es igual a la rapidez de la barra \(v \) en el eje X. Entonces, podemos reescribir \eqref{dtflujo2} como
\begin{equation}
\label{dtflujo3}
\frac{d\Phi_B}{dt}=-B\ell v.
\end{equation}
Usando este resultado en la ecuación \eqref{fem}, obtenemos
\begin{equation}
\label{ecfem}
\mathcal{E}=-(-B\ell v)=B\ell v,
\end{equation}
que numéricamente es
\begin{equation}
\mathcal{E}=(1.4\,\text{T})(0.4\,\text{m})(25\,\text{m/s})=14\,\text{V}.
\end{equation}
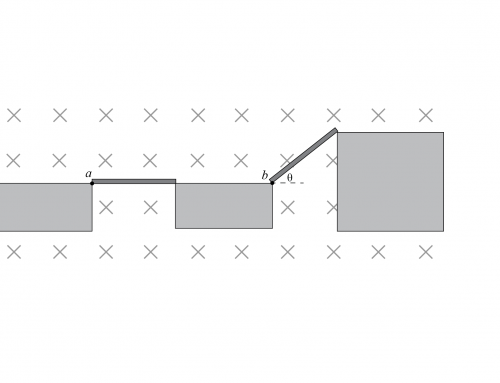
Observe que la fuerza electromotriz inducida es positiva. Por lo tanto, de acuerdo con la dirección del vector unitario \(\hat {\textbf{n} } \) y la regla de la mano derecha, esto significa que la corriente en el circuito se mueve en sentido antihorario. Para ver por qué, todo lo que tenemos que hacer es señalar con el pulgar de la mano derecha en la dirección del vector \(\hat {\textbf{n} } \); la dirección en la que se cierran los otros dedos define la dirección positiva de la corriente, como se muestra en la figura 2.
Figura 2: Debido a que la fem inducida es positiva, la dirección de la corriente viene dada por la regla de la mano derecha. Apuntando con el pulgar en la dirección de \(\hat {\textbf{n} } \), el resto de los dedos indican la dirección en la que fluye la corriente. Si la fem fuera negativa, entonces la corriente tendría la dirección opuesta.
Dado que \(\mathcal{E} \) es positiva, entonces la corriente que fluye a través de los bucles debido a la fuerza electromotriz se mueve en sentido antihorario.
b) Para encontrar la corriente inducida en el circuito, debemos usar la ley de Ohm
\begin{equation}
\label{ohm}
V=IR,
\end{equation}
donde \(V \) es el voltaje, \(I \) la corriente y \(R \) la resistencia. En nuestro caso, la fem es la misma que el voltaje. Entonces, despejando \(I \), obtenemos
\begin{equation}
I=\frac{V}{R},
\end{equation}
o, de manera equivalente,
\begin{equation}
I=\frac{\mathcal{E}}{R}.
\end{equation}
Usando aquí el resultado de la ecuación \eqref{ecfem}, finalmente obtenemos
\begin{equation}
I=\frac{B\ell v}{R},
\end{equation}
que numéricamente es
\begin{equation}
I=\frac{(1.4\,\text{T})(0.4\,\text{m})(25\,\text{m/s})}{15\,\Omega}\approx 0.93\,\text{A}.
\end{equation}
c) Para que la barra se mueva con velocidad constante, su aceleración debe ser cero. Por lo tanto, según la segunda ley de Newton, la suma de todas las fuerzas ejercidas sobre la barra a lo largo de la dirección X debe ser cero:
\begin{equation}
\sum_X \vec{F}=m\vec{a},
\end{equation}
\begin{equation}
\label{f0}
\sum_X \vec{F}=\vec{0}.
\end{equation}
Las dos fuerzas relevantes ejercidas sobre la barra a lo largo de la dirección X son la fuerza magnética \(\vec{F} _B \), y la fuerza que debemos aplicar para asegurarnos de que la barra se mueva con velocidad constante. La fuerza magnética está dada por la fuerza de Lorentz, que en ausencia de un campo eléctrico es
\begin{equation}
\label{lorentz}
\vec{F}_{B}=I\vec{L}\times\vec{B},
\end{equation}
donde \(I \) es la corriente, \(L \) es un vector cuya dirección es la misma que la corriente y su magnitud es la longitud de la barra.
De los puntos anteriores, conocemos la magnitud de la corriente inducida y su dirección, que es en sentido antihorario. Esto implica que para la barra en movimiento, la corriente se mueve hacia arriba, por lo que
\begin{equation}
\label{ele}
\vec{L}=L\,\hat{\textbf{j}},
\end{equation}
donde \(L=0.4\,\text{m}\). Luego, usando las expresiones dadas por \eqref{bexplicit} y \eqref{ele} en \eqref{lorentz}, vemos que la fuerza magnética ejercida sobre la barra es
\begin{equation}
\vec{F}_{B}=I(L\,\hat{\textbf{j}})\times(-B\,\hat{\textbf{k}}),
\end{equation}
\begin{equation}
\vec{F}_B=-ILB\,\hat{\textbf{j}}\times\hat{\textbf{k}},
\end{equation}
\begin{equation}
\label{fuerzamag}
\vec{F}_B=-ILB\,\hat{\textbf{i}},
\end{equation}
donde en la última línea usamos el hecho de que \(\hat {\textbf{j}}\times \hat {\textbf{k} } = \hat {\textbf{i} } \) (que se puede demostrar con la regla de la derecha). De la ecuación \eqref{fuerzamag}, vemos que la fuerza magnética se dirige hacia la izquierda, a lo largo de la dirección negativa del eje X. Su magnitud es \(ILB \). Por lo tanto, si se aplica una fuerza de la misma magnitud pero en dirección opuesta sobre la barra, la condición expresada en la ecuación \eqref{f0} se satisface. La fuerza que debe aplicarse es entonces
\begin{equation}
\vec{F}=ILB\,\hat{\textbf{i}},
\end{equation}
que numéricamente es
\begin{equation}
\vec{F}=(0.93\,\text{A})(0.4\,\text{m})(1.4\,\text{T})\hat{\textbf{i}},
\end{equation}
\begin{equation}
\vec{F}\approx 0.52\,\text{N}\,\hat{\textbf{i}}.
\end{equation}
[/mepr-show]
You need to be registered and logged in to take this quiz. Log in



Leave A Comment