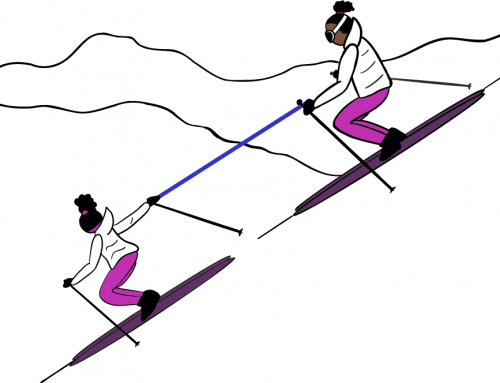
Dos bebés pandaa juegan con un juguete, como suelen hacer los bebés panda. Suponiendo que el sistema actúa como una polea ideal, ¿qué pasará si un tercer panda bebé salta y se agarra a un lado de la cuerda? Describa el movimiento de los bebés pandas según las indicaciones a continuación:
(a) Calcule la aceleración de los panda en términos de \(g\).
(b) Encuentre la tensión en la cuerda en términos de la masa de un bebé panda y \(g\).
Suponga que todos los bebés panda tienen el mismo peso.
a) Intente relacionar la aceleración neta de los pandas de la derecha con la aceleración neta del panda de la izquierda. Con esa relación en mente, dibuje dos diagramas de cuerpo libre y utilícelos para resolver el problema.
b) Con la respuesta obtenida en la parte a), la tensión se puede encontrar usando las ecuaciones para las fuerzas basadas en los diagramas de cuerpo libre.
a) La segunda ley de Newton para el panda de la izquierda implica:
\begin{equation*}
T-mg=ma_L.
\end{equation*}
Y la misma ley para los pandas de la derecha implica que
\begin{equation*}
T-2 mg = 2ma_R.
\end{equation*}
Combinando ambas ecuaciones y considerando que las aceleraciones de los pandas están relacionadas por \( a_R = – a_L \), obtenemos, después de algo de álgebra:
\begin{equation*}
a_L = \frac{g}{3}.
\end{equation*}
Entonces
\begin{equation*}
a_R = -\frac{g}{3},
\end{equation*}
porque los pandas adecuados están cayendo.
b) Reemplace una de las aceleraciones en la ecuación correspondiente de la Segunda Ley de Newton. El resultado es:
\begin{equation*}
T = \frac{4mg}{3}.
\end{equation*}
Para obtener una explicación más detallada de cualquiera de estos pasos, haga clic en “Solución detallada”.
1. Estrategia general para (a)
(a) La primera parte del problema nos pide que determinemos la aceleración de los pandas en términos de la constante gravitacional \(g\). Para abordar la pregunta, y al igual que con todos los problemas que involucran fuerzas y aceleración, comenzaremos haciendo un diagrama de cuerpo libre para los pandas. Luego usaremos la Segunda Ley de Newton para relacionar las fuerzas con la aceleración de los pandas.
2. Identificar las fuerzas y realizar un diagrama de cuerpo libre
Comencemos con el diagrama de cuerpo libre. Haremos un diagrama de cuerpo libre para el panda de la izquierda y trataremos a los dos pandas de la derecha como si fueran un solo sistema. (Al resolver un problema, siempre podemos agrupar dos o más objetos en un solo sistema si su movimiento está relacionado. Si los dos objetos no se mueven exactamente de la misma manera, entonces hacer esto puede no ser conveniente).
Sabemos que para el panda de la izquierda y para los pandas de la derecha, existe una fuerza de tensión dirigida hacia arriba en ambos casos. La magnitud de la tensión en ambos lados es la misma ya que estamos considerando que la polea en la parte superior no tiene fricción y la cuerda no se estira. La otra fuerza que podemos identificar es el peso de cada panda, que se dirige hacia abajo, y tiene magnitud \( mg \), donde \( m \) es la masa de un panda y \( g \) es la aceleración gravitacional en la tierra. Por lo tanto, el diagrama de cuerpo libre del panda de la izquierda se muestra en la Figura 1.
Figura 1: diagrama de cuerpo libre para el panda de la izquierda. Las fuerzas ejercidas sobre él son la tensión \(\vec{T}\) y el peso \(\vec{W}=-mg\,\hat{\textbf{j}}\). El sistema de coordenadas se elige con el eje Y positivo hacia arriba.
Para los otros dos pandas, podemos tratarlos como un solo sistema con un peso total \( W_T \) dado por el peso combinado de ambos pandas. Para este sistema de dos pandas, también hay tensión hacia arriba. Por tanto, el diagrama de cuerpo libre se muestra en la Figura 2.
Figura 2: diagrama de cuerpo libre para los pandas correctos. Las fuerzas ejercidas sobre ellos son la tensión \(\vec{T}\) y el peso total \(\vec{W}_T=-mg\,\hat{\textbf{j}}-mg\,\hat{\textbf{j}}\). El sistema de coordenadas se elige con el eje Y positivo hacia arriba.
Observe que la tensión en ambos lados es exactamente la misma con la misma dirección (positiva a lo largo del eje \({y-} \)) y la misma magnitud.
3. Segunda ley de Newton en la dirección \({y-} \)
Usaremos la segunda ley de Newton a lo largo del eje \({y-} \) para el panda de la izquierda, para escribir
\begin{equation}
\label{newtonl}
T\,\hat{\textbf{j}}-mg\,\hat{\textbf{j}}=ma_{L}\,\hat{\textbf{j}},
\end{equation}
donde \( a_L \) es la aceleración del panda de la izquierda. Descartando la notación vectorial porque todas las cantidades apuntan a lo largo del mismo eje, obtenemos de la ecuación \eqref{newtonl}
\begin{equation}
\label{newtonl2}
T-mg=ma_L.
\end{equation}
Podemos hacer lo mismo con los pandas de la derecha y escribir la segunda ley de Newton en la dirección \({y-} \) como
\begin{equation}
\label{newtonr}
T\,\hat{\textbf{j}}-mg\,\hat{\textbf{j}}-mg\,\hat{\textbf{j}}=(m+m)a_R\,\hat{\textbf{j}},
\end{equation}
donde en el lado derecho de la ecuación anterior, escribimos la masa total de los pandas \( m + m \) y su aceleración, denotada por \( a_R \). Al descartar la notación vectorial porque todas las cantidades están a lo largo del mismo eje, obtenemos, de la ecuación \eqref{newtonr},
\begin{equation}
\label{newtonr2}
T-2mg=2ma_R,
\end{equation}
donde hemos sumado los pesos para obtener \( -2mg \).
4. Resuelva las variables desconocidas manipulando las ecuaciones.
Hasta ahora, tenemos dos ecuaciones y tres incógnitas: la tensión \(T\), la aceleración \(a_L\) y la aceleración \(a_R\). Por lo tanto, para que podamos resolver el problema, necesitamos una ecuación adicional que incluya estas incógnitas. Esta ecuación adicional será una relación entre la aceleración del panda a la izquierda y los pandas a la derecha.
Note que los pandas cuelgan de la misma cuerda (ideal), que pasa a través de una polea simple. Es fácil, entonces, ver que si los pandas de la derecha se mueven hacia abajo, el panda de la izquierda debe ir hacia arriba y viceversa. Además, si los pandas de la derecha caen 2 metros, el panda de la izquierda subirá estos mismos 2 metros. La misma idea se aplica a la velocidad y la aceleración. Teniendo en cuenta que la aceleración es un vector, sabemos que las magnitudes de las aceleraciones \( a_R \) y \( a_L \) deben ser iguales, pero en dirección opuesta. (Nuevamente, porque si los pandas de la derecha aceleran hacia arriba, el panda de la izquierda debe acelerar hacia abajo y viceversa). Esto nos lleva a escribir la relación intuitiva pero útil
\begin{equation}
a_R\,\hat{\textbf{j}}=-a_L\,\hat{\textbf{j}}.
\end{equation}
Al descartar la notación vectorial y enfocándonos en los componentes, obtenemos
\begin{equation}
\label{ligadura}
a_R=-a_L.
\end{equation}
Ahora podemos usar la relación dada en la ecuación \eqref{ligadura} junto con las ecuaciones \eqref{newtonl2} y \eqref{newtonr2} para despejar la aceleración. Comencemos despejando \(T\) en la ecuación \eqref{newtonl2} para obtener
\begin{equation}
\label{newtonl3}
T=mg+ma_L.
\end{equation}
Al usar este resultado en la ecuación \eqref{newtonr2}, obtenemos
\begin{equation}
(mg+ma_L)-2mg=2ma_R.
\end{equation}
Ahora, en la ecuación anterior, usemos la relación de las aceleraciones dada por la ecuación \eqref{ligadura}. Explícitamente,
\begin{equation}
mg+ma_L-2mg=2m(-a_L).
\end{equation}
Podemos reorganizar nuestros términos en la ecuación anterior de modo que todos los términos, incluido \(a_L\), terminen a la izquierda y todos los términos conocidos, a la derecha. Es decir,
\begin{equation}
ma_L+2ma_L=2mg-mg,
\end{equation}
que, después de sumarlos, es
\begin{equation}
3ma_L=mg.
\end{equation}
Entonces podemos despejar \(a_L\) para finalmente obtener
\begin{equation}
a_L=\frac{mg}{3m}.
\end{equation}
Esto se simplifica aún más después de cancelar la masa:
\begin{equation}
\label{al}
a_L=\frac{g}{3}.
\end{equation}
Por lo tanto, el panda de la izquierda se mueve hacia arriba con una aceleración de magnitud \(g / 3 \). Podemos escribir esto como
\begin{equation}
\label{alvector}
\vec{a}_L=\frac{g}{3}\,\hat{\textbf{j}}.
\end{equation}
Asimismo, los pandas de la derecha se mueven con una aceleración de la misma magnitud (\( g/3 \)) pero en la dirección opuesta (usando la ecuación \eqref{ligadura} ). En particular, podemos escribir esa aceleración como
\begin{equation}
\vec{a}_R=-\frac{g}{3}\,\hat{\textbf{j}}.
\end{equation}
5. Estrategia general para (b)
(b) Para la última parte de este problema, necesitamos calcular la tensión en la cuerda. Podemos usar la ecuación \eqref{newtonl3} junto con el resultado de la aceleración \(a_L\), dado por la ecuación \eqref{al}, para obtener la tensión.
6. Manipule las ecuaciones para despejar las variables desconocidas
Si usamos la ecuación \eqref{newtonl3} junto con el resultado de la aceleración \(a_L\), dado por la ecuación \eqref{al}, obtenemos
\begin{equation}
T=mg+m\left(\frac{g}{3}\right).
\end{equation}
Después de sumar las fracciones, obtenemos
\begin{equation}
T=\frac{4mg}{3}.
\end{equation}
Recuerde que la magnitud de la tensión es la misma a lo largo de la cuerda.
You need to be registered and logged in to take this quiz. Log in




Leave A Comment