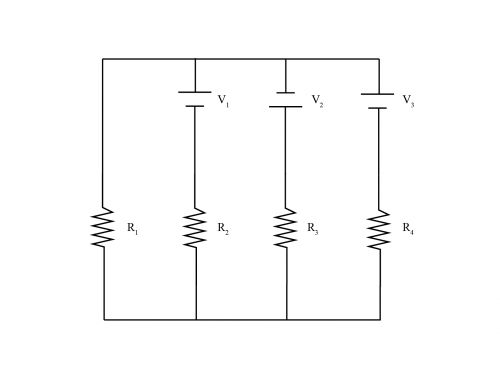
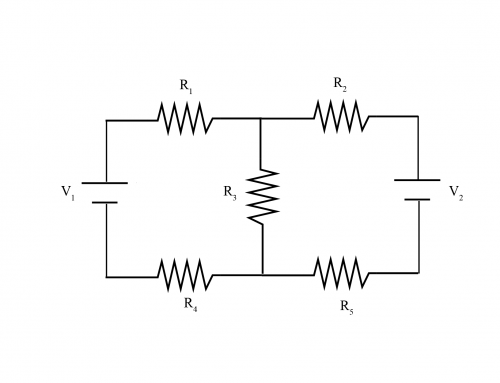
Para el circuito que se muestra en la figura, encuentre la resistencia equivalente.
Para obtener una explicación más detallada de cualquiera de estos pasos, haga clic en “Solución detallada”. [/mepr-show] Para encontrar la resistencia equivalente del circuito, necesitamos identificar grupos de resistencias que están en serie (que tendrán la misma corriente) o en paralelo (que tendrán el mismo voltaje). Después de reducir estas resistencias a su resistencia equivalente, repetimos este procedimiento en todo el circuito hasta que lo reduzcamos a una sola resistencia conectada a la emf fuente. [mepr-show rules=”4409″ unauth=”both”] La siguiente figura muestra el circuito con etiquetas únicas para sus resistencias. Será útil identificar resistencias individuales a lo largo de la solución. Observe en esta figura que las resistencias \ (R_1 \) y \ (R_2 \) están conectadas a lo largo del mismo cable, y el cable entre ellas no se ramifica. Por lo tanto, \ (R_1 \) y \ (R_2 \) tendrán la misma corriente y, por lo tanto, estarán conectados en serie. Lo mismo ocurre con los pares de resistencias \ (R_5 \) y \ (R_6 \), \ (R_8 \) y \ (R_9 \), y \ (R_{10} \) y \ (R_{11} \) respectivamente. La resistencia equivalente para resistencias conectadas en serie está dada por la suma de las resistencias de cada resistor. Dado que todas las resistencias tienen resistencia \ (R \), la resistencia equivalente para los cuatro pares de resistencias es simplemente \ (R + R = 2R \). Sea \ (R’_1 \) la resistencia equivalente para \ (R_1 \) y \ (R_2 \), \ (R’_2 \) denota la resistencia equivalente para \ (R_5 \) y \ (R_6 \), \ (R’_3 \) denota la resistencia equivalente para \ (R_8 \) y \ (R_9 \), y \ (R’_4 \) denota la resistencia equivalente para \ (R_{10} \) y \ (R_{11} \). Por lo tanto, como se explicó anteriormente, sus resistencias son \begin{equation} Después de sustituir estas resistencias equivalentes, el circuito se convierte en el siguiente: Ahora, observe que \ (R_3 \) y \ (R’_2 \) tienen la misma conexión de cables en cada terminal de las resistencias. Lo mismo ocurre con las resistencias \ (R_7 \) y \ (R’_3 \) como se muestra en la siguiente figura, donde se dibujan diferentes segmentos continuos de alambre con diferentes patrones: Los cables contiguos (los dibujados con los mismos patrones) tienen el mismo voltaje y, por lo tanto, están conectados en paralelo. La resistencia equivalente \ (R’_5 \) para las resistencias \ (R_3 \) y \ (R’_2 \) viene dada por: \begin{equation} que podemos escribir de forma equivalente como \begin{equation} Al invertir las fracciones en ambos lados, esto se convierte en: \begin{equation} Finalmente, después de sustituir \ (R_3 = R \) y \ (R’_2 = 2R \) en la ecuación. \ eqref{EQ:1} , obtenemos: \begin{equation} De manera análoga, para \ (R_7 \) y \ (R’_3 \) la resistencia equivalente \ (R’_6 \) está dada por: \begin{equation} Observe que desde \ (R_7 = R_3 = R \), \ (R’_3 = R’_2 = 2R, \) y esta ecuación tiene exactamente la misma forma que la ecuación \ eqref{EQ:2} , entonces esta ecuación producirá exactamente el mismo resultado que \ (R’_5 \) (pero ahora necesitamos resolver para \ (R’_6 \)). Por tanto, tenemos: \begin{equation} Después de reemplazar \ (R_3 \) y \ (R’_2 \) por su resistencia equivalente \ (R’_5 \), y \ (R_7 \) y \ (R’_3 \) por su resistencia equivalente \ (R’_6 \), el circuito se vuelve como se muestra en la siguiente figura: Ahora, las resistencias \ (R’_1 \) y \ (R’_5 \) están en serie porque, como se mencionó en el primer paso para las resistencias \ (R_1 \) y \ (R_2 \), están conectadas a lo largo del mismo cable y el cable entre ellos no se ramifica. Por tanto, su resistencia equivalente \ (R’_7 \) está dada por \begin{equation} De la ecuación \ eqref{EQ:1} , tenemos \ (R’_1 = 2R, \) y de la ecuación \ eqref{EQ:2} , tenemos \ (R’_5 = \ frac{2}{3} R. \) Por lo tanto, después de sustituir estos valores en la ecuación anterior, obtenemos: \begin{equation} De manera análoga, las resistencias \ (R’_4 \) y \ (R’_6 \) están en serie. Por tanto, su resistencia equivalente \ (R’_8 \) viene dada por: \begin{equation} De la ecuación \ eqref{EQ:1} , vemos que \ (R’_4 = 2R \), y de la ecuación \ eqref{EQ:2} encontramos que \ (R’_6 = \ frac{2}{3} R \). Por lo tanto \begin{equation} y el circuito resultante después de sustituir los dos pares de resistencias por sus resistencias equivalentes se muestra en la siguiente figura: Finalmente, como podemos ver en esta figura, las tres resistencias \ (R_4, R’_7, \) y \ (R’_8 \) están en paralelo. Por tanto, su resistencia equivalente \ (R’_9 \) está dada por \begin{equation} Si invertimos las fracciones en cada lado de la ecuación, obtenemos: \begin{equation} De las ecuaciones \ eqref{EQ:3} y \ eqref{EQ:4} , sabemos que \ (R’_7 = R’_8 = \ frac{8}{3} R \). También sabemos por la segunda figura que \ (R_4 = R \). Por lo tanto, \begin{equation} Si reemplazamos las resistencias \ (R_4, R’_7, \) y \ (R’_8 \) por la resistencia equivalente \ (R’_9 \), obtenemos el circuito que se muestra en la siguiente figura: Como hemos reducido el circuito a una sola resistencia conectada a la fuente de poder, \ (R’_9 \) es la resistencia equivalente del circuito. Por eso, \begin{equation} [/mepr-show] You need to be registered and logged in to take this quiz. Log in
\label{EQ:1}
R’_1 = R’_2 = R’_3 = R’_4 = 2R.
\end{equation}
\ frac{1} {R’_5} = \ frac{1}{R_3} + \ frac{1} {R’_2},
\end{equation}
\label{EQ:2}
\ frac{1} {R’_5} = \ frac {\ frac{1}{R_3} + \ frac{1} {R’_2}}{1} .
\end{equation}
R’_5 = \ frac{1} {\ frac{1}{R_3} + \ frac{1} {R’_2}}.
\end{equation}
R’_5 = \ frac{1} {\ frac{1}{R}+\frac{1}{2R}}
= \ frac{1} {\ frac{1} {R (1 + \ frac{1}{2})}}
= \frac{2}{3}R.
\end{equation}
\ frac{1} {R’_6} = \ frac{1}{R_7} + \ frac{1} {R’_3}.
\end{equation}
R’_6 = R’_5 = \ frac{2}{3} R.
\end{equation}
R’_7 = R’_1 + R’_5.
\end{equation}
\label{EQ:3}
R’_7 = \ frac{2}{3} R + 2 R = \ frac{8}{3} R.
\end{equation}
R’_8 = R’_4 + R’_6.
\end{equation}
\label{EQ:4}
R’_8 = 2R + \ frac{2}{3} R = \ frac{8}{3} R,
\end{equation}
\ frac{1} {R’_9} = \ frac{1}{R_4} + \ frac{1} {R’_7} + \ frac{1} {R’_8}.
\end{equation}
R’_9 = \ frac{1} {\ frac{1}{R_4} + \ frac{1} {R’_7} + \ frac{1} {R’_8}}.
\end{equation}
R’_9 = \ frac{1} {\ frac{1}{R} + \ frac{1} {\ frac{8}{3} R} + \ frac{1} {\ frac{8}{3} R}}
= \ frac{1} {\ frac{1}{R} + \frac{3}{8R} + \frac{3}{8R} }
= \ frac{1} {\ frac{8}{8R} + \frac{3}{8R} + \frac{3}{8R}}
= \ frac{1} {\ frac {8 + 3 + 3}{8R} }
= \ frac{1} {\ frac{14}{8R} } = \ frac{1} {\ frac{7}{4R}}
= \frac{4}{7} R.
\end{equation}
R_{eq} = R’_9 = \ frac{4}{7} R.
\end{equation}




Leave A Comment