¡Tanque lleno de agua!

Use la ecuación de Bernoulli y la ecuación de continuidad para obtener una relación entre \(H\) y \(v_B\). Luego, use ecuaciones cinemáticas para obtener el tiempo y la relación entre \(v_B\) y \(H_0\), para finalmente relacionar \(H\) con \(H_0\).

La ecuación de Bernoulli dice:

\begin{equation*}
P_A + \rho g h_A + \frac{1}{2} \rho v_A^2 = P_B + \rho g h_B + \frac{1}{2} \rho v_B^2,
\end{equation*}

[mepr-show rules=”4409″ unauth=”both”]

donde aplicando las condiciones dadas tenemos:

\begin{equation*}
gH + \frac{1}{2} v_A^2 = \frac{1}{2} v_B^2.
\end{equation*}

Por la ecuación de continuidad \(A_A v_A = A_B v_B\), la velocidad \(v_A\) es proporcional a \(A_B / A_A\). El resultado es aproximadamente:

\begin{equation*}
v_A \approx 0.
\end{equation*}

Entonces, despejando \(H\) tenemos:

\begin{equation*}
H = \frac{v_B^2}{2g}.
\end{equation*}

El desplazamiento \(L\) se puede escribir como:

\begin{equation*}
v_B = \frac{L}{t_f}.
\end{equation*}

Por la ecuación cinemática para la posición tenemos:

\begin{equation*}
\vec{y} = \vec{y}_i + \vec{v}_{y,i} t + \frac{1}{2} \vec{a} t^2,
\end{equation*}

donde con las condiciones dadas tenemos:

\begin{equation*}
t_f^2 = \frac{2H_0}{g}.
\end{equation*}

Combinando las relaciones anteriores y despejando \(H\) en función de \(H_0\) obtenemos:

\begin{equation*}
H = \frac{L^2}{4 H_0},
\end{equation*}

que con valores numéricos es:

\begin{equation}
H = 1 \, \text{m}.
\end{equation}

Para obtener una explicación más detallada de cualquiera de estos pasos, haga clic en “Solución detallada”.

[/mepr-show]

Para encontrar la altura de la columna de agua, podemos usar la ecuación de Bernoulli para relacionar esta altura con la velocidad del agua una vez que sale del tanque. Luego, podemos usar ecuaciones cinemáticas para encontrar esta velocidad en términos de las distancias verticales y horizontales recorridas por el agua cuando cae hacia el suelo.

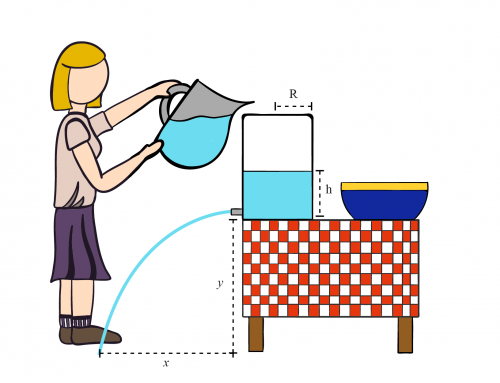
Consideremos los puntos A y B, como se muestra en la figura 1.

El punto A está en la superficie del tanque y el punto B está justo afuera de la pequeña abertura. La ecuación de Bernoulli para estos dos puntos viene dada por

\begin{equation}
\label{EQ:B}
P_A + \rho g h_A + \frac{1}{2} \rho v_A^2 = P_B + \rho g h_B + \frac{1}{2} \rho v_B^2,
\end{equation}

[mepr-show rules=”4409″ unauth=”both”]

donde \(P_A\) es la presión en el punto \(A\), \(\rho\) es la densidad del fluido, \(h_A\) es la altura del punto \(A\) en relación con el marco de referencia que se muestra en la siguiente figura, y \(v_A\) es la rapidez del fluido en el punto \(A\). Los nombres de las variables son análogos para el punto \(B\). Reescribamos estas variables en términos de las conocidas.

Primero, observe que los puntos \(A\) y \(B\) están directamente expuestos a la atmósfera y no hay líquido sobre ellos. Por lo tanto, la presión en estos puntos es la presión atmosférica, es decir

\begin{equation}
P_A = P_B = P_{\text{atm}}.
\end{equation}

Sustituyendo esto en la ecuación. \eqref{EQ:B} obtenemos

\begin{equation}
P_{\text{atm}} + \rho g h_A + \frac{1}{2} \rho v_A^2 = P_{\text{atm}} + \rho g h_B + \frac{1}{2} \rho v_B^2,
\end{equation}

y después de restar \(P_{\text{atm}}\) en ambos lados, obtenemos

\begin{equation}
\rho g h_A + \frac{1}{2} \rho v_A^2 = \rho g h_B + \frac{1}{2} \rho v_B^2.
\end{equation}

Ahora podemos dividir por \(\rho\) en ambos lados. Esto produce

\begin{equation}
\label{EQ:B2}
g h_A + \frac{1}{2} v_A^2 = g h_B + \frac{1}{2} v_B^2.
\end{equation}

En segundo lugar, en la figura 2, podemos notar que \(h_A = H_0 + H\) y \(h_B = H_0\). Si sustituimos esto en la ecuación. \eqref{EQ:B2} , obtenemos

\begin{equation}
g (H_0 + H) + \frac{1}{2} v_A^2 = g H_0 + \frac{1}{2} v_B^2,
\end{equation}

o, de manera equivalente

\begin{equation}
g H_0 + gH + \frac{1}{2} v_A^2 = g H_0 + \frac{1}{2} v_B^2.
\end{equation}

Si restamos \(gH_0\) de ambos lados de la ecuación, obtenemos

\begin{equation}
\label{EQ:VB3}
gH + \frac{1}{2} v_A^2 = \frac{1}{2} v_B^2.
\end{equation}

En tercer lugar, podemos relacionar \(v_A\) y \(v_B\) usando la ecuación de continuidad. El caudal volumétrico \(I\) de un fluido en un punto \(P\) en un líquido que fluye a través de un tubo viene dado por

\begin{equation}
\label{EQ:I}
I_{V,P} = A_P v_P,
\end{equation}

donde \(A_P\) es el área de la sección transversal del recipiente y \(v_P\) es la rapidez del fluido en el punto \(P\). Suponiendo que el movimiento del fluido es constante en todos los puntos, el caudal volumétrico es constante. Por lo tanto, para los puntos A y B, tenemos

\begin{equation}
I_{V,A} = I_{V,B}.
\end{equation}

De la ecuación \eqref{EQ:I} , podemos reescribir esta ecuación como

\begin{equation}
\label{EQ:C}
A_A v_A = A_B v_B,
\end{equation}

donde \(A_A\) es el área de la sección transversal del tubo en el punto \(A\), \(v_A\) es la rapidez del fluido en el punto \(A\) y de manera análoga para \(A_B\) y \(v_B\) en el punto \(B\). Resolviendo esta ecuación. para \(v_A\) obtenemos

\begin{equation}
v_A = \frac{A_B}{A_A v_B}.
\end{equation}

Ahora, dado que el área de la sección transversal del tanque \(A_A\) es mucho mayor que el área de la sección transversal de la abertura \(A_B\). La fracción \(\frac{A_B}{A_A}\) será un número muy pequeño. Por tanto, podemos hacer la aproximación de que la rapidez con la que se mueve el agua en el punto \(A\) es cero, es decir

\begin{equation}
v_A = 0,
\end{equation}

y sustituyendo esto en la ecuación. \eqref{EQ:VB3} obtenemos

\begin{equation}
gH + \frac{1}{2} 0^2 = \frac{1}{2} v_B^2.
\end{equation}

Esto se puede reescribir como

\begin{equation}
gH = \frac{1}{2} v_B^2,
\end{equation}

y dividir por \(g\) en ambos lados obtenemos
\begin{equation}
\label{EQ:H}
H = \frac{v_B^2}{2g}.
\end{equation}

Tenemos una ecuación para H; sin embargo, todavía necesitamos escribir \(v_B\) en términos de otras variables conocidas. Consideremos el movimiento de una molécula de agua cuando sale del pequeño agujero en el punto \(B\). La única fuerza que actúa sobre esta molécula es su peso, que actúa en dirección vertical. Por tanto, la molécula seguirá un movimiento con aceleración constante en la dirección vertical y un movimiento con velocidad constante en la dirección horizontal. Definamos un marco de referencia, como se muestra en la segunda figura. Según él, la ecuación que describe el movimiento en la dirección \(x\) es

\begin{equation}
\label{EQ:X}
\vec{x}(t) = \vec{x}_i + \vec{v}_{x,i} t,
\end{equation}

donde \(\vec{x}(t)\) es la posición \(x\) de la molécula en el tiempo \(t\), \(\vec{x}_i\) es su posición \(x\) en \(t=0\), y \(\vec{v}_{x,i}\) es la componente \(x\) de su velocidad en \(t = 0\) (que permanecerá igual para \(t>0\)).

Sea \(t=0\) el momento en que la molécula de agua sale del agujero en el punto \(B\). De acuerdo con esto, tenemos que \(v_{x,i} = v_B\), y así, de acuerdo con el marco de referencia que se muestra en la segunda figura, podemos escribir \(\vec{v}_{x,i} = v_B\hat{i}\). Si sustituimos esto en la ecuación. \eqref{EQ:X} , obtenemos

\begin{equation}
\label{EQ:X1}
\vec{x}(t) = \vec{x}_i + v_B t \hat{i}.
\end{equation}

Además, de acuerdo con nuestro marco de referencia tenemos \(\vec{x}_i = \vec{0}\), y podemos escribir \(\vec{x}(t) = x(t) \hat{i}\). Con esto, la ecuación \eqref{EQ:X1} se convierte en

\begin{equation}
x(t) \hat{i} = v_B t \hat{i},
\end{equation}

y si consideramos solo las magnitudes, obtenemos

\begin{equation}
\label{EQ:X2}
x(t) = v_B t.
\end{equation}

Esta ecuación es válida para todos los tiempos \(t\) durante el intervalo en el que la molécula de agua cae desde el punto \(B\) hacia el suelo. En particular, es válido justo antes de tocar el suelo. Sea \(t_f\) el momento en el que esto ocurre. Según nuestro marco de referencia, la posición en este momento será

\begin{equation}
x(t = t_f) = L.
\end{equation}

Sustituyendo esto en la ecuación. \eqref{EQ:X2} se cumple que

\begin{equation}
\label{EQ:X3}
L = v_B t_f,
\end{equation}

y despejando \(v_B\) obtenemos

\begin{equation}
\label{EQ:VB22}
v_B = \frac{L}{t_f}
\end{equation}

Hemos encontrado una expresión para \(v_b\) que incluye la variable conocida L y la variable desconocida \(t_f\). Ahora necesitamos escribir \(t_f\) en términos de variables conocidas. Para hacerlo, podemos usar la ecuación de movimiento en la dirección \(y\), que viene dada por

\begin{equation}
\label{EQ:Y}
\vec{y}(t) = \vec{y}_i + \vec{v}_{y,i} t + \frac{1}{2} \vec{a} t^2,
\end{equation}

donde \(\vec{y}(t)\) es la posición \(y\) de la molécula en el tiempo \(t\), \(\vec{y}_i\) es su posición \(y\) en \(t=0, \vec{v}_{y,i}\) es la componente \(y\) de su velocidad en \(t = 0\), y \(\vec{a}\) es su aceleración.

En el momento en que la molécula de agua sale del agujero en el punto \(B\), está experimentando un movimiento horizontal. Por lo tanto \(\vec{y}_i = \vec{0}\). Con esto, la ecuación \eqref{EQ:Y} se convierte en

\begin{equation}
\label{EQ:Y2}
\vec{y}(t) = \vec{y}_i + \frac{1}{2} \vec{a} t^2.
\end{equation}

Ahora, de la segunda figura, notamos que en nuestro marco de referencia tenemos que \(y_i = H_0\), y por lo tanto \(\vec{y}_i = H_0 \hat{j}\). Además, en este caso \(\vec{a} = -g\hat{j}\), y podemos escribir \(\vec{y}(t) = y(t) \hat{j}\). Sustituyendo todo esto en la ecuación. \eqref{EQ:Y2} obtenemos

\begin{equation}
y(t) \hat{j} = H_0 \hat{j} -\frac{1}{2} g t^2 \hat{j},
\end{equation}

y si consideramos solo las magnitudes, obtenemos

\begin{equation}
\label{EQ:Y3}
y(t) = H_0 – \frac{1}{2} g t^2.
\end{equation}

Además, según nuestro marco de referencia (ver la segunda figura), una molécula de agua golpeará el suelo en un momento \(t = t_f\) tal que \(y(t_f) = 0\). En este momento, la ecuación. \eqref{EQ:Y3} se convierte en

\begin{equation}
0 = H_0 – \frac{1}{2}gt_f^2,
\end{equation}

que podemos reescribir como

\begin{equation}
\label{EQ:Y4}
\frac{1}{2} gt_f^2 = H_0.
\end{equation}

Resolviendo para \(t_f^2\) obtenemos

\begin{equation}
\label{EQ:TF}
t_f^2 = \frac{2H_0}{g}.
\end{equation}

Esta ecuación y la ecuación. \eqref{EQ:VB} se pueden utilizar para obtener una expresión para \(v_B\) en términos de variables conocidas. Si elevamos la ecuación al cuadrado. \eqref{EQ:VB22} en ambos lados, obtenemos

\begin{equation}
v_B^2 = \frac{L^2}{ t_f^2},
\end{equation}

y sustituyendo la ecuación \eqref{EQ:TF} obtenemos

\begin{equation}
v_B^2 = \frac{L^2}{ \frac{2H_0}{g} }
= \frac{L^2 g }{ 2H_0}.
\end{equation}

Finalmente, después de sustituir esto en la ecuación. \eqref{EQ:H} , encontramos que la altura de la columna de agua en el tanque es

\begin{equation}
H = \frac{1}{2g} \frac{L^2 g }{2H_0}
= \frac{L^2}{4 H_0},
\end{equation}

e insertando valores numéricos da

\begin{equation}
H = \frac{(2 \ \text{m})^2}{4 \ \text{m}} = 1 \ \text{m}.
\end{equation}

[/mepr-show]

You need to be registered and logged in to take this quiz. Log in