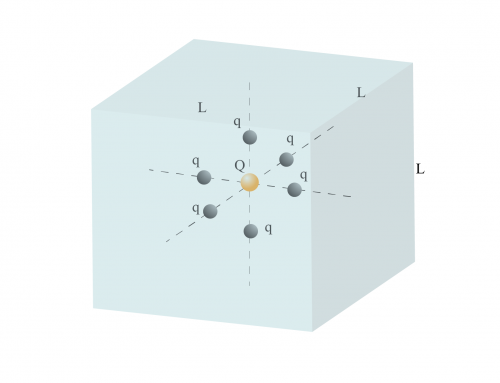
Un cubo con una longitud de lado de 25 cm tiene 8 cargas de \(6 \, \mu \text{C} \), cada una ubicada en cada esquina. Calcule el campo eléctrico total generado en el medio de cada una de las caras del cubo.
Escriba un vector que se origine en una partícula y termine en el medio de cualquier cara del cubo. Luego, use el principio de superposición para campos eléctricos.
Para una carga puntual, el campo eléctrico es:
\begin{equation*}
\vec{E}=\frac{1}{4\pi\epsilon_0}\frac{q}{r^2}\,\hat{\textbf{r}},
\end{equation*}
[mepr-show rules=”4409″ unauth=”both”]
donde \(\hat{\textbf{r}}=\frac{\vec{r}}{r} \). Para la mitad de cualquier cara del cubo, la posición de los vectores para cada partícula es:
\begin{equation}
\vec{r}_i = \vec{a}_P – \vec{a}_i,
\end{equation}
donde \(\vec{a} _P \) es el vector del sistema de coordenadas y \(a_i \) el vector desde sistema de coordenadas a la partícula \(i \).
Para la partícula 1:
\begin{equation*}
\vec{r}_1=-\frac{s}{2}\,\hat{\textbf{i}}+s\,\hat{\textbf{j}}-\frac{s}{2}\,\hat{\textbf{k}}.
\end{equation*}
Para la partícula 2:
\begin{equation*}
\vec{r}_2=\frac{s}{2}\,\hat{\textbf{i}}+s\,\hat{\textbf{j}}-\frac{s}{2}\,\hat{\textbf{k}}.
\end{equation*}
Para la partícula 3:
\begin{equation*}
\vec{r}_3=\frac{s}{2}\,\hat{\textbf{i}}-\frac{s}{2}\,\hat{\textbf{k}}.
\end{equation*}
Para la partícula 4:
\begin{equation*}
\vec{r}_4=-\frac{s}{2}\,\hat{\textbf{i}}-\frac{s}{2}\,\hat{\textbf{k}}.
\end{equation*}
Para la partícula 5:
\begin{equation*}
\vec{r}_5=-\frac{s}{2}\,\hat{\textbf{i}}+s\,\hat{\textbf{j}}+\frac{s}{2}\,\hat{\textbf{k}}.
\end{equation*}
Para la partícula 6:
\begin{equation*}
\vec{r}_6=\frac{s}{2}\,\hat{\textbf{i}}+s\,\hat{\textbf{j}}+\frac{s}{2}\,\hat{\textbf{k}}.
\end{equation*}
Para la partícula 7:
\begin{equation*}
\vec{r}_7=\frac{s}{2}\,\hat{\textbf{i}}+\frac{s}{2}\,\hat{\textbf{k}}.
\end{equation*}
Para la partícula 8:
\begin{equation*}
\vec{r}_8=-\frac{s}{2}\,\hat{\textbf{i}}+\frac{s}{2}\,\hat{\textbf{k}}.
\end{equation*}
La superposición del campo eléctrico es:
\begin{equation*}
\vec{E}=\frac{q}{4\pi\epsilon_0}\sum_{i=1}^{8}\frac{\vec{r}_i}{r_i^3},
\end{equation*}
la cual es:
\begin{equation*}
\vec{E}=\frac{q}{4\pi\epsilon_0}\frac{4}{s^2\left(\frac{3}{2}\right)^{3/2}}\,\hat{\textbf{j}},
\end{equation*}
que con valores numéricos es:
\begin{equation*}
\vec{E}\approx 1.88\times 10^{6}\,\text{N/C}\,\hat{\textbf{j}}.
\end{equation*}
Para obtener una explicación más detallada de cualquiera de estos pasos, haga clic en “Solución detallada”.
[/mepr-show]
Necesitamos encontrar el campo eléctrico total generado en el medio de cada una de las caras del cubo. Para resolver este problema, debemos encontrar el campo eléctrico producido por cada carga puntual en el punto especificado en la matriz de cubos (el medio de una de sus facetas) y luego hacer la suma vectorial. El punto en el que se calcula el campo eléctrico se denotará como P. El campo eléctrico \(\vec{E} \) producido por una carga puntual \(q \) está dado por
\begin{equation}
\label{efield}
\vec{E}=\frac{1}{4\pi\epsilon_0}\frac{q}{r^2}\,\hat{\textbf{r}},
\end{equation}
[mepr-show rules=”4409″ unauth=”both”]
donde \(\vec{r} \) es el vector desde la carga puntual hasta donde se calcula el campo eléctrico. La magnitud de este vector es \(r \), y el vector unitario \(\hat {\textbf{r} }\) Se define como
\begin{equation}
\label{rhat}
\hat{\textbf{r}}=\frac{\vec{r}}{r}.
\end{equation}
Usando la expresión para \(\hat {\textbf{r} } \) dada en la ecuación \eqref{rhat} en la ecuación \eqref{efield}, obtenemos
\begin{equation}
\vec{E}=\frac{1}{4\pi\epsilon_0}\frac{q}{r^3}\,\vec{r}.
\end{equation}
Como conocemos las coordenadas de todas las cargas puntuales y el punto P, solo tenemos que calcular el vector \(\vec{r} \) y su magnitud para cada carga. Tenga en cuenta que debido a la simetría, el campo eléctrico sería el mismo en el medio de todas las caras del cubo. Elijamos la segunda cara en el plano XZ, como se ve en la figura 1.
Figura 1: Ocho partículas cargadas colocadas en los vértices de un cubo. Colocamos el origen de nuestro sistema de coordenadas en la carga 6. También se muestra el punto P donde se debe calcular el campo eléctrico.
Etiquetamos las cargas usando números, como se muestra en la figura 2, y usamos la misma etiqueta para las coordenadas de cada una y el vector asociado \(\vec{r} \).
Figura 2: vectores unitarios a lo largo de los ejes X, Y y Z multiplicados por \(s \), la longitud de la arista del cubo. Para encontrar la posición de cada partícula, partimos del origen y sumamos los vectores hasta llegar a la carga deseada. Por ejemplo, para la carga 1 sumamos los vectores marrón y cian. De manera equivalente, también podríamos sumar los vectores amarillo y violeta para obtener la posición de la carga 1.
Usando la figura 2 como guía, las coordenadas \(\vec{a} \) de cada carga se puede dar por combinaciones lineales (diferentes sumas) de vectores unitarios; a saber,
\begin{equation}
\label{a1}
\vec{a}_1=s\,\hat{\textbf{i}}+s\,\hat{\textbf{k}},
\end{equation}
\begin{equation}
\vec{a}_2=s\,\hat{\textbf{k}},
\end{equation}
\begin{equation}
\vec{a}_3=s\,\hat{\textbf{j}}+s\,\hat{\textbf{k}},
\end{equation}
\begin{equation}
\vec{a}_4=s\,\hat{\textbf{i}}+s\,\hat{\textbf{j}}+s\,\hat{\textbf{k}},
\end{equation}
\begin{equation}
\vec{a}_5=s\,\hat{\textbf{i}},
\end{equation}
\begin{equation}
\vec{a}_6=\vec{0},
\end{equation}
\begin{equation}
\vec{a}_7=s\,\hat{\textbf{j}},
\end{equation}
\begin{equation}
\label{a8}
\vec{a}_8=s\,\hat{\textbf{i}}+s\,\hat{\textbf{j}}.
\end{equation}
Las coordenadas del punto P están dadas por
\begin{equation}
\label{ap}
\vec{a}_P=\frac{s}{2}\,\hat{\textbf{i}}+s\,\hat{\textbf{j}}+\frac{s}{2}\,\hat{\textbf{k}},
\end{equation}
como podemos ver en la figura 3:
Figura 3: Coordenadas del punto P en términos de los vectores unitarios a lo largo de los ejes X, Y y Z.
Los vectores \(\vec{r}_i \) se calculan de la siguiente manera
\begin{equation}
\vec{r}_i=\vec{a}_P-\vec{a}_i,
\end{equation}
donde \(i=\{1,2,3,4,5,6,7,8\}\). Para ilustrar esto, considere las siguientes tres figuras (figura 4, 5 y 6, respectivamente) para \(\vec{r} _1 \), \(\vec{r}_2 \) y \(\vec{r}_7 \), respectivamente.
Figura 4: La diferencia entre \(\vec{a} _P \) (el vector de posición del punto P) y el vector de posición para la carga 1 \(\vec{a}_1 \) da el vector de distancia entre el punto P y la carga 1, \(\vec{r}_1 \). En otras palabras, \(\vec{r}_1=\vec{a}_P-\vec{a}_1\).
Figura 5: La diferencia entre \(\vec{a} _P \) (el vector de posición del punto P) y el vector de posición para la carga 7 \(\vec{a} _7 \) da el vector de distancia entre el punto P y la carga 7, \(\vec{r} _7 \). En otras palabras, \(\vec{r}_7=\vec{a}_P-\vec{a}_7\).
Figura 6: La diferencia entre \(\vec{a} _P \) (el vector de posición del punto P) y el vector de posición para la carga 2 \(\vec{a} _2 \) da el vector de distancia entre el punto P y la carga 2, \(\vec{r} _2 \). En otras palabras, \(\vec{r}_2=\vec{a}_P-\vec{a}_2\).
Por lo tanto, usando las ecuaciones \eqref{a1} – \eqref{a8} y la ecuación \eqref{ap}, podemos escribir explícitamente
\begin{equation}
\vec{r}_1=\frac{s}{2}\,\hat{\textbf{i}}+s\,\hat{\textbf{j}}+\frac{s}{2}\,\hat{\textbf{k}}-(s\,\hat{\textbf{i}}+s\,\hat{\textbf{k}}),
\end{equation}
\begin{equation}
\vec{r}_1=-\frac{s}{2}\,\hat{\textbf{i}}+s\,\hat{\textbf{j}}-\frac{s}{2}\,\hat{\textbf{k}},
\end{equation}
y su magnitud
\begin{equation}
r_1=\sqrt{\left(-\frac{s}{2}\right)^2+s^2+\left(-\frac{s}{2}\right)^2},
\end{equation}
\begin{equation}
\label{r1}
r_1=s\sqrt{\frac{3}{2}}
\end{equation}
Para el vector \(\vec{r}_2 \):
\begin{equation}
\vec{r}_2=\frac{s}{2}\,\hat{\textbf{i}}+s\,\hat{\textbf{j}}+\frac{s}{2}\,\hat{\textbf{k}}-(s\,\hat{\textbf{k}}),
\end{equation}
\begin{equation}
\vec{r}_2=\frac{s}{2}\,\hat{\textbf{i}}+s\,\hat{\textbf{j}}-\frac{s}{2}\,\hat{\textbf{k}},
\end{equation}
y su magnitud
\begin{equation}
r_2=\sqrt{\left(\frac{s}{2}\right)^2+s^2+\left(\frac{s}{2}\right)^2},
\end{equation}
\begin{equation}
r_2=s\sqrt{\frac{3}{2}}
\end{equation}
Para el vector \(\vec{r}_3 \):
\begin{equation}
\vec{r}_3=\frac{s}{2}\,\hat{\textbf{i}}+s\,\hat{\textbf{j}}+\frac{s}{2}\,\hat{\textbf{k}}-(s\,\hat{\textbf{j}}+s\,\hat{\textbf{k}}),
\end{equation}
\begin{equation}
\vec{r}_3=\frac{s}{2}\,\hat{\textbf{i}}-\frac{s}{2}\,\hat{\textbf{k}},
\end{equation}
y su magnitud
\begin{equation}
r_3=\sqrt{\left(\frac{s}{2}\right)^2+\left(\frac{s}{2}\right)^2},
\end{equation}
\begin{equation}
r_3=\frac{s}{\sqrt{2}}.
\end{equation}
Para el vector \(\vec{r}_4 \):
\begin{equation}
\vec{r}_4=\frac{s}{2}\,\hat{\textbf{i}}+s\,\hat{\textbf{j}}+\frac{s}{2}\,\hat{\textbf{k}}-(s\,\hat{\textbf{i}}+s\,\hat{\textbf{j}}+\hat{\textbf{k}}),
\end{equation}
\begin{equation}
\vec{r}_4=-\frac{s}{2}\,\hat{\textbf{i}}-\frac{s}{2}\,\hat{\textbf{k}},
\end{equation}
y su magnitud
\begin{equation}
r_4=\sqrt{\left(-\frac{s}{2}\right)^2+\left(-\frac{s}{2}\right)^2},
\end{equation}
\begin{equation}
r_4=\frac{s}{\sqrt{2}}.
\end{equation}
Para el vector \(\vec{r}_5 \):
\begin{equation}
\vec{r}_5=\frac{s}{2}\,\hat{\textbf{i}}+s\,\hat{\textbf{j}}+\frac{s}{2}\,\hat{\textbf{k}}-(s\,\hat{\textbf{i}}),
\end{equation}
\begin{equation}
\vec{r}_5=-\frac{s}{2}\,\hat{\textbf{i}}+s\,\hat{\textbf{j}}+\frac{s}{2}\,\hat{\textbf{k}},
\end{equation}
y su magnitud
\begin{equation}
r_5=\sqrt{\left(-\frac{s}{2}\right)^2+s^2+\left(\frac{s}{2}\right)^2},
\end{equation}
\begin{equation}
r_5=s\sqrt{\frac{3}{2}}.
\end{equation}
Para el vector \(\vec{r}_6 \):
\begin{equation}
\vec{r}_6=\frac{s}{2}\,\hat{\textbf{i}}+s\,\hat{\textbf{j}}+\frac{s}{2}\,\hat{\textbf{k}}-(\vec{0}),
\end{equation}
\begin{equation}
\vec{r}_6=\frac{s}{2}\,\hat{\textbf{i}}+s\,\hat{\textbf{j}}+\frac{s}{2}\,\hat{\textbf{k}},
\end{equation}
y su magnitud
\begin{equation}
r_6=\sqrt{\left(\frac{s}{2}\right)^2+s^2+\left(\frac{s}{2}\right)^2},
\end{equation}
\begin{equation}
r_6=s\sqrt{\frac{3}{2}}.
\end{equation}
Para el vector \(\vec{r}_7 \):
\begin{equation}
\vec{r}_7=\frac{s}{2}\,\hat{\textbf{i}}+s\,\hat{\textbf{j}}+\frac{s}{2}\,\hat{\textbf{k}}-(s\,\hat{\textbf{j}}),
\end{equation}
\begin{equation}
\vec{r}_7=\frac{s}{2}\,\hat{\textbf{i}}+\frac{s}{2}\,\hat{\textbf{k}},
\end{equation}
y su magnitud
\begin{equation}
r_7=\sqrt{\left(\frac{s}{2}\right)^2+\left(\frac{s}{2}\right)^2},
\end{equation}
\begin{equation}
r_7=\frac{s}{\sqrt{2}}.
\end{equation}
Y, finalmente, para el vector \(\vec{r}_8 \) tenemos
\begin{equation}
\vec{r}_8=\frac{s}{2}\,\hat{\textbf{i}}+s\,\hat{\textbf{j}}+\frac{s}{2}\,\hat{\textbf{k}}-(s\,\hat{\textbf{i}}+s\,\hat{\textbf{j}}),
\end{equation}
\begin{equation}
\vec{r}_8=-\frac{s}{2}\,\hat{\textbf{i}}+\frac{s}{2}\,\hat{\textbf{k}},
\end{equation}
y su magnitud
\begin{equation}
r_8=\sqrt{\left(\frac{s}{2}\right)^2+\left(\frac{s}{2}\right)^2},
\end{equation}
\begin{equation}
r_8=\frac{s}{\sqrt{2}}.
\end{equation}
El campo eléctrico total vendrá dado por el principio de superposición como
\begin{equation}
\vec{E}=\sum_{i=1}^{8}\vec{E}_i,
\end{equation}
donde \(\vec{E}_i \) es el campo eléctrico producido por la carga puntual \(i \). Usando la expresión explícita en la ecuación \eqref{efield} en la ecuación anterior, obtenemos
\begin{equation}
\vec{E}=\sum_{i=1}^{8}\frac{1}{4\pi\epsilon_0}\frac{q}{r_i^3}\vec{r}_i,
\end{equation}
donde podemos sacar los términos constantes de la suma para obtener
\begin{equation}
\label{efield2}
\vec{E}=\frac{q}{4\pi\epsilon_0}\sum_{i=1}^{8}\frac{\vec{r}_i}{r_i^3}.
\end{equation}
A partir de la simetría del problema, el campo eléctrico en el plano XZ se cancela mientras que el campo eléctrico en el plano Y siempre se suma. Tomemos, por ejemplo, las cargas puntuales 3, 4, 7 y 8 que están a la misma distancia \(r \) del punto P. Vamos a sumar la razón encontrada en la ecuación \eqref{efield2}; a saber,
\begin{equation}
\frac{\vec{r}_3}{r_3^3}+\frac{\vec{r}_4}{r_4^3}+\frac{\vec{r}_7}{r_7^3}+\frac{\vec{r}_8}{r_8^3}.
\end{equation}
Como \(r_3=r_4=r_7=r_8\), podemos escribir
\begin{equation}
\label{3478}
\frac{\vec{r}_3}{r_3^3}+\frac{\vec{r}_4}{r_4^3}+\frac{\vec{r}_7}{r_7^3}+\frac{\vec{r}_8}{r_8^3}=\frac{\vec{r}_3+\vec{r}_4+\vec{r}_7+\vec{r}_8}{r_3^3}.
\end{equation}
Calculando el numerador en el lado izquierdo de la ecuación anterior, obtenemos:
\begin{equation*}
\vec{r}_3+\vec{r}_4+\vec{r}_7+\vec{r}_8=\left(\frac{s}{2}\,\hat{\textbf{i}}-\frac{s}{2}\,\hat{\textbf{k}}\right)+\left(-\frac{s}{2}\,\hat{\textbf{i}}-\frac{s}{2}\,\hat{\textbf{k}}\right)
\end{equation*}
\begin{equation}
+\left(\frac{s}{2}\,\hat{\textbf{i}}+\frac{s}{2}\,\hat{\textbf{k}}\right)+\left(-\frac{s}{2}\,\hat{\textbf{i}}+\frac{s}{2}\,\hat{\textbf{k}}\right),
\end{equation}
\begin{equation}
\vec{r}_3+\vec{r}_4+\vec{r}_7+\vec{r}_8=\vec{0}.
\end{equation}
Por lo tanto, la ecuación \eqref{3478} se convierte en
\begin{equation}
\label{def1}
\frac{\vec{r}_3}{r_3^3}+\frac{\vec{r}_4}{r_4^3}+\frac{\vec{r}_7}{r_7^3}+\frac{\vec{r}_8}{r_8^3}=\vec{0},
\end{equation}
lo que significa que no contribuyen a la suma en \eqref{efield2}.
Entonces nos quedamos con la suma de las cargas puntuales 1, 2, 5 y 6; explícitamente,
\begin{equation}
\frac{\vec{r}_1}{r_1^3}+\frac{\vec{r}_2}{r_2^3}+\frac{\vec{r}_5}{r_5^3}+\frac{\vec{r}_6}{r_6^3}.
\end{equation}
Como \(r_1=r_2=r_5=r_6\), podemos escribir
\begin{equation}
\label{1256}
\frac{\vec{r}_1}{r_1^3}+\frac{\vec{r}_2}{r_2^3}+\frac{\vec{r}_5}{r_5^3}+\frac{\vec{r}_6}{r_6^3}=\frac{\vec{r}_1+\vec{r}_2+\vec{r}_5+\vec{r}_6}{r_1^3}.
\end{equation}
Calculando el numerador en el lado izquierdo de la ecuación anterior, obtenemos:
\begin{equation*}
\vec{r}_1+\vec{r}_2+\vec{r}_5+\vec{r}_6=\left(-\frac{s}{2}\,\hat{\textbf{i}}+s\,\hat{\textbf{j}}-\frac{s}{2}\,\hat{\textbf{k}}\right)+\left(\frac{s}{2}\,\hat{\textbf{i}}+s\,\hat{\textbf{j}}-\frac{s}{2}\,\hat{\textbf{k}}\right)
\end{equation*}
\begin{equation}
+\left(-\frac{s}{2}\,\hat{\textbf{i}}+s\,\hat{\textbf{j}}+\frac{s}{2}\,\hat{\textbf{k}}\right)+\left(\frac{s}{2}\,\hat{\textbf{i}}+s\,\hat{\textbf{j}}+\frac{s}{2}\,\hat{\textbf{k}}\right),
\end{equation}
\begin{equation}
\vec{r}_1+\vec{r}_2+\vec{r}_5+\vec{r}_6=4s\,\hat{\textbf{j}}.
\end{equation}
Por lo tanto, la ecuación \eqref{1256} se convierte en
\begin{equation}
\frac{\vec{r}_1}{r_1^3}+\frac{\vec{r}_2}{r_2^3}+\frac{\vec{r}_5}{r_5^3}+\frac{\vec{r}_6}{r_6^3}=\frac{4s}{r_1^3}\,\hat{\textbf{j}},
\end{equation}
que, después de usar la expresión explícita para \(r_1 \) dada en \eqref{r1}, se convierte en
\begin{equation}
\frac{\vec{r}_1}{r_1^3}+\frac{\vec{r}_2}{r_2^3}+\frac{\vec{r}_5}{r_5^3}+\frac{\vec{r}_6}{r_6^3}=\frac{4s}{\left(s\sqrt{\frac{3}{2}}\right)^3}\,\hat{\textbf{j}},
\end{equation}
\begin{equation}
\label{def2}
\frac{\vec{r}_1}{r_1^3}+\frac{\vec{r}_2}{r_2^3}+\frac{\vec{r}_5}{r_5^3}+\frac{\vec{r}_6}{r_6^3}=\frac{4}{s^2\left(\frac{3}{2}\right)^{3/2}}\,\hat{\textbf{j}}.
\end{equation}
La suma en la ecuación \eqref{efield2} se puede escribir explícitamente como
\begin{equation}
\sum_{i=1}^{8}\frac{\vec{r}_i}{r_i^3}=\frac{\vec{r}_1}{r_1^3}+\frac{\vec{r}_2}{r_2^3}+\frac{\vec{r}_3}{r_3^3}+\frac{\vec{r}_4}{r_4^3}+\frac{\vec{r}_5}{r_5^3}+\frac{\vec{r}_6}{r_6^3}+\frac{\vec{r}_7}{r_7^3}+\frac{\vec{r}_8}{r_8^3},
\end{equation}
o reagrupando
\begin{equation}
\sum_{i=1}^{8}\frac{\vec{r}_i}{r_i^3}=\left(\frac{\vec{r}_1}{r_1^3}+\frac{\vec{r}_2}{r_2^3}+\frac{\vec{r}_5}{r_5^3}+\frac{\vec{r}_6}{r_6^3}\right)+\left( \frac{\vec{r}_3}{r_3^3}+\frac{\vec{r}_4}{r_4^3}+\frac{\vec{r}_7}{r_7^3}+\frac{\vec{r}_8}{r_8^3}\right).
\end{equation}
Ahora podemos usar las expresiones explícitas para los términos en cada paréntesis dados por las ecuaciones \eqref{def1} y \eqref{def2} en la ecuación anterior para obtener
\begin{equation}
\label{suma}
\sum_{i=1}^{8}\frac{\vec{r}_i}{r_i^3}=\frac{4}{s^2\left(\frac{3}{2}\right)^{3/2}}\,\hat{\textbf{j}}.
\end{equation}
Finalmente, usando la expresión en la ecuación \eqref{suma} en la ecuación del campo eléctrico, la ecuación \eqref{efield2}, obtenemos
\begin{equation}
\vec{E}=\frac{q}{4\pi\epsilon_0}\frac{4}{s^2\left(\frac{3}{2}\right)^{3/2}}\,\hat{\textbf{j}}.
\end{equation}
Usando los valores numéricos en unidades SI (\(q=6\times10^{-6}\,\text{C}\) y \(s=0.25\,\text{m}\)), obtenemos
\begin{equation}
\vec{E}=\frac{6\times10^{-6}\,\text{C}}{4\pi(8.854\times10^{-12}\,\text{F/m})}\frac{4}{(0.25\,\text{m})^2\left(\frac{3}{2}\right)^{3/2}}\,\hat{\textbf{j}},
\end{equation}
\begin{equation}
\vec{E}\approx 1.88\times 10^{6}\,\text{N/C}\,\hat{\textbf{j}}.
\end{equation}
[/mepr-show]
You need to be registered and logged in to take this quiz. Log in

Leave A Comment