¡Grifo en el último piso!

Usa la ecuación de continuidad y la ecuación de Bernoulli para resolver la velocidad del grifo con un sistema de ecuaciones \(2 \times 2\).

La ecuación de continuidad establece:

\begin{equation*}
v_{\text{pipe}}A_{\text{pipe}}=v_{\text{faucet}}A_{\text{faucet}},
\end{equation*}

[mepr-show rules=”4409″ unauth=”both”]

donde el área son áreas circulares transversales, entonces \(A = \pi r^2\) que nos permite relacionar las velocidades. Para este problema, la ecuación de Bernoulli se puede escribir como:

\begin{equation*}
P_{\text{pipe}}+\frac{1}{2}\rho v^2_{\text{pipe}}+\rho g z_{\text{pipe}}=P_{\text{faucet}}+\frac{1}{2}\rho v^2_{\text{faucet}}+\rho g z_{\text{faucet}},
\end{equation*}

donde usando la relación de las velocidades y despejando \(v_{\text{faucet}}\) después de mucho álgebra obtenemos:

\begin{equation*}
v_{\text{faucet}}=\sqrt{\frac{2(P_{\text{pipe}}-P_0-\rho gh)}{\rho\left(1-\frac{ r_{\text{faucet}}^4}{r_{\text{pipe}}^4}\right) }}.
\end{equation*}

Con valores numéricos:

\begin{equation*}
v_{\text{faucet}} \approx 4.18 \, \text{m/s}.
\end{equation*}

Para obtener una explicación más detallada de cualquiera de estos pasos, haga clic en “Solución detallada”.

[/mepr-show]

Necesitamos encontrar la rapidez y la presión del agua en el último piso. Primero, observe que la presión \(P\) cuando el agua sale de un grifo es la misma que la del entorno, por lo tanto, la presión en el grifo es la presión atmosférica \(P_0=101325\,\text{Pa}\).

Para resolver la rapidez debemos usar las ecuaciones de flujo estable: la ecuación de conservación de la masa y la ecuación de Bernoulli. Las ecuaciones de conservación de masa establecen que en cualquier punto de un flujo, la cantidad de masa \(m\) por unidad de tiempo \(t\) es siempre la misma. Es decir

\begin{equation}
\label{dmdt}
\frac{dm}{dt}=\text{constant}.
\end{equation}

[mepr-show rules=”4409″ unauth=”both”]

Escribiendo la masa \(m\) en términos de la densidad del fluido \(\rho\) y su volumen \(V\) como

\begin{equation}
m=\rho V,
\end{equation}

podemos reescribir la ecuación \eqref{dmdt} como

\begin{equation}
\label{flux}
\rho\frac{dV}{dt}=\text{constant}.
\end{equation}

Si la densidad del fluido es constante a lo largo de todo el flujo, entonces la cantidad que debe ser constante es el flujo

\begin{equation}
\label{flux2}
\frac{dV}{dt}=\text{constant}.
\end{equation}

Por lo tanto, el flujo en la entrada de la tubería debe ser el mismo en el grifo cuando está completamente abierto, es decir

\begin{equation}
\label{flux3}
\frac{dV}{dt}\Big|_{\text{pipe}}=\frac{dV}{dt}\Big|_{\text{faucet}}.
\end{equation}

Para un flujo estable, el flujo se puede calcular en cualquier punto como el producto de la velocidad del fluido \(v\) por el área transversal \(A\), es decir

\begin{equation}
\label{va}
\frac{dV}{dt}=vA.
\end{equation}

Usando la ecuación \eqref{va} en ambos lados de la ecuación \eqref{flux3} , obtenemos

\begin{equation}
\label{va2}
v_{\text{pipe}}A_{\text{pipe}}=v_{\text{faucet}}A_{\text{faucet}},
\end{equation}

donde \(v_{\text{pipe}}\) y \(v_{\text{faucet}}\) es la velocidad del agua al comienzo de las tuberías y en el grifo respectivamente. Los términos \(A_{\text{pipe}}\) y \(A_{\text{faucet}}\) son las áreas transversales de las tuberías y los grifos respectivamente. Debido a que ambas áreas transversales son circulares, se pueden calcular de acuerdo con la expresión

\begin{equation}
\label{area}
A=\pi r^2,
\end{equation}

donde \(r\) es el radio. Usando la ecuación \eqref{area} en la ecuación \eqref{va2} , obtenemos

\begin{equation}
v_{\text{pipe}}\pi r_{\text{pipe}}^2=v_{\text{faucet}}\pi r_{\text{faucet}}^2,
\end{equation}

donde podemos resolver \(v_{\text{pipe}}\) para obtener

\begin{equation}
v_{\text{pipe}}=\frac{v_{\text{faucet}}\pi r_{\text{faucet}}^2}{\pi r_{\text{pipe}}^2},
\end{equation}

que después de la simplificación se convierte en

\begin{equation}
\label{vfaucet}
v_{\text{pipe}}=\frac{v_{\text{faucet}} r_{\text{faucet}}^2}{ r_{\text{pipe}}^2}.
\end{equation}

La relación de velocidades dada en la ecuación \eqref{vfaucet} Será útil para resolver en la ecuación de Bernoulli. La ecuación de Bernoulli se aplica a flujos estables e irrotacionales e incompresibles, como el que tenemos. La ecuación dice que para cada punto de una línea de corriente

\begin{equation}
\label{bernoulli}
P+\frac{1}{2}\rho v^{2}+\rho g z=\text{constant},
\end{equation}

donde \(P\) es la presión absoluta en el fluido, \(v\) la velocidad del fluido a lo largo de la línea de corriente, \(z\) la altura del punto en la línea de corriente y \(g\) la aceleración gravitacional.

Luego podemos escribir la ecuación de Bernoulli para dos puntos en la misma línea de corriente, es decir, cuando el flujo ingresa a las tuberías y cuando el flujo sale del grifo. Luego, usando la ecuación \eqref{bernoulli} obtenemos

\begin{equation}
\label{ber2}
P_{\text{pipe}}+\frac{1}{2}\rho v^2_{\text{pipe}}+\rho g z_{\text{pipe}}=P_{\text{faucet}}+\frac{1}{2}\rho v^2_{\text{faucet}}+\rho g z_{\text{faucet}}.
\end{equation}

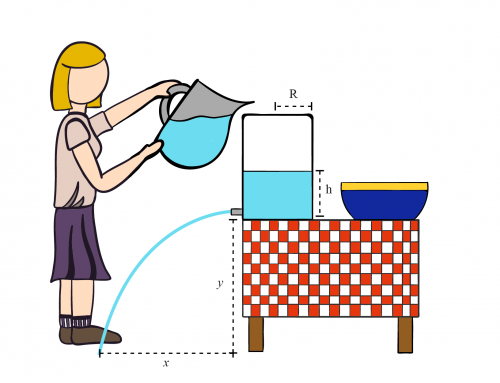
La presión \(P_{\text{pipe}}\) viene dada numéricamente por el problema mientras que la presión \(P_{\text{faucet}}\) es la presión atmosférica \(P_0\) debido al agua que sale al exterior. En la figura 1, vemos que en nuestro sistema de coordenadas, con origen en el piso, \(z_{\text{pipe}}=0\) y \(z_{\text{faucet}}\) es la altura del edificio \(h\).

Figura 1: Agua fluyendo a través de la tubería desde el nivel de la calle hasta el grifo abierto. La flecha indica la dirección del flujo. También se muestra la diferencia a lo largo del eje Z entre el nivel de la calle y el grifo.

Usando los resultados anteriores para simplificar la ecuación \eqref{ber2} , obtenemos

\begin{equation}
\label{ber3}
P_{\text{pipe}}+\frac{1}{2}\rho v_{\text{pipe}}^2=P_0+\frac{1}{2}\rho v_{\text{faucet}}^2+\rho g h,
\end{equation}

donde podemos usar el resultado de la ecuación \eqref{vfaucet} para escribir

\begin{equation}
\label{ber4}
P_{\text{pipe}}+\frac{1}{2}\rho \left(\frac{v_{\text{faucet}} r_{\text{faucet}}^2}{r_{\text{pipe}}^2}\right)^2=P_0+\frac{1}{2}\rho v_{\text{faucet}}^2 +\rho g h,
\end{equation}

donde la única incógnita es \(v_{\text{faucet}}\). Tomando todos los términos que involucran a \(v_{\text{faucet}}\) al lado derecho y todos los demás términos al lado izquierdo

\begin{equation}
P_{\text{pipe}}-P_0-\rho gh=\frac{1}{2}\rho v_{\text{faucet}}^2-\frac{1}{2}\rho \left(\frac{v_{\text{faucet}} r_{\text{faucet}}^2}{r_{\text{pipe}}^2}\right)^2,
\end{equation}

que después de evaluar el paréntesis se convierte explícitamente en

\begin{equation}
P_{\text{pipe}}-P_0-\rho gh=\frac{1}{2}\rho v_{\text{faucet}}^2-\frac{1}{2}\rho \frac{v_{\text{faucet}}^2 r_{\text{faucet}}^4}{r_{\text{pipe}}^4}.
\end{equation}

Después de factorizar los términos del lado derecho, podemos escribir

\begin{equation}
P_{\text{pipe}}-P_0-\rho gh=\frac{1}{2}\rho v_{\text{faucet}}^2\left(1-\frac{ r_{\text{faucet}}^4}{r_{\text{pipe}}^4}\right).
\end{equation}

Resolviendo para \(v_{\text{faucet}}\) en la ecuación anterior, obtenemos

\begin{equation}
v_{\text{faucet}}=\sqrt{\frac{2(P_{\text{pipe}}-P_0-\rho gh)}{\rho\left(1-\frac{ r_{\text{faucet}}^4}{r_{\text{pipe}}^4}\right) }}.
\end{equation}

Usando los valores numéricos en unidades SI, obtenemos

\begin{equation}
v_{\text{faucet}}=\sqrt{\frac{2(6\times 10^{5}\,\text{Pa}-101325\,\text{Pa}-(1000\,\text{kg/m}^2)(9.81\,\text{m/s}^2)(50\,\text{m}))}{1000\,\text{kg/m}^3\left(1-\frac{(2\,\text{cm})^4}{(4\,\text{cm})^4}\right)}},
\end{equation}

\begin{equation}
v_{\text{faucet}}\approx 4.18 \,\text{m/s}.
\end{equation}

[/mepr-show]

You need to be registered and logged in to take this quiz. Log in