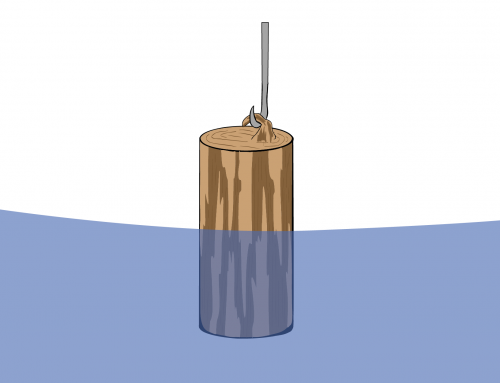
Un corcho con una masa de 35 g se sumerge en agua y se sujeta con una balanza de resorte en el fondo del recipiente, como se muestra en la figura. Si la escala lee 110 g, ¿cuál es la densidad del corcho?
Utilice la segunda ley de Newton y considere que la lectura en la escala de la masa es solo una “fuerza normal”.
Según la segunda ley de Newton en equilibrio, tenemos:
\begin{equation*}
\sum F = 0,
\end{equation*}
[mepr-show rules=”4409″ unauth=”both”]
que en este caso obtenemos:
\begin{equation*}
F_B – N – mg = 0,
\end{equation*}
donde \(N = m_s g\) y \(F_B = \rho_f V g\). En este caso, el volumen sumergido se puede escribir como:
\begin{equation*}
V = \frac{m}{\rho_c}.
\end{equation*}
Reemplazando esas variables y resolviendo \(\rho_c\) después de algo de álgebra, obtenemos:
\begin{equation*}
\rho_c=\rho_f \frac{m}{m+m_s},
\end{equation*}
que con valores numéricos es:
\begin{equation*}
\rho_c \approx 241.4 \, \text{kg/m}^3.
\end{equation*}
Para obtener una explicación más detallada de cualquiera de estos pasos, haga clic en “Solución detallada”.
[/mepr-show]
Necesitamos encontrar la densidad del corcho. Notamos que este es un problema de equilibrio de fuerzas, por lo que identificaremos todas las fuerzas presentes en el corcho y luego usaremos la segunda ley de Newton, junto con el principio de Arquímedes, para resolver la densidad del corcho.
Primero, dibujemos el diagrama de cuerpo libre para el corcho, como se ve en la figura 1. Las tres fuerzas ejercidas sobre el corcho son el peso \(\vec{W}\), la fuerza de flotación \(\vec{F} _B\), y la fuerza de contacto del corcho con la escala de resorte \(\vec{N}\).
[mepr-show rules=”4409″ unauth=”both”]
Figura 1: diagrama de cuerpo libre del corcho. El sistema de coordenadas está orientado de manera que el eje Y apunte hacia arriba. Se muestran tres fuerzas ejercidas sobre el corcho: la fuerza de flotación \(\vec{F}_B\), el peso \(\vec{W}=-mg\,\hat{\textbf{j}}\), y la fuerza de contacto ejercida por la balanza sumergida \(\vec{N}\).
La dirección del peso y la fuerza de flotación es evidente por su naturaleza. La dirección de la fuerza de contacto \(\vec{N}\) es tal que evita que el corcho suba.
Para el caso estático, la aceleración del corcho es cero, \(\vec{a}=\vec{0}\), por lo que podemos escribir la segunda ley de Newton como
\begin{equation}
\sum \vec{F}=m\vec{a},
\end{equation}
\begin{equation}
\label{newton}
\sum \vec{F}=\vec{0},
\end{equation}
donde \(m\) es la masa del corcho y \(\sum \vec{F}\) es la suma de todas las fuerzas ejercidas sobre el corcho. En términos de las fuerzas que se muestran en la figura 1, podemos escribir la ecuación \eqref{newton} como
\begin{equation}
\label{newton2}
\vec{F}_B+\vec{W}+\vec{N}=\vec{0}.
\end{equation}
A partir del sistema de coordenadas establecido en la figura 1, el peso se dirige en la dirección Y negativa, su magnitud es \(mg\), donde \(g\) es la aceleración gravitacional, por lo tanto
\begin{equation}
\label{w}
\vec{W}=-mg\,\hat{\textbf{j}}.
\end{equation}
La fuerza de flotación se dirige hacia arriba, hacia el eje Y positivo, y con magnitud, según el principio de Arquímedes \(\rho_f V _{\text{sub}}g\). Por lo tanto:
\begin{equation}
\label{fb}
\vec{F}_B=\rho_f V_{\text{sub}}g\,\hat{\textbf{j}},
\end{equation}
donde \(\rho_f\) es la densidad del fluido en el que se sumerge el corcho y \(V_{\text{sub}}\) es el volumen del corcho sumergido. En nuestro caso, el volumen sumergido es el volumen total del corcho, una variable desconocida. Sin embargo, podemos relacionar el volumen total con la masa, una variable conocida, a través de la densidad del corcho \(\rho_c\) de la siguiente manera
\begin{equation}
\rho_c=\frac{m}{V},
\end{equation}
que resolviendo para \(V\), el volumen total, se convierte en
\begin{equation}
\label{volu}
V=\frac{m}{\rho_c}.
\end{equation}
Usando la expresión para \(V\) de la ecuación \eqref{volu} en la ecuación \eqref{fb} , obtenemos
\begin{equation}
\label{fb2}
\vec{F}_B=\rho_f\frac{m}{\rho_c}g\,\hat{\textbf{j}}.
\end{equation}
La fuerza de contacto \(\vec{N}\) tiene una magnitud denotada por \(N\), y su dirección es hacia abajo, por lo que podemos escribir
\begin{equation}
\label{ene}
\vec{N}=-N\,\hat{\textbf{j}}.
\end{equation}
La magnitud \(N\) es igual al valor de masa informado por la balanza de resorte \(m_{s}\) multiplicado por la aceleración gravitacional \(g\). Recuerde que todas las balanzas miden fuerza, no masa. La constante de equivalencia siempre es la aceleración de la gravedad en el caso estático. Entonces, podemos escribir la ecuación \eqref{ene} como
\begin{equation}
\label{ene2}
\vec{N}=-m_sg\,\hat{\textbf{j}}.
\end{equation}
Usando las expresiones explícitas para las tres fuerzas dadas en las ecuaciones \eqref{w} , \eqref{fb2} y \eqref{ene2} en la ecuación \eqref{newton2} obtenemos,
\begin{equation}
\rho_f\frac{m}{\rho_c}g\,\hat{\textbf{j}}-mg\,\hat{\textbf{j}}-m_sg\,\hat{\textbf{j}}=\vec{0}.
\end{equation}
Dado que todas las fuerzas están a lo largo del eje Y, podemos omitir el vector unitario \(\hat{\textbf{j}}\) y escribir
\begin{equation}
\rho_f\frac{m}{\rho_c}g-mg-m_sg=0,
\end{equation}
donde podemos cancelar el factor \(g\) para obtener
\begin{equation}
\rho_f\frac{m}{\rho_c}-m-m_s=0.
\end{equation}
Resolviendo para el término que contiene \(\rho_c\), tenemos
\begin{equation}
\rho_f\frac{m}{\rho_c}=m+m_s,
\end{equation}
donde podemos intercambiar el lugar de \(\rho_c\) y \(m+m_s\) para finalmente obtener
\begin{equation}
\rho_c=\rho_f \frac{m}{m+m_s}.
\end{equation}
Podemos usar los valores numéricos dados para obtener
\begin{equation}
\rho_c=(1000\,\text{kg/m}^3)\frac{35\,\text{g}}{35\,\text{g}+110\,\text{g}},
\end{equation}
\begin{equation}
\rho_c\approx 241.4\,\text{kg/m}^3.
\end{equation}
[/mepr-show]
You need to be registered and logged in to take this quiz. Log in


Leave A Comment