¡Ciclista!

(a) Utilice la ecuación que da la posición de un objeto que se mueve con aceleración constante y recuerde que la aceleración se puede escribir en función de la velocidad.

(b) Use la ecuación de movimiento tanto para la ciclista como para la pelota para trazar sus posiciones en función del tiempo.

(a) La ciclista alcanza el balón de fútbol después de viajar 20 metros, por lo que el tiempo en el que la ciclista llega al balón (que es lo que necesitamos encontrar) es equivalente al tiempo en el que la ciclista viaja 20 metros. Y para encontrar este tiempo, necesitamos encontrar su ecuación de movimiento:

\begin{equation*}
\vec{x}_f = \frac{1}{2} \vec{a} t^2 + \vec{v}_i t + \vec{x}_i.
\end{equation*}

Nos dicen que después de 20 metros, la ciclista no solo está detrás de la pelota, sino que también tiene la misma rapidez (que es \(3 \, \text{m/s}\)). Esta información es útil para relacionar la aceleración y el tiempo. En general, la aceleración de un objeto viene dada por

\begin{equation*}
\vec{a} = \frac{\vec{v}_f – \vec{v}_i}{t}.
\end{equation*}

Usando la última ecuación en la primera y despejando \(t\) obtenemos:

\begin{equation*}
\frac{2 x_{fc}}{( v_f + v_{i} )} = t,
\end{equation*}

y con valores numéricos obtenemos:

\begin{equation*}
t = 1.74 \, \text{s}.
\end{equation*}

(b) Para hacer una gráfica de posición versus tiempo para ambos objetos, necesitamos considerar sus ecuaciones de movimiento. Recuerde que la ecuación de movimiento de los ciclistas, con aceleración negativa, es:

\begin{equation*}
x_{fc} = – \frac{1}{2} a t^2 + v_{i} t.
\end{equation*}

Para el balón de fútbol tiene rapidez constante, por lo que la ecuación de movimiento es:

\begin{equation*}
x_b = v_b t + x_i.
\end{equation*}

Por lo tanto, obtenemos:

Posición en función del tiempo para la ciclista (línea roja) y para el balón de fútbol (línea azul).

Para obtener una explicación más detallada de cualquiera de estos pasos, haga clic en “Solución detallada”.

(a) La ciclista alcanza el balón de fútbol después de viajar 20 metros, por lo que el tiempo en el que la ciclista llega al balón (que es lo que necesitamos encontrar) es equivalente al tiempo en el que la ciclista viaja 20 metros. Y para encontrar este tiempo, necesitamos encontrar su ecuación de movimiento.

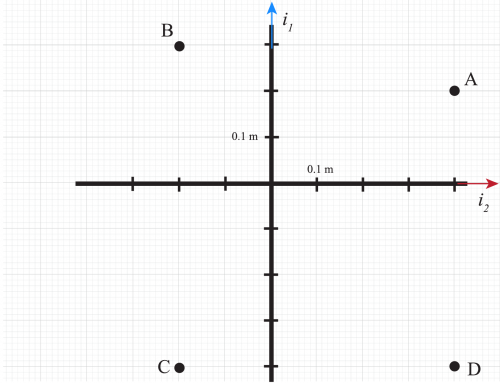
Para escribir la ecuación de movimiento, comencemos por elegir un sistema de coordenadas. Usaremos uno donde el origen está en la ubicación de la ciclista en el momento en que comienza a frenar, y donde el eje X positivo apunta en la dirección en la que se está moviendo.

Figura 1: Sistema de coordenadas para el problema.

Nos dicen que la ciclista empieza a frenar de forma constante. Esto significa que sigue un movimiento de aceleración constante y, por lo tanto, su ecuación de movimiento tiene la forma:

\begin{equation}
\vec{x}_f = \frac{1}{2} \vec{a} t^2 + \vec{v}_i t + \vec{x}_i,
\end{equation}

donde \(\vec{x}_f\) es la posición final, \(\vec{x}_i\) es la posición inicial, \(\vec{v}_i\) la velocidad inicial, \(a\) la aceleración y \(t\) el tiempo. En el contexto actual, según nuestro sistema de coordenadas, la aceleración es negativa porque la ciclista está frenando, la velocidad inicial es positiva en X, la posición final es positiva en X y la posición inicial es cero. Entonces, la ecuación de movimiento para la ciclista es

\begin{equation}
\label{Cyclist_xfGeneral}
x_{fc} \, \hat{\textbf{i}} = – \frac{1}{2} a t^2 \, \hat{\textbf{i}} + v_{i} t \, \hat{\textbf{i}} + 0 \, \hat{\textbf{i}}.
\end{equation}

Observe que conocemos \(v_i\) (es \(10\, \text{m/s}\)). Pero no sabemos la aceleración ni el tiempo. Entonces, para continuar, necesitamos más ecuaciones.

Nos dicen que después de 20 metros, la ciclista no solo está detrás de la pelota, sino que también tiene la misma rapidez (que es \(3 \, \text{m/s}\)). Esta información es útil para relacionar la aceleración y el tiempo. En general, la aceleración de un objeto viene dada por

\begin{equation}
\vec{a} = \frac{\vec{v}_f – \vec{v}_i}{t},
\end{equation}

donde \(\vec{v} _f\) es la velocidad final, \(\vec{v}_i\) el inicial y \(t\) el tiempo. O, usando vectores unitarios para todos los términos, tenemos

\begin{equation}
\label{Cyclist_aceleracionNegativaConGorro}
– a \, \hat{\textbf{i}} = \frac{v_f \, \hat{\textbf{i}} – v_i \, \hat{\textbf{i}}}{t},
\end{equation}

donde usamos el hecho de que, en el lado izquierdo, la aceleración es negativa en X según nuestro sistema. Si nos enfocamos solo en las magnitudes, obtenemos

\begin{equation}
– a = \frac{v_f – v_i }{t}.
\end{equation}

O de forma equivalente,

\begin{equation}
a = \frac{v_i – v_f }{t}.
\end{equation}

Observe que si no hubiéramos insertado el signo negativo delante de la aceleración en la ecuación \eqref{Cyclist_aceleracionNegativaConGorro} , entonces habríamos obtenido \(a = \frac{v_f – v_i}{t}\), que es un número negativo porque la rapidez final es menor que la rapidez inicial. Sería un error usar \(\frac{v_f – v_i}{t} \) para \(a\) en la ecuación \eqref{Cyclist_xfGeneral} porque en esta ecuación ya tomamos en cuenta la dirección negativa de la aceleración (por eso hay un signo menos delante de \(1/2\). La lección es que si tenemos en cuenta la dirección de un vector en algún punto (por ejemplo, como hicimos en la ecuación \eqref{Cyclist_xfGeneral}), debemos ser consistentes y tener en cuenta la dirección en todas las demás ecuaciones también (como en la ecuación \eqref{Cyclist_aceleracionNegativaConGorro}).

Usemos este resultado en la ecuación \eqref{Cyclist_xfGeneral}. Obtenemos que

\begin{equation}
x_{fc} \, \hat{\textbf{i}} = – \frac{1}{2} \left( \frac{v_i – v_f }{t} \right) t^2 \, \hat{\textbf{i}} + v_{i} t \, \hat{\textbf{i}}.
\end{equation}

Observe que un factor de \(t\) se cancela, por lo que obtenemos

\begin{equation}
x_{fc} \, \hat{\textbf{i}} = – \frac{1}{2} (v_i – v_f) t \, \hat{\textbf{i}} + v_{i} t \, \hat{\textbf{i}} .
\end{equation}

Los dos términos con \(v_i\) se pueden sumar y obtenemos

\begin{equation}
x_{fc} \, \hat{\textbf{i}} = \frac{1}{2} v_f t \, \hat{\textbf{i}} + \frac{1}{2} v_{i} t \, \hat{\textbf{i}}.
\end{equation}

Hemos llegado a una ecuación para la ciclista que solo tiene una variable desconocida, a saber, el tiempo. Entonces, podemos encontrar el tiempo a partir de esta ecuación. Primero, centrémonos solo en las magnitudes y tomemos el factor común de \(t\):

\begin{equation}
x_{fc} = \left( \frac{1}{2} v_f + \frac{1}{2} v_{i} \right) t .
\end{equation}

Ahora, multiplicamos ambos lados por 2 para obtener

\begin{equation}
2 x_{fc} = ( v_f + v_{i} ) t.
\end{equation}

Finalmente, dividimos por \(( v_f + v_{i})\) Llegar

\begin{equation}
\frac{2 x_{fc}}{( v_f + v_{i} )} = t.
\end{equation}

Ahora, insertamos los valores numéricos:

\begin{equation}
\frac{2 (20 \, \text{m})}{(3 \, \text{m/s}) + (20 \, \text{m/s})} = t,
\end{equation}

para obtener

\begin{equation}
t = 1.74 \, \text{s}.
\end{equation}

(b) Para hacer una gráfica de posición versus tiempo para ambos objetos, necesitamos considerar sus ecuaciones de movimiento nuevamente. Recuerde que la ecuación de movimiento de los ciclistas es

\begin{equation}
\label{Cyclist_xfGeneral2}
x_{fc} = – \frac{1}{2} a t^2 + v_{i} t.
\end{equation}

Ésta es la ecuación de una parábola que se abre hacia abajo debido al signo menos delante de \(1/2\). Cuando \(t = 0\), obtenemos \(x_{fc} = 0\), por lo que la parábola comienza en el origen. Además, en \(t=0\) hay una velocidad positiva inicial, por lo que la parábola tiene que empezar a subir en lugar de bajar inmediatamente. Poniendo todas estas cosas juntas, para la ciclista obtenemos (graficamos cuatro segundos):

Figura 2: Posición en función del tiempo para la ciclista. Observe que el movimiento es una parábola y se abre hacia abajo.

Aquí, el punto máximo de la parábola es el momento en el que la ciclista se detiene por completo (cuando su velocidad es cero). Si asumimos que la ciclista mantiene la misma aceleración negativa incluso después de detenerse, entonces comenzará a ir “hacia atrás” (en reversa), por lo que la parábola vuelve a bajar (acercándose a la posición inicial).

Para el balón de fútbol, la trama es muy fácil porque tiene una rapidez constante, por lo que la ecuación de movimiento es

\begin{equation}
x_b = v_b t + x_i,
\end{equation}

donde \(x_i\) es la posición inicial (que es positiva según nuestro sistema de coordenadas). Esta es la ecuación de una línea recta con pendiente positiva (porque la velocidad es positiva) que corta el eje Y en \(x_i\) (porque \(x_b=x_i\) cuando \(t=0\)). Por lo tanto, obtenemos

Figura 3: Posición en función del tiempo para la ciclista (línea roja) y para el balón de fútbol (línea azul).

Observe que en el momento en que la ciclista alcanza el balón de fútbol, sus rapideces son las mismas, por lo que debemos asegurarnos de que la pendiente de la parábola en ese punto coincida con la pendiente de la línea recta.