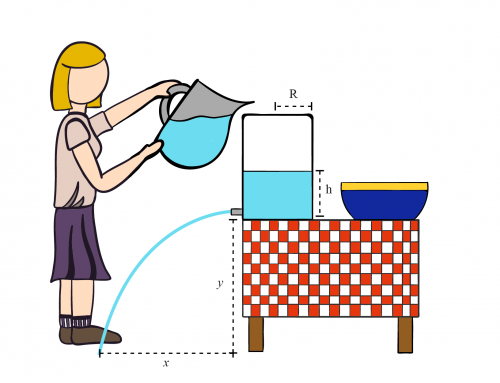
Lo han contratado para construir una fuente en un parque. El agua debe salir en un ángulo de 45 grados desde el suelo y alcanzar una altura de dos metros. Para lograr esto, la fuente debe tener una cámara de presión a una altura de 1 m sobre el nivel del suelo (ver el diagrama). ¿Cuál debe ser la presión en la cámara para lograr la altura deseada?
Con ecuaciones cinemáticas, encuentre la velocidad inicial conociendo la altura máxima que puede alcanzar el agua. Luego, según la ecuación de Bernoulli, encuentre la presión en el punto A.
Por la ecuación cinemática para la posición:
\begin{equation*}
y = y_0 + v_0y t – \frac{1}{2} g t^2,
\end{equation*}
[mepr-show rules=”4409″ unauth=”both”]
y
\begin{equation*}
v_y = v_0y \, – g t,
\end{equation*}
donde usando las condiciones para la altura máxima alcanzada, podemos encontrar el tiempo para la segunda ecuación y reemplazarlo en la primera. Luego, después de algo de álgebra, despejando \(v_0^2\) obtenemos:
\begin{equation*}
v_0^2 = \frac{2 g H }{ \cos^2 \theta}.
\end{equation*}
Entonces, la ecuación de Bernoulli dice:
\begin{equation*}
P_A + \frac{1}{2} \rho v_A^2 + \rho g y_A = P_B + \frac{1}{2} \rho v_B^2 + \rho g y_B.
\end{equation*}
Usando las condiciones dadas y la velocidad encontrada anteriormente, despejando \(P_A\) después de algo de álgebra, obtenemos:
\begin{equation*}
P_A = P_0 + \rho g \frac{H}{ \cos^2 \theta \, – h},
\end{equation*}
que con valores numéricos es:
\begin{equation*}
P_A = 1.3 \times 10^5 \ \text{Pa}.
\end{equation*}
Para obtener una explicación más detallada de cualquiera de estos pasos, haga clic en “Solución detallada”.
[/mepr-show]
Nos piden que averigüemos cuál debe ser la presión en la cámara de 1 m de altura para que el agua alcance los 2 m por encima del suelo. Podemos dividir la solución en dos partes. Primero, tenemos la parte hidrodinámica del problema, que describirá el movimiento del agua desde la bomba de presión hasta la salida de la fuente. A partir de esto, podemos obtener una expresión que relaciona la presión de la bomba con la velocidad del agua en la salida. El segundo paso involucra la cinemática, y modelaremos el agua como una partícula que experimenta un movimiento parabólico. A partir de esto, podemos calcular la velocidad inicial del movimiento, que es precisamente la velocidad del agua en la salida de la tubería.
[mepr-show rules=”4409″ unauth=”both”]
Figura 1: Fuente vertiendo agua donde hemos colocado el sistema de coordenadas en el suelo. En la parte izquierda del dibujo, vemos la cámara a una altura \(h\). El agua fluye por la tubería negra hasta que sale con una velocidad \(\vec{v}_i\) en un ángulo \(\theta\) y alcanza una altura máxima \(H\) en su movimiento parabólico.
Para la parte hidrodinámica de la solución, podemos usar la ecuación de Bernoulli para relacionar los puntos A (bomba) y B (salida) dentro de la tubería, dado que se supone que el movimiento del agua es ideal y se puede despreciar cualquier pérdida de energía mecánica.
Figura 2: El punto A es donde la cámara a una altura \(h\) está a una presión \(P_A\) mientras que en el punto B sale agua con una velocidad \(\vec{v}_I\) a presión atmosférica \(P_0\).
La ecuación de Bernoulli se puede escribir como
\begin{equation}
\label{Bernoulli1}
P_A + \frac{1}{2} \rho v_A^2 + \rho g y_A = P_B + \frac{1}{2} \rho v_B^2 + \rho g y_B.
\end{equation}
Como se muestra en el diagrama anterior, el agua comienza en reposo dentro de la bomba, por lo tanto \(v_A=0\), a una altura \(y_A = h = 1 m\). En el punto B (en el suelo \(y_B = 0\)) alcanza una velocidad \(v_B = v_0\), aún desconocida. La presión en el punto A es precisamente la cantidad que necesitamos encontrar, mientras que la presión en B es la presión atmosférica \(P_0\), dado que este punto está abierto a la atmósfera. Este razonamiento produce
\begin{equation}
\label{Bernoulli2}
P_A + 0 + \rho g h = P_0 + \frac{1}{2} \rho v_0^2 + 0.
\end{equation}
Tomando el término gravitacional de la izquierda al lado derecho
\begin{equation}
\label{Bernoulli3}
P_A = P_0+ \frac{1}{2} \rho v_0^2 – \rho g h,
\end{equation}
y factorizando \(\rho\), obtenemos
\begin{equation}
\label{Bernoulli3a}
P_A = P_0+ \rho\left( \frac{1}{2} \rho v_0^2 – g h\right).
\end{equation}
La expresión para \(P_A\) no se puede calcular todavía, ya que todavía no conocemos \(v_0\). Entonces, pasemos a la segunda parte de la solución, que involucra cinemática y nos permitirá encontrar una expresión para \(v_0\) en términos de parámetros conocidos.
Figura 3: En el punto C, donde la corriente de agua alcanza su altura máxima \(H\) la velocidad es horizontal \(\vec{v}_{ix} \).
En la figura 3 mostramos el punto inicial de la parábola, el punto B y el punto C de altura máxima. El agua comienza con velocidad \(v_0\) dirigida \(45^o\) por encima de la horizontal, produciendo los componentes de la velocidad en cada dirección como se muestra. En su altura máxima, el agua solo tendrá velocidad en la dirección x, por lo tanto \(v_cy = 0\).
Recordamos la ecuación cinemática para la componente y del movimiento parabólico
\begin{equation}
\label{ykinematics}
y = y_0 + v_0y t – \frac{1}{2} g t^2,
\end{equation}
y su derivada, la componente y de la velocidad
\begin{equation}
\label{vykinematics}
v_y = v_0y \, – g t.
\end{equation}
Luego, en ambas ecuaciones, reemplazamos la altura en C, \(y = H\), la altura inicial, \(y_0 = 0\), y el componente inicial de la velocidad , \(v_{0y} = v_0 \cos \theta \), obteniendo
\begin{equation}
\label{ykinematics2}
H = 0 + v_0 \cos \theta t – \frac{1}{2} g t^2,
\end{equation}
y
\begin{equation}
\label{vykinematics2}
0 = v_0 \cos \theta \, – g t,
\end{equation}
donde usamos el hecho de que el componente velocidad en C es cero. Como no conocemos el tiempo \(t\), lo eliminaremos de ambas ecuaciones. Tomamos el término de resta a la derecha de la ecuación \eqref{vykinematics2} hacia su lado izquierdo
\begin{equation}
\label{time1}
gt = v_0 \cos \theta,
\end{equation}
y dividimos por la gravedad
\begin{equation}
\label{time2}
t = v_0\frac{\cos \theta}{g}.
\end{equation}
Reemplazando esto en \eqref{ykinematics2} , tenemos
\begin{equation}
\label{maximumheight1}
H = v_0 \cos \theta \left(v_0\frac{\cos \theta}{g}\right) – \frac{1}{2} g \left(v_0\frac{\cos \theta}{g}\right)^2
\end{equation}
operando
\begin{equation}
\label{maximumheight2}
H = v_0^2 \frac{\cos^2 \theta}{g} – \frac{1}{2} g \left(v_0^2 \frac{\cos^2 \theta}{g}^2\right),
\end{equation}
anulando una gravedad en el último término, tenemos
\begin{equation}
\label{maximumheight3}
H = v_0^2 \frac{\cos^2 \theta}{g} – \frac{1}{2} \left(v_0^2 \frac{\cos^2 \theta}{g}\right),
\end{equation}
que nos da
\begin{equation}
\label{maximumheight4}
H = v_0^2 \frac{\cos^2 \theta}{ 2g}.
\end{equation}
Observe que sabemos todo en esta expresión, excepto la velocidad \(v_0\), que es precisamente lo que necesitamos para calcular la presión de la bomba. Luego, pasamos \(2g\) para multiplicar en el lado izquierdo
\begin{equation}
\label{v0}
2 g H = v_0^2 \cos^2 \theta,
\end{equation}
y dividimos por \(\cos^2 \theta\)
\begin{equation}
\label{v0-2}
\frac{2 g H }{ \cos^2 \theta }= v_0^2.
\end{equation}
Entonces podemos reemplazar la ecuación \eqref{v0-2} en \eqref{Bernoulli3}
\begin{equation}
\label{Pressure1}
P_A = P_0 + \rho (\frac{1}{2}(2 g H / \cos^2 \theta) – g h).
\end{equation}
Ahora cancelamos los 2, obteniendo
\begin{equation}
\label{Pressure2}
P_A = P_0 + \rho \frac{g H} { \cos^2 \theta \, – g h},
\end{equation}
luego factorizamos la gravedad, finalmente obteniendo
\begin{equation}
\label{Pressure3}
P_A = P_0 + \rho g \frac{H}{ \cos^2 \theta \, – h},
\end{equation}
donde conocemos todos los parámetros. Por lo tanto, reemplazamos todas las cantidades conocidas
\begin{equation}
\label{Pressure4}
P_A = 1.01 \times 10^5 \ \text{Pa} + \left(1000 \ \frac{\text{kg}}{\text{m}^3}\right) \left(10 \ \frac{\text{m}}{\text{s}^2}\right) \left(\frac{2\ \text{m}}{\frac{1}{2}} – 1 \ \text{m}\right),
\end{equation}
obteniendo
\begin{equation}
\label{PressureNum}
P_A = 1.3 \times 10^5 \ \text{Pa} \approx 1.3 \ \text{atm}.
\end{equation}
Por lo tanto, para que la fuente funcione como se propone, la presión de la bomba debe ser aproximadamente 30 \(\%\) más que la de la atmósfera al nivel del mar.
[/mepr-show]
You need to be registered and logged in to take this quiz. Log in


Leave A Comment