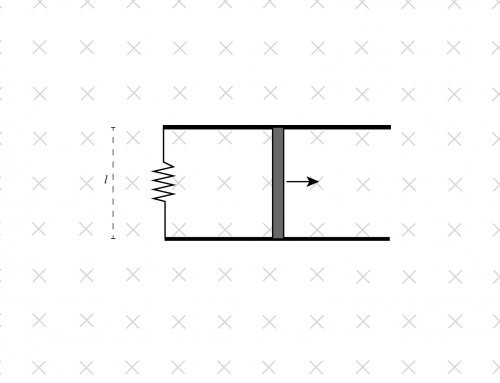
En algún instante, un protón se mueve a una rapidez \(v \) perpendicular a un campo eléctrico de magnitud \(E \), como se muestra en la figura. Si desea utilizar un campo magnético uniforme para hacer que el protón se mueva siempre en línea recta y con una rapidez constante, ¿en qué dirección debe ir el campo y cuál debe ser su magnitud? Desprecie el peso del protón, ya que es demasiado pequeño en comparación con las otras fuerzas.
Utilice la segunda ley de Newton para determinar dónde se necesita la fuerza magnética en equilibrio. La definición de fuerza magnética debería darle la dirección del campo magnético.
Escribiendo la Segunda Ley de Newton en equilibrio, obtenemos:
\begin{equation*}
\sum F = 0.
\end{equation*}
[mepr-show rules=”4409″ unauth=”both”]
Entonces:
\begin{equation}
F_E – F_B = 0,
\end{equation}
entonces las fuerzas deben ser las mismas, ya que \(F_E = qE \) y \(F_B = qvB \).
Despejando \(B \), obtenemos:
\begin{equation}
B = \frac{E}{v}.
\end{equation}
Si la velocidad está en la dirección \({y-} \) y el campo eléctrico está en la dirección \({z-} \), el campo magnético debe apuntar a lo largo del eje \({x-} \) de acuerdo con la regla de la mano derecha.
Para obtener una explicación más detallada de cualquiera de estos pasos, haga clic en “Solución detallada”.
[/mepr-show]
Según la segunda ley de Newton, un objeto solo se mueve en línea recta con velocidad constante si la fuerza neta sobre el objeto es cero (si la fuerza neta no fuera cero, entonces el protón estaría cambiando su velocidad o su dirección de movimiento) . Por lo tanto, para que el protón se mueva en línea recta con rapidez constante \({v} \), la fuerza neta ejercida sobre el protón debe ser cero. Debemos usar esta condición, junto con las expresiones de las fuerzas eléctricas y magnéticas, para encontrar el campo magnético.
Las únicas dos fuerzas que actúan sobre el protón son la fuerza eléctrica \(\vec{F}_E \), y la fuerza magnética \(\vec{F}_B \) (despreciamos el peso, como se indica en el enunciado). Dado que la fuerza total ejercida sobre el protón debe ser cero para que se mueva en línea recta con rapidez constante, obtenemos
\begin{equation}
\label{EQ:1}
\vec{F}_E + \vec{F}_B = 0.
\end{equation}
[mepr-show rules=”4409″ unauth=”both”]
Ahora, para continuar, debemos escribir estas fuerzas en términos de las variables que conocemos, a saber, el campo eléctrico, la carga del protón \(q = + e \) y la rapidez de esta partícula.
La fuerza eléctrica sobre una carga \(q \) debido a un campo eléctrico \(\vec{E} \) está dada por
\begin{equation}
\vec{F}_E = q\vec{E}.
\end{equation}
En nuestro caso, \(q = e \), obteniendo
\begin{equation}
\label{EQ:2}
\vec{F}_E = e\vec{E}.
\end{equation}
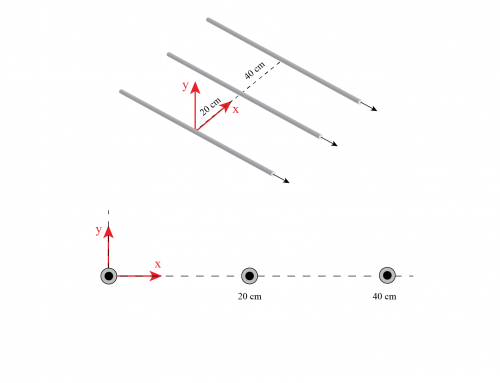
Elijamos ahora un sistema de coordenadas según el cual el electrón se mueve a lo largo del eje Y, y el campo eléctrico apunta en la dirección positiva de Z (somos libres de usar cualquier sistema de coordenadas que deseemos, y como veremos pronto, este es uno conveniente que se muestra en la figura 1).
Figura 1: Elegimos el sistema de coordenadas de modo que el protón se mueva a lo largo del eje Y y el campo eléctrico apunta hacia el eje Z positivo.
Según este sistema,
\begin{equation}
\vec{E} = E \, \hat{\textbf{k}}.
\end{equation}
Después de sustituir esto en \eqref{EQ:2}, obtenemos
\begin{equation}
\vec{F}_E = eE \, \hat{\textbf{k}}.
\end{equation}
Después de insertar esto en \eqref{EQ:1}, obtenemos
\begin{equation}
eE \, \hat{\textbf{k}} + \vec{F}_B = 0.
\end{equation}
Podemos reescribir esta ecuación como
\begin{equation}
\label{EQ:3}
\vec{F}_B = -eE \, \hat{\textbf{k}}.
\end{equation}
Por lo tanto, esta ecuación muestra que para que el protón mantenga una rapidez constante y se mueva en línea recta, debemos aplicar una fuerza magnética de magnitud \(eE \) que apunte en la dirección \(- \hat {\textbf{k} } \). Entonces, para continuar, debemos encontrar qué tipo de campo magnético produce este tipo particular de fuerza magnética.
Para encontrar el campo magnético \(B \) tal que la ecuación \eqref{EQ:3} sea satisfecha, debemos escribir la fuerza magnética en términos de \(\vec{B} \). La fuerza magnética sobre una carga \(q \) que se mueve con velocidad \(\vec{v} \) en una región con un campo magnético \(\vec{B} \) está dada por
\begin{equation}
\label{EQ:4}
\vec{F}_B = q \vec{v} \times \vec{B},
\end{equation}
donde esta expresión proviene de la parte magnética de la fuerza de Lorentz.
Usando el sistema de coordenadas que se muestra en la primera figura, podemos escribir la velocidad como \(\vec{v} = v \hat {\textbf{j} } \). Después de sustituir esto en la ecuación \eqref{EQ:4}, obtenemos
\begin{equation}
\vec{F}_B = qv \hat{\textbf{j}} \times \vec{B}.
\end{equation}
Ahora, si reemplazamos esto en la ecuación \eqref{EQ:3}, obtenemos
\begin{equation}
\label{EQ:5}
qv \hat{\textbf{j}} \times \vec{B} = -eE \, \hat{\textbf{k}}.
\end{equation}
Para encontrar \(\vec{B} \), debemos determinar su magnitud y dirección de manera que la ecuación \eqref{EQ:5} sea satisfecha. Podemos escribir \(\vec{B} = B \hat{u}\), donde \(B\) es la magnitud de \(\vec{B}\), y \(\hat{u}\) es un vector unitario que especifica su (todavía desconocida) dirección. Después de sustituir esto en la ecuación \eqref{EQ:5}, obtenemos
\begin{equation}
qv \hat{\textbf{j}} \times B\hat{u} = -eE \, \hat{\textbf{k}}.
\end{equation}
Si sacamos \(B \) del producto cruz (lo que siempre podemos hacer porque es un número), obtenemos
\begin{equation}
qvB \hat{\textbf{j}} \times \hat{u} = -eE \, \hat{\textbf{k}}.
\end{equation}
Esta es una igualdad entre vectores, por lo que tanto la magnitud como la dirección en cada lado deben ser iguales. En otras palabras,
\begin{equation}
\label{EQ:6}
qvB = eE
\end{equation}
debe ser válido para las magnitudes, y
\begin{equation}
\label{EQ:7}
\hat{\textbf{j}} \times \hat{u} = -\hat{\textbf{k}}
\end{equation}
debe satisfacerse para las direcciones.
Si dividimos la ecuación \eqref{EQ:6} por \(qv \), obtenemos que la magnitud de \(\vec{B} \) debe ser
\begin{equation}
\label{EQ:8}
B = \frac{eE}{qv}
\end{equation}
Finalmente, la dirección \(\hat{u} \) para \(\vec{B} \) debe satisfacer la ecuación \eqref{EQ:7}. Podemos encontrar esta dirección usando la regla de la mano derecha como se muestra en la figura 2.
Figura 2: Diagrama del campo magnético \(\vec{B} \) usando la regla de la mano derecha. Si la velocidad del protón está a lo largo de \(\hat {\textbf{j}} \) y la fuerza debe estar a lo largo de \(-\hat{\textbf{k} } \), entonces el campo magnético debe estar en la dirección \(\hat {\textbf{i}} \).
Por lo tanto, concluimos que \(\hat{u} = \hat{\textbf{i}}\). Poniendo esto junto con la magnitud de \(\vec{B} \) en \eqref{EQ:8} , y como \(q = e \), obtenemos que el campo magnético debe ser
\begin{equation}
\vec{B} = \frac{E}{v} \hat{\textbf{i}}.
\end{equation}[/mepr-show]


Leave A Comment