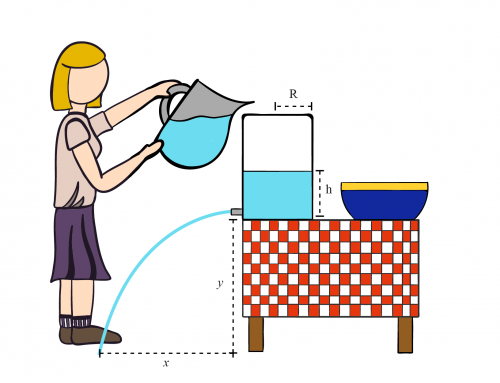
Agua y otro tipo de líquido se insertan en un tubo en forma de U que está abierto por ambos lados y tiene las dimensiones que se muestran en la figura.
(a) ¿Cuál es la densidad del líquido desconocido?
(b) Si el lado que contiene el líquido desconocido estuviera cerrado al vacío, ¿cuál sería su densidad?
(c) Si el lado del agua estuviera casi al vacío, ¿cuál sería la densidad del otro líquido? ¿Tiene sentido físico?
a) Aplicar la fórmula de presión a una altura donde la presión sea igual en ambos lados. Recuerde incluir o no la presión atmosférica.
b) La misma pista que la parte (a).
c) La misma pista que en a). Considere si el resultado tiene algún sentido.
a) En la interfaz, la presión absoluta debe ser la misma:
\begin{equation*}
P_w=P_u.
\end{equation*}
[mepr-show rules=”4409″ unauth=”both”]
En este caso:
\begin{equation*}
P_0+\rho_w g x= P_0+ \rho_u g h,
\end{equation*}
donde resolviendo para \(\rho_u\) obtenemos:
\begin{equation*}
\rho_u=\frac{\rho_w x}{h}.
\end{equation*}
Usando los valores numéricos, obtenemos
\begin{equation*}
\rho_u\approx 726.2\,\text{kg/m}^3.
\end{equation*}
b) Dado que un extremo está cerrado, obtenemos:
\begin{equation*}
P_0+\rho_w g x=\rho_u g h.
\end{equation*}
Resolviendo \(\rho_u\) en la ecuación anterior, tenemos
\begin{equation*}
\rho_u=\frac{P_0+\rho_w g x}{g h}.
\end{equation*}
Con valores numéricos:
\begin{equation*}
\rho_u = 3185.41\,\text{kg/m}^3.
\end{equation*}
c) Cerrado en el otro extremo:
\begin{equation*}
\rho_w g x=P_0+\rho_u g h.
\end{equation*}
Resolviendo para \(\rho_u\), tenemos
\begin{equation*}
\rho_u=\frac{-P_0+\rho_w g x}{g h}.
\end{equation*}
Con valores numéricos:
\begin{equation*}
\rho_u=-1733.04\,\text{kg/m}^3,
\end{equation*}
lo cual no tiene sentido ya que es un valor negativo.
Para obtener una explicación más detallada de cualquiera de estos pasos, haga clic en “Solución detallada”.
[/mepr-show]
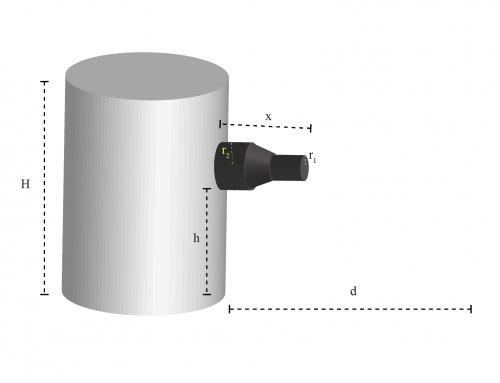
a) Necesitamos encontrar la densidad del líquido desconocido. Dibujemos nuevamente el manómetro de tubo en U primero, como se ve en la figura 1, donde hemos indicado las variables relevantes para resolver el problema.
[mepr-show rules=”4409″ unauth=”both”]
Figura 1: Tubo en forma de U abierto en ambos extremos. La presión en la superficie libre de ambos fluidos es la atmosférica \(P_0\). También se muestra la altura de la columna de ambos líquidos.
En ambos extremos tendremos la presión atmosférica \(P_0\). Para que los líquidos estén en equilibrio, la presión absoluta en la interfase debe ser la misma proveniente del agua y proveniente del fluido desconocido; llamaremos a estas presiones \(P_w\) y \(P_u\) respectivamente. Entonces, debemos tener
\begin{equation}
\label{principal}
P_w=P_u.
\end{equation}
Para calcular la presión absoluta debemos tener en cuenta que es la suma de varios términos. El primero de estos términos es la presión atmosférica, cuando está presente, y el segundo término es la presión hidrostática \(P_h\) dada por la expresión:
\begin{equation}
\label{hydrostatic}
P_h=\rho g y,
\end{equation}
donde \(\rho\) es la densidad del fluido, \(g\) es la aceleración gravitacional y \(y\) es la profundidad a la que se calcula la presión.
Por lo tanto, podemos escribir, usando la expresión dada en la ecuación \eqref{hydrostatic}
\begin{equation}
\label{pw}
P_w=P_0+\rho_w gx,
\end{equation}
donde \(x\) se define en la segunda figura y cuyo valor numérico se puede obtener de la primera figura como \(x=4.2\,\text{m}-1.15\text{m}=3.05\,\text{m}\). La densidad del agua se denota como \(\rho_w\)
Se puede hacer el mismo argumento para escribir
\begin{equation}
\label{pu}
P_u=\rho_u g h,
\end{equation}
donde \(\rho_u\) es la densidad del fluido desconocido y \(h\) es la profundidad en el fluido desconocido hasta la interfaz con el agua, como se ve en la figura 1.
Usando las expresiones explícitas para \(P_w\) y \(P_u\) dadas por las ecuaciones \eqref{pw} y \eqref{pu} en la ecuación \eqref{principal} , obtenemos
\begin{equation}
P_0+\rho_w g x= P_0+ \rho_u g h,
\end{equation}
donde podemos cancelar el término \(P_0\) para obtener
\begin{equation}
\label{p1}
\rho_w g x= \rho_u g h.
\end{equation}
Podemos resolver \(\rho_u\) a partir de la ecuación \eqref{p1} para obtener
\begin{equation}
\rho_u=\frac{\rho_w g x}{ g h},
\end{equation}
que tras la cancelación del término \(g\) se convierte en
\begin{equation}
\rho_u=\frac{\rho_w x}{h}.
\end{equation}
Usando los valores numéricos, obtenemos
\begin{equation}
\rho_u=\frac{(1000\,\text{kg/m}^3)(3.05\,\text{m})}{(4.2\,\text{m})},
\end{equation}
\begin{equation}
\rho_u\approx 726.2\,\text{kg/m}^3.
\end{equation}
Un valor cercano a la densidad de la gasolina, por ejemplo.
b) Ahora, el lado izquierdo está cerrado de manera que no haya aire entre la tapa y el fluido desconocido, pero las distancias dadas en la primera figura siguen siendo las mismas. Todavía podemos hacer el mismo análisis y usar la ecuación \eqref{principal} . La expresión para \(P_w\) es la misma pero en la expresión para \(P_u\) no tenemos que incluir el término para presión atmosférica, entonces
\begin{equation}
\label{pu2}
P_h=\rho_u g h.
\end{equation}
Usando el nuevo resultado de \(P_u\) y la expresión explícita para \(P_w\) dada en la ecuación \eqref{pw} en la ecuación \eqref{principal} , tenemos
\begin{equation}
P_0+\rho_w g x=\rho_u g h.
\end{equation}
Resolviendo \(\rho_u\) en la ecuación anterior, tenemos
\begin{equation}
\rho_u=\frac{P_0+\rho_w g x}{g h}.
\end{equation}
Usando los valores numéricos en unidades SI (\(P_0=101325\,\text{Pa}\), \(x=3.05\,\text{m}\), \(h=4.2\,\text{m}\) y \(g=9.81\,\text{m/s}^2\)), obtenemos
\begin{equation}
\rho_u=\frac{101325\,\text{Pa}+(1000\,\text{kg/m}^3)(9.81\,\text{m/s}^2)(3.05\,\text{m}) }{(9.81\,\text{m/s}^2)(4.2\,\text{m})},
\end{equation}
\begin{equation}
\rho_u=3185.41\,\text{kg/m}^3,
\end{equation}
que es casi el doble de la densidad del líquido más denso, Mercurio.
c) Ahora, el lado derecho está cerrado de manera que no haya aire entre la tapa y el agua, pero las distancias dadas en la figura 1 siguen siendo las mismas. Todavía podemos hacer el mismo análisis y usar la ecuación \eqref{principal} . La expresión para \(P_u\) es la misma que la ecuación \eqref{pu} , pero en la expresión para \(P_w\) no tenemos que incluir el término para la presión atmosférica, entonces
\begin{equation}
\label{pw2}
P_w=\rho_w g x.
\end{equation}
Usando el nuevo resultado de \(P_w\) y la expresión explícita para \(P_u\) dada en la ecuación \eqref{pu} en la ecuación \eqref{principal} , tenemos
\begin{equation}
\rho_w g x=P_0+\rho_u g h.
\end{equation}
Resolviendo \(\rho_u\) en la ecuación anterior, tenemos
\begin{equation}
\rho_u=\frac{-P_0+\rho_w g x}{g h}.
\end{equation}
Usando los valores numéricos en unidades SI (\(P_0=101325\,\text{Pa}\), \(x=3.05\,\text{m}\), \(h=4.2\,\text{m}\) y \(g=9.81\,\text{m/s}^2\)), obtenemos
\begin{equation}
\rho_u=\frac{-101325\,\text{Pa}+(1000\,\text{kg/m}^3)(9.81\,\text{m/s}^2)(3.05\,\text{m}) }{(9.81\,\text{m/s}^2)(4.2\,\text{m})},
\end{equation}
\begin{equation}
\rho_u=-1733.04\,\text{kg/m}^3,
\end{equation}
que es negativo. Debido a que todas las densidades deben ser valores positivos, concluimos que la situación propuesta en (c) es de naturaleza imposible. Las distancias \(x\) y \(h\) se reajustan cuando se cierra la tapa y se impone el vacío.
[/mepr-show]
You need to be registered and logged in to take this quiz. Log in


Leave A Comment