¡Potencial eléctrico dentro de un triángulo!

a) Use la fórmula del potencial eléctrico y encuentre las distancias de cada partícula al punto P.

b) Utilice el teorema de energía-trabajo.

a) El potencial eléctrico para una carga puntual es:

\begin{equation*}
V=\frac{1}{4\pi\epsilon_0}\frac{q}{r},
\end{equation*}

[mepr-show rules=”4409″ unauth=”both”]

donde se necesitan las distancias \(r \) para cada partícula.

Al colocar un sistema de coordenadas en el medio de la base del triángulo, las coordenadas del punto P son:

\begin{equation*}
\vec{P}=(0\,\text{cm}\,,\,2.58\,\text{cm}).
\end{equation*}

Las coordenadas de cada partícula están dadas por un vector \(\vec{A} _I\). Entonces, la distancia de cada partícula al punto P es la magnitud del siguiente vector:

\begin{equation*}
\vec{r}_i= \vec{A}_i – \vec{P}.
\end{equation*}

Entonces:

\begin{equation*}
r_1=0.0517\,\text{m},
\end{equation*}

\begin{equation*}
r_2 = 0.0326\,\text{m},
\end{equation*}

\begin{equation*}
r_3=0.0326\,\text{m}.
\end{equation*}

Al sumar el potencial eléctrico de las tres partículas obtenemos:

\begin{equation*}
V_P=\frac{1}{4\pi\epsilon_0}\frac{q_1}{r_1}+\frac{1}{4\pi\epsilon_0}\frac{q_2}{r_2}+\frac{1}{4\pi\epsilon_0}\frac{q_3}{r_3}.
\end{equation*}

Con valores numéricos:

\begin{equation*}
V_P \approx – 1.51 \times 10^{7} \, \text{V}.
\end{equation*}

b) El teorema trabajo-energía en términos de la energía eléctrica potencial que tenemos:

\begin{equation*}
W_{A\to B}=U_{A}-U_{B},
\end{equation*}

donde \(U = qV\). Entonces:

\begin{equation*}
W_{\infty\to P}=QV_{\infty}-QV_P.
\end{equation*}

Con \(V_{\infty} = 0\) y con valores numéricos obtenemos:

\begin{equation}
W_{\infty\to P}\approx 906\,\text{J}.
\end{equation}

Para obtener una explicación más detallada de cualquiera de estos pasos, haga clic en “Solución detallada”.

[/mepr-show]

a) El problema nos pide que encontremos el potencial eléctrico generado por las cargas en el punto P. Para resolver este problema, usaremos la definición de potencial eléctrico para una carga puntual y el principio de superposición. Para encontrar las distancias entre las cargas y el punto \(P \), se utilizará alguna geometría básica.

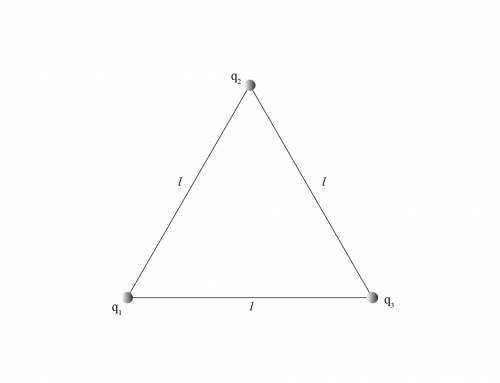
Comencemos dibujando el triángulo (ver figura 1), donde tomaremos \(q_1=q\) ,\(q_2=-q\) y \(q_3=-q\).

[mepr-show rules=”4409″ unauth=”both”]

Figura 1: Matriz triangular de cargas. Colocamos el sistema de coordenadas en el punto O a medio camino entre las cargas \(q_2 \) y \(q_3 \). También se muestra la distancia desde todas las cargas al punto P.

Las distancias \(r_1 \), \(r_2 \) y \(r_3 \) son las distancias entre cada carga y el punto \(P \), donde debemos calcular el potencial eléctrico \(V_P \).

Usando el principio de superposición, el potencial eléctrico \(V_P \) es la suma de los potenciales eléctricos debido a las cargas \(q_1 \), \(q_2 \) y \(q_3 \), que denotaremos como \(V_{1} \), \(V_2 \) y \(V_3 \), respectivamente. Explícitamente,

\begin{equation}
\label{sumV}
V_P=V_1+V_2+V_3.
\end{equation}

El potencial eléctrico producido por una carga puntual \(q \) a una distancia \(r \) está dado por

\begin{equation}
\label{vpunctual}
V=\frac{1}{4\pi\epsilon_0}\frac{q}{r},
\end{equation}

que es una cantidad escalar. La constante \(\epsilon_{0} \) se conoce como la permitividad del espacio libre y toma el valor \(\epsilon_0 = 8.854 \times 10^{-12}\,\text{F/m} \).
Usando la expresión dada en la ecuación \eqref{vpunctual} para escribir cada término en el lado derecho de la ecuación \eqref{sumV}, obtenemos

\begin{equation}
\label{vp}
V_P=\frac{1}{4\pi\epsilon_0}\frac{q_1}{r_1}+\frac{1}{4\pi\epsilon_0}\frac{q_2}{r_2}+\frac{1}{4\pi\epsilon_0}\frac{q_3}{r_3}.
\end{equation}

De la ecuación \eqref{vp}, podemos factorizar el término \(\frac{1}{4 \pi \epsilon_0} \) para obtener

\begin{equation}
\label{vp2}
V_P=\frac{1}{4\pi \epsilon_0}\left(\frac{q_1}{r_1}+\frac{q_2}{r_2}+\frac{q_3}{r_3}\right).
\end{equation}

Entonces, nos queda calcular las únicas incógnitas en la ecuación \eqref{vp2}, que son \(r_1 \), \(r_2 \) y \(r_3 \). Para calcular estas distancias, primero debemos calcular las coordenadas del punto \(P \). Tomando \(O \) como origen, las coordenadas para las cargas 2 y 3 son

\begin{equation}
\label{a2}
\vec{A_2}=(-2\,\text{cm}\,,\,0\,\text{cm}),
\end{equation}

\begin{equation}
\label{a3}
\vec{A_3}=(2\,\text{cm}\,,\,0\,\text{cm}),
\end{equation}

donde el subíndice de \(\vec{A} \) corresponde al número de la carga. Para la carga 1, conocemos su coordenada en X, que es cero, pero la coordenada en Y no viene dada por la figura 1; entonces, solo debemos dibujar la mitad derecha del triángulo y usar el teorema de Pitágoras para encontrar la altura; a saber,

\begin{equation}
y=\sqrt{(8\,\text{cm})^2-(2\,\text{cm})^2}\approx 7.75\,\text{cm}.
\end{equation}

Figura 2: Triángulo interior utilizado para calcular las coordenadas de carga \(q_1 \). La distancia vertical se obtiene mediante el teorema de Pitágoras.

entonces, las coordenadas de la carga 1 son

\begin{equation}
\vec{A_1}=(0\,\text{cm}\,,\,7.75\,\text{cm}).
\end{equation}

Como el punto \(P \) es el centro geométrico del triángulo, podemos calcular sus coordenadas como un promedio de las coordenadas de sus vértices. Es decir

\begin{equation}
\label{a1}
\vec{P}=\frac{\vec{A_1}+\vec{A_2}+\vec{A_3}}{3},
\end{equation}

que, después de usar las expresiones en las ecuaciones \eqref{a2}, \eqref{a3} y \eqref{a1}, se convierte en

\begin{equation}
\vec{P}=\frac{(0\,\text{cm}\,,\,7.75\,\text{cm})+(-2\,\text{cm}\,,\,0\,\text{cm})+(2\,\text{cm}\,,\,0\,\text{cm})}{3},
\end{equation}

\begin{equation}
\vec{P}=\frac{(0\,\text{cm}\,,\,7.75\,\text{cm})}{3},
\end{equation}

\begin{equation}\label{Pcoo}
\vec{P}=(0\,\text{cm}\,,\,2.58\,\text{cm}).
\end{equation}

Para encontrar \(r_1 \), necesitamos calcular las coordenadas \(\vec{r_1} \) y luego encontrar su magnitud. \(\vec{r_1} \) viene dado por la diferencia entre coordenadas \(\vec{A_1} \) y \(\vec{P} \). Usando \eqref{a1} y \eqref{Pcoo}, obtenemos

\begin{equation}
\vec{r_1}=\vec{A_1} – \vec{P}=(0\,\text{cm}\,,\,7.75\,\text{cm})-(0\,\text{cm}\,,\,2.58\,\text{cm}),
\end{equation}

que es equivalente a

\begin{equation*}
\vec{r_1}=(0\,\text{cm}-0\,\text{cm}\,,\,7.75\,\text{cm}-2.58\,\text{cm}),
\end{equation*}

\begin{equation}
\vec{r_1}=(0\,\text{cm}\,,\,5.17\,\text{cm}).
\end{equation}

Ahora, podemos calcular la magnitud del vector asociado a esta coordenada para encontrar \(r_1 \). Explícitamente

\begin{equation*}
r_1=|\vec{r_1}|,
\end{equation*}

\begin{equation*}
r_1=\sqrt{(0\,\text{cm})^2+(5.17\,\text{cm})^2},
\end{equation*}

\begin{equation}
\label{r1}
r_1=5.17\,\text{cm}=0.0517\,\text{m}.
\end{equation}

De manera análoga, \(\vec{r_2} \) se puede escribir como la diferencia entre las coordenadas \(\vec{A_2} \) y \(\vec{P} \). Usando \eqref{a2} y \eqref{Pcoo}, obtenemos

\begin{equation}
\vec{r_2}=\vec{A_2} – \vec{P}=(-2\,\text{cm}\,,\,0\,\text{cm})-(0\,\text{cm}\,,\,2.58\,\text{cm}),
\end{equation}

que es lo mismo que

\begin{equation}
\vec{r_2}=(-2\,\text{cm}\,,\,-2.58\,\text{cm}).
\end{equation}

Ahora, calculemos la magnitud del vector asociado con esta coordenada para encontrar \(r_2 \); a saber,

\begin{equation*}
r_2=|\vec{r_2}|,
\end{equation*}

\begin{equation*}
r_2=\sqrt{(-2\,\text{cm})^2+(-2.58\,\text{cm})^2},
\end{equation*}

\begin{equation}
\label{r2}
r_2\approx 3.26\,\text{cm}=0.0326\,\text{m}.
\end{equation}

De la simetría del problema \(r_3 = r_2 \), entonces

\begin{equation}
\label{r3}
r_3=0.0326\,\text{m}.
\end{equation}

Tomando los valores encontrados para las distancias de carga (\eqref{r1}, \eqref{r2} y \eqref{r3}) y la magnitud de la carga (\(q = 4 \times10^{-5}\,\text{C}\)) en la ecuación \eqref{vp2}, obtenemos

\begin{equation}
V_P=\frac{1}{4\pi (8.854\times10^{-12}\,\text{F/m})}\left(\frac{4\times10^{-5}\,\text{C}}{0.0517\,\text{m}}+\frac{-4\times10^{-5}\,\text{C}}{0.0326\,\text{m}}+\frac{-4\times10^{-5}\,\text{C}}{0.0326\,\text{m}}\right),
\end{equation}

\begin{equation}
V_P\approx -1.51\times 10^{7}\,\text{V}.
\end{equation}

b) Para calcular el trabajo necesario para llevar una carga \(Q \) desde el infinito al punto \(P \), podemos usar la relación entre el trabajo desde el punto \(A \) hasta el punto \(B \), \( W_{A \to B} \), y la energía potencial eléctrica \(U \) dada por

\begin{equation}
\label{work}
W_{A\to B}=U_{A}-U_{B},
\end{equation}

donde \(U_{A} \) y \(U_{B} \) son la energía eléctrica potencial en los puntos \(A \) y \(B \) respectivamente. La relación entre la energía potencial eléctrica de carga \(Q \) y el potencial eléctrico está dada por

\begin{equation}
\label{ui}
U_i=QV_i,
\end{equation}

donde \(i \) se usa para denotar cualquier punto en el espacio, en particular \(i = \{A, B \} \). Entonces podemos escribir la expresión del trabajo dada en la ecuación \eqref{work} usando la ecuación \eqref{ui} en ambos términos a la derecha; explícitamente,

\begin{equation}
\label{work2}
W_{A\to B}=QV_A-QV_B.
\end{equation}

Como queremos el trabajo desde el infinito hasta el punto \(P \), identificamos \(A = \infty \) y \(B = P \). Entonces podemos reescribir la ecuación \eqref{work2} como

\begin{equation}
\label{work3}
W_{\infty\to P}=QV_{\infty}-QV_P.
\end{equation}

Note de la ecuación \eqref{vpunctual} que, como \(r \to \infty \), el potencial eléctrico tiende a cero, por lo que \(V_ {\infty} = 0 \). Entonces, la ecuación \eqref{work3} se escribe como

\begin{equation}
W_{\infty\to P}=-QV_P.
\end{equation}

Tomemos el valor numérico de \(V_P \) encontrado en el inciso (a) y la magnitud de la carga dada. Entonces podemos escribir

\begin{equation}
W_{\infty\to P}=-(60\mu C)(-1.51\times 10^{7}\,\text{V}),
\end{equation}

\begin{equation}
W_{\infty\to P}\approx 906\,\text{J}.
\end{equation}

[/mepr-show]

You need to be registered and logged in to take this quiz. Log in