¡Bucle de electrones!

a) Utilice la ecuación de movimiento circular que relaciona la velocidad y el radio para despejar el período.

b) Utilice la definición de corriente que relaciona la corriente con la carga.

c) Utilice la ecuación del momento magnético. (Las dimensiones ya se conocen).

a) La velocidad del movimiento circular, en términos del período y el radio de la trayectoria, es:

\begin{equation*}
v=\frac{2\pi R}{T}.
\end{equation*}

[mepr-show rules=”4409″ unauth=”both”]

Despejando \(T \) y reemplazando valores numéricos, obtenemos:

\begin{equation*}
T\approx 9.23\times 10^{-16}\,\text{s}.
\end{equation*}

b) La corriente se puede escribir como:

\begin{equation*}
I\approx \frac{e}{T}.
\end{equation*}

que, con valores numéricos, da:

\begin{equation*}
I\approx 1.74 \times 10^{-4} \, \text{A}.
\end{equation*}

c) El momento magnético es:

\begin{equation*}
\vec{\mu}=IA\,\hat{\textbf{n}},
\end{equation*}

que se puede reescribir con dimensión para ser:

\begin{equation*}
\vec{\mu}=I \pi R \,\hat{\textbf{k}},
\end{equation*}

Insertando los valores numéricos, obtenemos:

\begin{equation*}
\vec{\mu}\approx 1.2\times 10^{-22}\,\text{A m}^2\,\hat{\textbf{k}}.
\end{equation*}

Para obtener una explicación más detallada de cualquiera de estos pasos, haga clic en “Solución detallada”.

[/mepr-show]

a) Necesitamos calcular el período orbital del electrón. Observe que a medida que el electrón se mueve en círculos, su rapidez no cambia a lo largo de la trayectoria (no hay aceleración tangencial porque la rapidez es constante). Por tanto, la única aceleración es centrípeta. En este caso, la velocidad tangencial \(v \) se puede escribir como la razón de la distancia recorrida en el tiempo. Entonces, si la distancia es el perímetro de la trayectoria circular, el tiempo será el período orbital \(T \), por lo que podemos escribir

\begin{equation}
\label{vrt}
v=\frac{2\pi R}{T},
\end{equation}

[mepr-show rules=”4409″ unauth=”both”]

donde \(R \) es el radio de la órbita. Despejando \(T \), obtenemos

\begin{equation}
T=\frac{2\pi R}{V},
\end{equation}

que numéricamente es equivalente a

\begin{equation}
T=\frac{2\pi (4.7\times 10^{-10}\,\text{m})}{3.2\times10^{6}\,\text{m/s}},
\end{equation}

\begin{equation}
T\approx 9.23\times 10^{-16}\,\text{s}.
\end{equation}

b) Considere que el electrón es un bucle de corriente. En ese caso, deberíamos usar la definición de corriente eléctrica \(I \) en términos de carga \(q \) y tiempo \(t \) como

\begin{equation}
I=\frac{dq}{dt}.
\end{equation}

En su forma aproximada (para intervalos pequeños), esto se puede escribir como

\begin{equation}
\label{current}
I\approx \frac{\Delta q}{\Delta t},
\end{equation}

donde en este caso interpretamos la corriente como la cantidad de carga \(\Delta q \) que pasa por un punto en el espacio en una cierta cantidad de tiempo \(\Delta t \). En nuestro caso, la cantidad de carga es la carga del electrón \(e \), y pasa por el mismo punto después de un intervalo de tiempo \(\Delta t = T \) (el período). Usando estos resultados en la ecuación \eqref{current}, obtenemos

\begin{equation}
I\approx \frac{e}{T}.
\end{equation}

Numéricamente, esto es

\begin{equation}
I\approx \frac{1.602\times 10^{-19}\,\text{C}}{9.23\times 10^{-16}\,\text{s}},
\end{equation}

\begin{equation}
I\approx {1.74\times 10^{-4}\,\text{A}}.
\end{equation}

c) Para calcular el momento magnético \(\vec {\mu} \) del electrón para su trayectoria circular, debemos recordar la definición de \(\vec {\mu} \):

\begin{equation}
\label{momamg}
\vec{\mu}=IA\,\hat{\textbf{n}},
\end{equation}

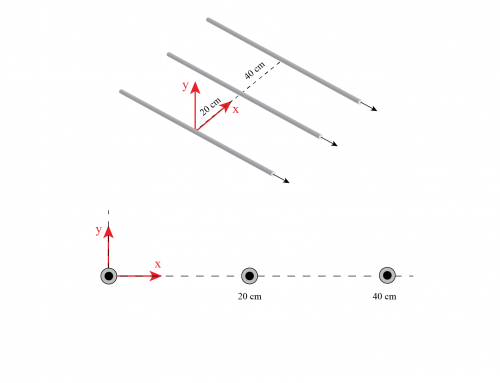
donde \(I \) es la corriente que pasa por el bucle, \(A \) es el área encerrada por el bucle y \(\hat {\textbf{n} } \) es un vector unitario normal al área \(A \) y cuya dirección viene dada por la regla de la mano derecha. Si cerramos los dedos de la mano derecha en la dirección de la corriente, el pulgar apuntará hacia arriba. Esto significa que \(\hat {\textbf{n} } \) es \(\hat {\textbf{k} } \), como se ve en la figura 1.

Figura 1: Usamos la regla de la mano derecha para encontrar la dirección del vector unitario \(\hat {\textbf{n} } \), y por tanto el vector de momento magnético \(\vec {\mu} \). Los dedos, excepto el pulgar, se cierran en la misma dirección que la corriente. El pulgar luego apunta en la dirección de \(\vec {\mu} \). A la izquierda: una vista desde arriba donde la dirección de \(\hat {\textbf{n} } \) está a lo largo del eje Z positivo. A la derecha: vista que muestra la dirección de todos los vectores implicados a lo largo de todos los ejes.

El área encerrada por el bucle es el área de un círculo de radio \(R \), es decir, \(A = \pi R^2 \). Usando esto y el hecho de que \(\hat {\textbf{n} } \) es \(\hat {\textbf{k} } \) en la ecuación \eqref{momamg}, entonces podemos escribir

\begin{equation}
\vec{\mu}=I \pi R^2 \,\hat{\textbf{k}}.
\end{equation}

Poniendo los valores numéricos para las diferentes variables, obtenemos

\begin{equation}
\vec{\mu}= (1.74\times 10^{-4}\,\text{A}) \pi (4.7\times 10^{-10}\,\text{m})^2\,\hat{\textbf{k}},
\end{equation}

\begin{equation}
\vec{\mu}\approx 1.2\times 10^{-22}\,\text{A m}^2\,\hat{\textbf{k}}.
\end{equation}

[/mepr-show]

You need to be registered and logged in to take this quiz. Log in