¡Seis bucles se mueven en un campo!

a) Utilice la definición de la fuerza electromotriz inducida (fem), donde las dimensiones de los bucles se pueden escribir en términos de la longitud horizontal, cuya derivada se puede relacionar con la velocidad dada. La diferencia para la fem de cada bucle está en las dimensiones de los bucles.

b) Utilice la definición de fem inducida para ver qué sucede esta vez.

a) La fuerza electromotriz es:

\begin{equation*}
\mathcal{E}=-\dfrac{d\Phi_B}{dt},
\end{equation*}

[mepr-show rules=”4409″ unauth=”both”]

donde el flujo magnético es exactamente \(\Phi_B = BA \) en este caso. El área es \(A = hx \). Entonces:

\begin{equation*}
\mathcal{E}= Bh \dfrac{dx}{dt},
\end{equation*}

donde \(\dfrac{dx}{dt} = v_x\). Entonces

\begin{equation*}
\mathcal{E} = Bhv_x.
\end{equation*}

Ahora para los bucles III y VI, tenemos el mismo \(h = 2L \), y entonces

\begin{equation*}
\mathcal{E}_\text{III}=\mathcal{E}_{\text{VI}}=B2Lv_x =5.88\,\text{V}.
\end{equation*}

Para el bucle IV, \(h = L \), y así obtenemos

\begin{equation*}
\mathcal{E}_{\text{IV}}=BLv_x = 2.94\,\text{V}.
\end{equation*}

Finalmente, para el bucle V, \(h = 4L \), por lo que vemos que

\begin{equation*}
\mathcal{E}_\text{V}=B4Lv_x = 11.76\,\text{V}.
\end{equation*}

La corriente es en sentido antihorario para todos los bucles.

b) Cuando los bucles están totalmente sumergidos, entonces:

\begin{equation*}
\frac{d\Phi_B}{dt}=\frac{d(-Bhw)}{dt}=0.
\end{equation*}

Entonces:

\begin{equation*}
\mathcal{E}=0,
\end{equation*}

Para obtener una explicación más detallada de cualquiera de estos pasos, haga clic en “Solución detallada”.

[/mepr-show]

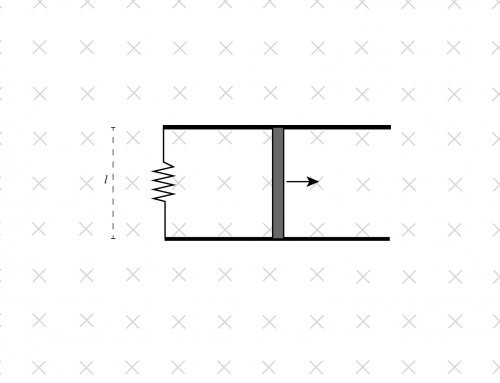
a) Nos piden que encontremos la fuerza electromotriz inducida en cada uno de los bucles a medida que ingresan al campo magnético. Para resolver este problema, primero derivaremos una expresión general para la fuerza electromotriz inducida en un bucle de altura \(h \) y ancho \(w \), como se muestra en la figura 1.

[mepr-show rules=”4409″ unauth=”both”]

En la figura 1, \(x \) es la porción horizontal del bucle que está dentro de la región con el campo magnético. A medida que el bucle se mueve hacia la derecha, \(x \) aumenta desde cero hasta su valor máximo \(w \). Para encontrar la fuerza electromotriz \(\mathcal{E} \), debemos usar la ley de inducción de Faraday, que nos dice que la tasa de cambio en el flujo magnético sobre un área dada por alguna unidad de tiempo es igual al negativo de la fuerza electromotriz;

\begin{equation}
\label{fem}
\mathcal{E}=-\dfrac{d\Phi_B}{dt},
\end{equation}

donde \(\Phi_B \) es el flujo magnético. Este flujo se define sobre una superficie \(S \) como

\begin{equation}
\label{flujomag}
\Phi_B=\int_S\vec{B}\cdot \hat{\textbf{n}}\, dA,
\end{equation}

donde \(\vec{B} \) es el campo magnético, \(\hat {\textbf{n} } \) es un vector unitario perpendicular a la superficie \(S \) en cualquier punto, y \(dA \) es un diferencial de área. En este caso, la superficie relevante es el área del bucle que está dentro del campo, por lo que el vector unitario \(\hat {\textbf{n} } \) es perpendicular al plano XY (la superficie del bucle está en el plano XY). Somos libres de elegir si \(\hat {\textbf{n} } \) se dirige hacia el eje Z positivo o hacia el eje Z negativo, lo único que importa es que sea perpendicular al plano XY. Elijamos la dirección positiva de Z.

Para una superficie plana como la del bucle y un campo magnético constante, la expresión en \eqref{flujomag} se simplifica a

\begin{equation}
\label{flujomagb}
\Phi_B=\int_S\vec{B}\cdot \hat{\textbf{n}}\, dA=\vec{B}\cdot \hat{\textbf{n}}\int_S\, dA,
\end{equation}

donde movimos el campo magnético y \(\hat {\textbf{n} } \) fuera de la integral porque ambos son constantes (sus direcciones y magnitudes no cambian). Por lo tanto, todo lo que debemos hacer ahora es integrar sobre el diferencial de área, que es lo mismo que encontrar el área total de la superficie en cuestión:

\begin{equation}
\label{fluxB}
\Phi_B=\vec{B}\cdot\hat{\textbf{n}}\, A.
\end{equation}

Aquí \(A \) es el área del bucle que intersecta el campo magnético, que podemos escribir como

\begin{equation}
\label{arealoop}
A=hx.
\end{equation}

En la figura 2, vemos que el campo magnético se dirige hacia el eje Z negativo. Entonces, podemos escribir que

\begin{equation}
\label{bexplicit}
\vec{B}=-B\,\hat{\textbf{k}},
\end{equation}

donde \(B \) es la magnitud del campo magnético. Por otro lado, sabemos que \(\hat {\textbf{n} } \) va en la dirección Z positiva (lo elegimos de esa manera), y su magnitud es uno (es un vector unitario ). Esto significa que este vector debe ser el mismo que \(\hat {\textbf{k} } \):

\begin{equation}
\label{normalvec}
\hat{\textbf{n}}=\hat{\textbf{k}}.
\end{equation}

Usando el resultado de las ecuaciones \eqref{bexplicit} y \eqref{normalvec} en la ecuación \eqref{fluxB}, obtenemos

\begin{equation}
\label{flujoB2}
\Phi_B=(-B\,\hat{\textbf{k}})\cdot\hat{\textbf{k}}\,A=-BA,
\end{equation}

donde usamos el hecho de que \(\hat{\textbf{k}}\cdot\hat{\textbf{k}}=1\). Si usamos el resultado de la ecuación \eqref{arealoop} en \eqref{flujoB2}, podemos escribir

\begin{equation}
\label{flujoB3}
\Phi_B=-Bhx.
\end{equation}

Ahora, para encontrar la fuerza electromotriz inducida, nos interesa la derivada temporal de este resultado:

\begin{equation}
\label{dtflujo}
\frac{d\Phi_B}{dt}=\frac{d(-Bhx)}{dt}.
\end{equation}

Observe que \(B \) es constante, \(h \) es constante y, por lo tanto, solo \(x \) varía (cuando el bucle entra en la región). Por tanto, podemos calcular la derivada temporal como

\begin{equation}
\label{dtflujo2}
\frac{d\Phi_B}{dt}=-Bh\frac{dx}{dt}.
\end{equation}

Pero observe ahora que la velocidad a la que \(x \) cambia con el tiempo \(dx/dt \) es igual a la rapidez del bucle a lo largo del eje X, \(v_x \). Entonces, podemos reescribir \eqref{dtflujo2} como

\begin{equation}
\label{dtflujo3}
\frac{d\Phi_B}{dt}=-Bhv_x.
\end{equation}

Usemos ahora este resultado en la ecuación \eqref{fem}, para obtener

\begin{equation}
\label{ecfem}
\mathcal{E}=-(-Bhv_x)=Bhv_x.
\end{equation}

Podemos ver que para la situación del enunciado, la fuerza electromotriz solo depende del campo magnético, la rapidez a la que el bucle entra en la región con el campo magnético y la dimensión vertical del bucle.

Ahora usaremos la ecuación \eqref{ecfem} para calcular explícitamente la fuerza electromotriz para cada bucle. Enumeraremos los bucles por fila, como se muestra en la figura 3.

Los bucles I y II tienen el mismo \(h = 3L \), por lo que tenemos

\begin{equation}
\mathcal{E}_\text{I}=\mathcal{E}_{\text{II}}=B3Lv_x.
\end{equation}

Usando los valores numéricos, obtenemos

\begin{equation}
\mathcal{E}_\text{I}=\mathcal{E}_{\text{II}}=(0.6\,\text{T})3(1.4\,\text{m})(3.5\,\text{m/s})=8.82\,\text{V},
\end{equation}

donde las unidades son voltios (V).

Ahora para los bucles III y VI, tenemos el mismo \(h = 2L \), y entonces

\begin{equation}
\mathcal{E}_\text{III}=\mathcal{E}_{\text{VI}}=B2Lv_x.
\end{equation}

Después de usar los valores numéricos, obtenemos

\begin{equation}
\mathcal{E}_\text{I}=\mathcal{E}_{\text{II}}=(0.6\,\text{T})2(1.4\,\text{m})(3.5\,\text{m/s})=5.88\,\text{V}.
\end{equation}

Para el bucle IV, \(h = L \), y así obtenemos

\begin{equation}
\mathcal{E}_{\text{IV}}=BLv_x.
\end{equation}

O, después de usar los valores numéricos, obtenemos

\begin{equation}
\mathcal{E}_\text{I}=\mathcal{E}_{\text{II}}=(0.6\,\text{T})(1.4\,\text{m})(3.5\,\text{m/s})=2.94\,\text{V}.
\end{equation}

Finalmente, para el bucle V, \(h = 4L \), por lo que vemos que

\begin{equation}
\mathcal{E}_\text{V}=B4Lv_x.
\end{equation}

O después de usar los valores numéricos, obtenemos

\begin{equation}
\mathcal{E}_\text{I}=\mathcal{E}_{\text{II}}=(0.6\,\text{T})4(1.4\,\text{m})(3.5\,\text{m/s})=11.76\,\text{V}.
\end{equation}

Observe que en todos los casos, la fuerza electromotriz inducida es positiva. Según la dirección del vector unitario \(\hat {\textbf{n} } \) y la regla de la mano derecha, esto significa que la corriente en cada bucle se mueve en sentido antihorario. Para ver por qué, todo lo que tenemos que hacer es apuntar el pulgar de la mano derecha en la dirección del vector \(\hat {\textbf{n} } \). La dirección en la que se cierran los otros dedos define la dirección positiva de la corriente. Dado que \(\mathcal{E} \) es positivo en cada caso, entonces la corriente que fluye a través de los bucles debido a la fuerza electromotriz se mueve en sentido antihorario, como se ilustra en la figura 4.

b) En el caso de que los bucles estén totalmente sumergidos en la región con el campo magnético, aún podemos calcular el flujo magnético usando la ecuación \eqref{flujoB2} . Lo único que cambia es el área \(A \) del bucle que está sumergida en la región con el campo magnético. Ahora el área es solo el área de todo el bucle, es decir

\begin{equation}
\label{areatotal}
A=hw.
\end{equation}

Luego, poniendo este resultado en la ecuación \eqref{flujoB2}, obtenemos

\begin{equation}
\Phi_B=-Bhw.
\end{equation}

Note que cada uno de estos factores es constante. Entonces, si tomamos la derivada temporal, el resultado será cero. Explícitamente,

\begin{equation}
\label{fluxb2}
\frac{d\Phi_B}{dt}=\frac{d(-Bhw)}{dt}=0.
\end{equation}

Por tanto, si volvemos a la ecuación \eqref{fem}, vemos que en este caso

\begin{equation}
\mathcal{E}=0,
\end{equation}

para todos los bucles. Esto tiene sentido; la fem siempre está asociada con cambios en el flujo magnético, pero si todo el bucle ya está dentro de la región con el campo magnético, entonces el flujo será constante porque el área del bucle es constante (y el campo no cambia).

[/mepr-show]

You need to be registered and logged in to take this quiz. Log in