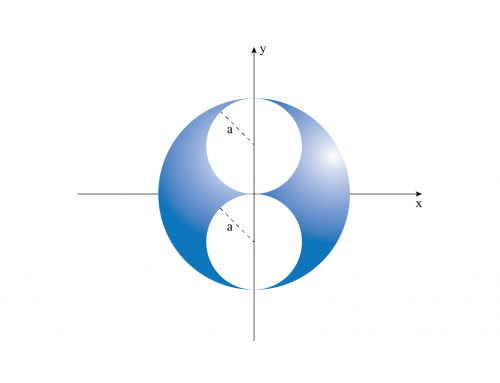
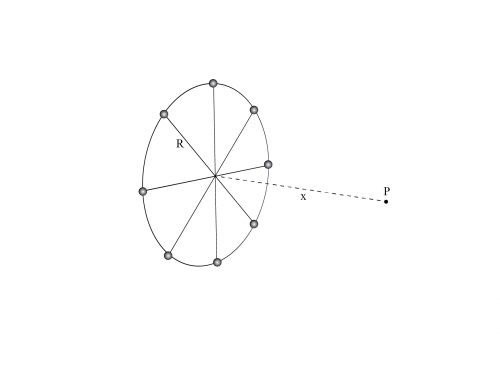
Un cable con densidad de carga uniforme \(\lambda = 75 \) mC/m se dobla para que tenga la forma que se muestra en la figura, donde \(R = 80 cm \). Calcule el potencial eléctrico en el punto \(O \).
Utilice la fórmula de potencial eléctrico para cada segmento del cable.
La fórmula del potencial eléctrico es:
\begin{equation*}
V=\frac{1}{4\pi\epsilon_0}\int\frac{dq}{r},
\end{equation*}
[mepr-show rules=”4409″ unauth=”both”]
donde la carga \(dq = \lambda dx \). Usando esta definición para cada segmento en el sistema de coordenadas en el centro del objeto obtenemos:
\begin{equation*}
V_O = \frac{1}{4\pi\epsilon_0}\int_{R}^{3R}\frac{\lambda dx}{x} + \frac{\lambda}{4\pi\epsilon_0R}\int ds + \frac{1}{4\pi\epsilon_0}\int_{R}^{3R}\frac{\lambda dx}{x},
\end{equation*}
donde las integrales son del segmento izquierdo, central y derecho, respectivamente. Al realizar las integrales obtenemos:
\begin{equation*}
V_O=\frac{\lambda\ln(3)}{4\pi\epsilon_0}+\frac{\lambda}{4\epsilon_0}+\frac{\lambda\ln(3)}{4\pi\epsilon_0},
\end{equation*}
que, después de algunas manipulaciones algebraicas y factorización, se convierte en:
\begin{equation*}
V_O=\frac{\lambda}{4\epsilon_0}\left(1+\frac{2\ln(3)}{\pi}\right).
\end{equation*}
Con valores numéricos obtenemos:
\begin{equation*}
V_O\approx 3.6\times 10^{9}\,\text{V}.
\end{equation*}
Para obtener una explicación más detallada de cualquiera de estos pasos, haga clic en “Solución detallada”.
[/mepr-show]
Para encontrar el potencial eléctrico en el punto O, usaremos el principio de superposición y dividiremos el cable en tres partes: las dos barras laterales y el segmento semicircular. El potencial eléctrico en \(O \) se puede escribir como
\begin{equation}
\label{vo}
V_O=V_L+V_C+V_R,
\end{equation}
[mepr-show rules=”4409″ unauth=”both”]
donde \(V_{L} \) y \(V_{R} \) es el potencial eléctrico producido por los segmentos rectos izquierdo y derecho y \(V_C \) es el potencial eléctrico producido por la trayectoria semicircular.
Primero calculemos \(V_L \). Para cualquier distribución de carga, el potencial eléctrico \(V \) se puede escribir como
\begin{equation}
\label{potencial}
V=\frac{1}{4\pi\epsilon_0}\int\frac{dq}{r},
\end{equation}
donde \(r \) es la distancia desde la carga \(dq \) hasta el punto donde se calcula el potencial eléctrico y \(\epsilon_0 = 8.854 \times10^{-12} \,\text{F/m} \) es una constante física conocida como permitividad del espacio libre. La carga \(dq \) es una carga diferencial ubicada en una posición arbitraria en el conductor. La integral se toma sobre todo el conductor.
Para \(V_L \), podemos identificar las variables para resolver la integral \eqref{potencial} en la figura 1.
Figura 1: Colocamos el sistema de coordenadas en el punto O. Se indica la longitud del segmento izquierdo y derecho, así como el radio de la media circunferencia. La distancia \(x \) desde el punto O hasta un diferencial de carga \(dq \) de longitud \(dx \) ubicado en el segmento izquierdo se muestra en rosa.
La distancia entre \(dq \) y el punto \(O \) es \(x \) y toma los límites superior e inferior \(3R \) y \(R \), respectivamente. Podemos usar la densidad de carga para escribir la carga infinitesimal \(dq \) en términos de una longitud infinitesimal \(dx \) como
\begin{equation}
\label{dq}
dq=\lambda dx.
\end{equation}
Poniendo todo junto en la ecuación \eqref{potencial}, podemos expresar \(V_{L} \) como la integral
\begin{equation}
\label{vl}
V_L=\frac{1}{4\pi\epsilon_0}\int_{R}^{3R}\frac{\lambda dx}{x}.
\end{equation}
Extrayendo \(\lambda \) de la integral y realizando la integral en la ecuación \eqref{vl}, obtenemos
\begin{equation}
V_{L}=\frac{\lambda}{4\pi\epsilon_0}\left(\ln|x|\right)\left.\right|_{R}^{3R},
\end{equation}
\begin{equation}
V_{L}=\frac{\lambda}{4\pi\epsilon_0}(\ln(3R)-\ln(R)),
\end{equation}
\begin{equation}
\label{vl2}
V_{L}=\frac{\lambda}{4\pi\epsilon_0}\ln\left(\frac{3R}{R}\right),
\end{equation}
donde hemos utilizado algunas propiedades del logaritmo. Simplificando el resultado de la ecuación \eqref{vl2}, obtenemos
\begin{equation}
\label{vl3}
V_{L}=\frac{\lambda\ln(3)}{4\pi\epsilon_0}.
\end{equation}
Para \(V_R \), podemos identificar las variables para resolver la integral \eqref{potencial} en la figura 2.
Figura 2: Colocamos el sistema de coordenadas en el punto O. Se indica la longitud de los segmentos izquierdo y derecho, así como el radio de la media circunferencia. La distancia \(x \) desde el punto O hasta un diferencial de carga \(dq \) de longitud \(dx \) ubicado en el segmento derecho se muestra en rosa.
La distancia entre \(dq \) y el punto \(O \) es \(x \) y toma los límites superior e inferior \(3R \) y \(R \), respectivamente. Podemos usar la ecuación de densidad de carga \eqref{dq} para escribir, de nuevo, la carga infinitesimal en términos del diferencial de longitud.
Poniendo todo junto en la ecuación \eqref{potencial}, podemos expresar \(V_{R} \) como la integral
\begin{equation}
\label{vr}
V_R=\frac{1}{4\pi\epsilon_0}\int_{R}^{3R}\frac{\lambda dx}{x},
\end{equation}
que es la misma integral que en la ecuación \eqref{vl}, entonces el resultado es el mismo, es decir
\begin{equation}
\label{vr3}
V_{R}=\frac{\lambda\ln(3)}{4\pi\epsilon_0}.
\end{equation}
Para calcular \(V_C \), notamos que la distancia desde cada punto en la trayectoria circular al punto \(O \) es solo el radio del círculo, como se ve en la figura 3.
Figura 3: Colocamos el sistema de coordenadas en el punto O. Se indica la longitud del brazo izquierdo y del brazo derecho, así como el radio de la media circunferencia. La distancia \(R \) desde el punto O hasta un diferencial de carga \(dq \) de longitud \(ds \) ubicado en la circunferencia se muestra en rosa.
Por lo tanto, podemos tomar \(r \) como una constante, a saber, \(r = R \); entonces, podemos usar la ecuación \eqref{potencial} para escribir una expresión para \(V_C \) como
\begin{equation}
\label{vc}
V_{C}=\frac{1}{4\pi\epsilon_0}\int\frac{dq}{R}.
\end{equation}
En este caso, también podemos usar la densidad de carga lineal \(\lambda \) para escribir la carga diferencial \(dq \) como
\begin{equation}
\label{dq2}
dq=\lambda ds,
\end{equation}
donde \(ds \) es el diferencial de longitud de arco. Usando el resultado de la ecuación \eqref{dq2} en la ecuación \eqref{vc}, obtenemos
\begin{equation}
\label{vc2}
V_C=\frac{1}{4\pi\epsilon_0}\int\frac{\lambda ds}{R},
\end{equation}
que, después de extraer las constantes de la integral, se convierte en
\begin{equation}
\label{vc3}
V_C=\frac{\lambda}{4\pi\epsilon_0R}\int ds.
\end{equation}
La integral de \(ds \) sobre la trayectoria semicircular da la longitud de esta trayectoria, es decir, la mitad del perímetro de un círculo de radio \(R \); por lo tanto, la ecuación \eqref{vc3} se convierte en
\begin{equation}
V_C=\frac{\lambda}{4\pi\epsilon_0R}(\pi R),
\end{equation}
que, después de un poco de simplificación, se convierte en
\begin{equation}
\label{vc4}
V_C=\frac{\lambda}{4\epsilon_0}.
\end{equation}
Poniendo los resultados de las ecuaciones \eqref{vl3} , \eqref{vr3} y \eqref{vc4} en la ecuación \eqref{vo}, obtenemos nuestro resultado
\begin{equation}
V_O=\frac{\lambda\ln(3)}{4\pi\epsilon_0}+\frac{\lambda}{4\epsilon_0}+\frac{\lambda\ln(3)}{4\pi\epsilon_0},
\end{equation}
que, después de algunas manipulaciones algebraicas y factorización, se convierte en
\begin{equation}
V_O=\frac{\lambda}{4\epsilon_0}\left(1+\frac{2\ln(3)}{\pi}\right).
\end{equation}
Usando los valores numéricos en unidades SI (\(\lambda = 0.075 \, \text{C/m} \)), terminamos con
\begin{equation}
V_O=\frac{(0.075\,\text{C/m})}{4(8.854\times10^{-12}\,\text{F/m})}\left(1+\frac{2\ln(3)}{\pi}\right),
\end{equation}
\begin{equation}
V_O\approx 3.6\times 10^{9}\,\text{V}.
\end{equation}
[/mepr-show]
You need to be registered and logged in to take this quiz. Log in

Leave A Comment