¡Tanque con conducto lateral!

a) Usando las ecuaciones cinemáticas tanto en el eje X como en el Y, encuentre el tiempo que toma caer desde la altura dada y luego encuentre la velocidad horizontal con la distancia dada.

b) Use la tasa de flujo, o ecuación de continuidad, para obtener la rapidez.

c) Use la ecuación de Bernoulli y resuelva la altura \(H\).

a) Por la posición vertical de un objeto cayendo, en este caso el agua, obtenemos:

\begin{equation*}
y_f-y_0=v_{0y}t-\frac{1}{2}gt^2,
\end{equation*}

[mepr-show rules=”4409″ unauth=”both”]

donde despejando \(t\) obtenemos:

\begin{equation*}
t = \sqrt{ \frac{2h}{g}}.
\end{equation*}

Para el desplazamiento X tenemos:

\begin{equation*}
x_f – x_i = v_{0x} t,
\end{equation*}

donde usando el tiempo \(t\) encontrado, y resolviendo para \(v_{0x} \) obtenemos:

\begin{equation*}
v_{0x}=\frac{d-x}{\sqrt{\frac{2h}{g}}},
\end{equation*}

que con valores numéricos es:

\begin{equation*}
v_{0x} \approx 4.76 \, \text{m/s}.
\end{equation*}

b) Por la ecuación de continuidad tenemos:

\begin{equation*}
v_B A_B = v_C A_C,
\end{equation*}

donde despejando \(v_B\) y con valores numéricos obtenemos:

\begin{equation*}
v_B \approx 1.90 \, \text{m/s}.
\end{equation*}

c) La ecuación de Bernoulli establece:

\begin{equation*}
P_A+\rho g z_A+\frac{1}{2}\rho v_A^2=P_C+\rho g z_C+\frac{1}{2}\rho v_C^2,
\end{equation*}

donde \(z_A = H\) y \(z_C = h\). Resolviendo para \(H\) obtenemos:

\begin{equation*}
H=h+\frac{v_C^2}{2g},
\end{equation*}

que con valores numéricos es:

\begin{equation*}
H \approx 1.86 \, \text{m}.
\end{equation*}

Para obtener una explicación más detallada de cualquiera de estos pasos, haga clic en “Solución detallada”.

[/mepr-show]

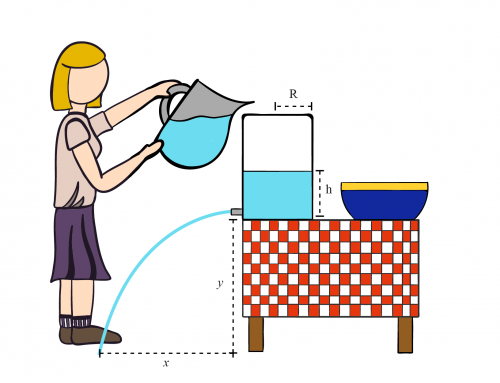
a) Nos han pedido que encontremos la rapidez a la que sale el agua de la sección más pequeña. Para resolver esta primera parte del problema, podemos utilizar la cinemática de la trayectoria parabólica del agua desde el punto en que se vierte al suelo, como se ve en la figura 1.

[mepr-show rules=”4409″ unauth=”both”]

Figura 1: Tanque lleno de agua con un agujero por donde sale el agua y describe un movimiento parabólico. Se muestran las dimensiones relevantes para el problema. Colocamos el sistema de coordenadas en el suelo justo debajo del orificio del tanque que conduce a la sección negra de la que sale el agua.

Tomando el sistema de coordenadas, como se muestra en la figura 1, podemos escribir las ecuaciones del movimiento parabólico como

\begin{equation}
\label{kinemx}
x_f\,\hat{\textbf{i}}-x_i\,\hat{\textbf{i}}=v_{0x} t \,\hat{\textbf{i}},
\end{equation}

y

\begin{equation}
\label{kinemy}
y_f\,\hat{\textbf{j}}-y_i\,\hat{\textbf{j}}=v_{0y} t \,\hat{\textbf{j}}-\frac{1}{2}gt^2 \,\hat{\textbf{j}},
\end{equation}

donde \(x_i,\, y_i\) son las coordenadas iniciales, \(x_f,\, y_f\) son las coordenadas finales y \(v_{0x} ,\,v_{0y}\) son las velocidades iniciales en los ejes X y Y respectivamente. Como de costumbre, \(g\) es la aceleración gravitacional. Centrándose solo en las magnitudes de las ecuaciones \eqref{kinemx} y \eqref{kinemy} , obtenemos (respectivamente)

\begin{equation}
\label{kinemx2}
x_f-x_i=v_{0x}t,
\end{equation}

y

\begin{equation}
\label{kinemy2}
y_f-y_0=v_{0y}t-\frac{1}{2}gt^2.
\end{equation}

Notando que cuando el agua sale, es completamente horizontal, no hay componente de la velocidad en el eje Y. Entonces \(v_y=0\), un resultado que podemos usar en \eqref{kinemy2} para simplificarlo a

\begin{equation}
y_f-y_0=-\frac{1}{2}gt^2.
\end{equation}

Desde nuestra ubicación del marco de referencia, podemos ver claramente en la tercera figura que \(x_i=x\), \(x_f=d\), \(y_i=h\) y \(y_f=0\). Reemplazando en las ecuaciones \eqref{kinemx2} y \eqref{kinemy2} , obtenemos las siguientes expresiones:

\begin{equation}
\label{kinemx3}
d-x=v_{0x}t,
\end{equation}

y

\begin{equation}
\label{kinemy3}
0-h=-\frac{1}{2}gt^2.
\end{equation}

Resolviendo para \(v_{0x}\) en la ecuación \eqref{kinemx3} , tenemos

\begin{equation}
\label{kinemx4}
v_{0x}=\frac{d-x}{t},
\end{equation}

entonces, necesitamos el tiempo \(t\) para expresar \(v_{0x}\) solo en términos de variables conocidas. Entonces podemos resolver \(t\) a partir de la ecuación \eqref{kinemy3} , obteniendo asi

\begin{equation}
t^2=\frac{2h}{g},
\end{equation}

o sacando la raíz cuadrada en ambos lados

\begin{equation}
\label{kinemy4}
t=\sqrt{\frac{2h}{g}}.
\end{equation}

Usando la expresión para el tiempo encontrada en la ecuación \eqref{kinemy4} en la ecuación \eqref{kinemx4} , obtenemos

\begin{equation}
v_{0x}=\frac{d-x}{\sqrt{\frac{2h}{g}}}.
\end{equation}

Usando los valores numéricos, encontramos que

\begin{equation}
\label{v0xvc}
v_{0x}=\frac{2.5\,\text{m}-0.7\,\text{m}}{\sqrt{\frac{2(0.7\,\text{m})}{9.8\,\text{m/s}^2}}}\approx4.76\,\text{m/s}.
\end{equation}

b) Para calcular la velocidad del agua en la sección más grande, debemos usar el principio de conservación de masa. El principio establece que la tasa a la que pasa un volumen de agua a través del área más grande debe ser la misma que la tasa a la que pasa un volumen de agua a través del área más pequeña. Esta tasa o flujo \(Q\) se puede calcular como el producto de la velocidad \(v\) y el área transversal \(A\), explícitamente:

\begin{equation}
\label{flux}
Q=vA.
\end{equation}

Entonces, el flujo en el punto B debe ser el mismo que el del punto C, es decir

\begin{equation}
\label{caudal}
Q_B=Q_C.
\end{equation}

Usando la definición de la ecuación \eqref{flux} en la ecuación \eqref{caudal}, obtenemos

\begin{equation}
\label{caudal2}
v_BA_B=v_CA_C,
\end{equation}

donde \(A_B\) y \(A_C\) son las áreas transversales en los puntos B y C respectivamente. Observe que el problema da el radio de cada sección, luego podemos usar la relación entre el área y el radio que dice \(A=\pi r^2\) para expresar los términos \(A_B\) y \(A_C\) de la ecuación \eqref{caudal2} como

\begin{equation}
v_B\pi r_B^2=v_C\pi r_C^2,
\end{equation}

donde podemos cancelar \(\pi\) para obtener una expresión más simple en términos del radio de las áreas \(r_B\) y \(r_C\) y las velocidades \(v_B\) y \(v_C\), es decir

\begin{equation}
v_B r_B^2=v_C r_C^2.
\end{equation}

Resolviendo para el único \(v_B\) desconocido que tenemos

\begin{equation}
v_B=v_C\frac{r_C^2}{r_B^2},
\end{equation}

donde \(v_C\) es la velocidad en el punto C, que es el resultado de (a) y viene dada por la ecuación \eqref{v0xvc} . Usando los valores numéricos encontramos

\begin{equation}
v_B=(4.76\,\text{m/s})\frac{(\sqrt{2}\,\text{cm})^2}{(\sqrt{5}\,\text{cm})^2}\approx 1.90\,\text{m/s}.
\end{equation}

c) Para la última parte del problema, necesitamos calcular la altura del cilindro. Para hacer esto, usaremos la ecuación de Bernoulli para la línea de corriente representada en la figura 2. Podemos usar esta ecuación porque asumimos que el flujo es estático, es decir, ninguna de las características y variables del fluido cambia con el tiempo.

Figura 2: La línea de corriente del fluido se muestra en rojo. Los parámetros de los fluidos en los puntos A, B y C, tales como la presión y la rapidez no cambian en el tiempo

Entonces podemos escribir la ecuación de Bernoulli entre los puntos A y C de la siguiente manera

\begin{equation}
\label{bernoulli}
P_A+\rho g z_A+\frac{1}{2}\rho v_A^2=P_C+\rho g z_C+\frac{1}{2}\rho v_C^2,
\end{equation}

donde \(P\) es la presión, \(z\) es la altura, \(v\) es la velocidad y \(\rho\) es la densidad del fluido. El subíndice A o C indica el punto en el que se evalúa cada variable. Observe que, dado que es un recipiente abierto, la presión en A \(P_A\) es la presión atmosférica \(P_0\). Lo mismo se aplica al punto C, ubicado justo en el agujero por donde sale el agua y la presión \(P_C\) es la presión atmosférica \(P_0\). Usando esto en la ecuación \eqref{bernoulli} , obtenemos

\begin{equation}
P_0+\rho g z_A+\frac{1}{2}\rho v_A^2=P_0+\rho g z_C+\frac{1}{2}\rho v_C^2,
\end{equation}

o cancelando \(P_0\)

\begin{equation}
\label{berni2}
\rho g z_A+\frac{1}{2}\rho v_A^2=\rho g z_C+\frac{1}{2}\rho v_C^2.
\end{equation}

De la ecuación \eqref{berni2} observe que el término \(\rho\) es común a todos los términos. Entonces podemos dividir la ecuación \eqref{berni2} en ambos lados por \(\rho\) para cancelarlo y obtener

\begin{equation}
\label{berni3}
g z_A+\frac{1}{2}v_A^2= g z_C+\frac{1}{2} v_C^2.
\end{equation}

Otra suposición que haremos es que \(H\), el nivel de agua en el recipiente, no cambia con el tiempo. Esto implica que la velocidad del agua en el punto A es aproximadamente cero, es decir \(v_A\approx0\). Usando esto en la ecuación \eqref{berni3} , se simplifica a

\begin{equation}
\label{berni4}
g z_A=g z_C+\frac{1}{2} v_C^2.
\end{equation}

Ahora, en relación con el sistema de coordenadas, como se muestra en la figura anterior, podemos ver que \(z_A=H\) y \(z_C=h\). Reemplazando estos valores en la ecuación \eqref{berni4} , obtenemos

\begin{equation}
\label{berni5}
gH=gh+\frac{1}{2}v_C^2,
\end{equation}

donde podemos resolver \(H\) dividiendo ambos lados por \(g\), entonces

\begin{equation}
\label{berni6}
H=h+\frac{v_C^2}{2g}.
\end{equation}

Usando los valores numéricos, tenemos que

\begin{equation}
H=0.7\,\text{m}+\frac{(4.76\,\text{m/s})^2}{2(9.8\,\text{m/s}^2)}\approx 1.86\,\text{m}.
\end{equation}

[/mepr-show]

You need to be registered and logged in to take this quiz. Log in