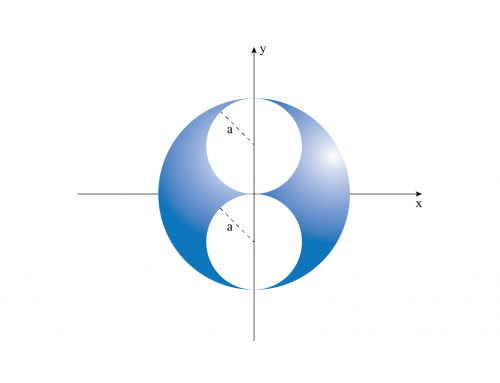
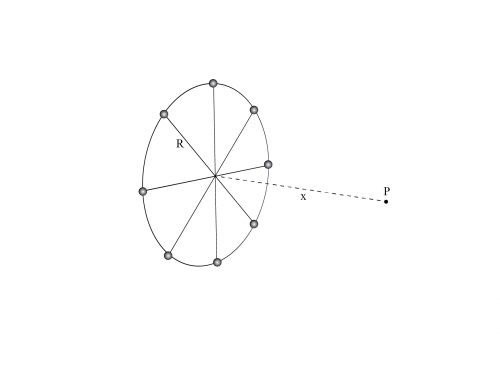
Suponga que tiene un cuarto de círculo que tiene una distribución de carga \(\lambda = \sec \theta \), como la que se muestra en la figura. Calcule el vector de campo eléctrico en el punto P.
Utilice la definición de campo eléctrico diferencial. Escriba la carga diferencial en términos de densidad lineal y escriba la distancia en términos del ángulo. Utilice estas fórmulas para integrar entre los ángulos dados.
El campo eléctrico diferencial es:
\begin{equation*}
d\vec{E}=\frac{dq}{4\pi\epsilon_0 r^2}\,\hat{\textbf{r}},
\end{equation*}
[mepr-show rules=”4409″ unauth=”both”]
donde \( \hat{\textbf{r}} = – \sin \theta \, \hat{\textbf{i}} – \cos \theta \hat{\textbf{j}}\). La carga es \(dq = \lambda ds \) y \(ds = ad \theta \). Luego, integrando en ambos lados, el campo eléctrico se puede escribir como:
\begin{equation*}
\vec{E}=\int_{-\frac{\pi}{4}}^{\frac{\pi}{4}} \frac{\sec \theta \,d\theta}{4\pi \epsilon_0 a}(-\sin(\theta)\,\hat{\textbf{i}}-\cos(\theta)\,\hat{\textbf{j}}),
\end{equation*}
donde la densidad \(\lambda = \sec \theta \) ya estaba sustituida.
Al realizar la integración, el componente \(\hat {\textbf{i} } \) es cero. Esto nos da:
\begin{equation*}
\vec{E}=-\frac{1}{8\epsilon_0 a}\,\hat{\textbf{j}}.
\end{equation*}
Para obtener una explicación más detallada de cualquiera de estos pasos, haga clic en “Solución detallada”.
[/mepr-show]
Para calcular el campo eléctrico \(\vec{E} \) producido por la distribución de carga, dividiremos la sección relevante del círculo en segmentos muy pequeños de carga \(dq \) y longitud \(ds \) (ver Figura 1 a continuación). Entonces, podemos considerar estos pequeños segmentos como cargas puntuales que producen un pequeño campo eléctrico \(d \vec{E} \), dado por la siguiente ecuación:
\begin{equation}
d\vec{E}=\frac{dq}{4\pi\epsilon_0 r^2}\,\hat{\textbf{r}},
\end{equation}
[mepr-show rules=”4409″ unauth=”both”]
donde \(r \) es la distancia desde la carga \(dq \) hasta el punto donde se calcula el campo eléctrico (P) y \(\hat {\textbf{r}} \) es el vector unitario en la dirección del vector que va de la carga \(dq \) al punto P. Como queremos el campo eléctrico para todo el segmento, necesitamos sumar todas las contribuciones de todas las cargas \(dq \). Después de hacer esto, terminamos con la ecuación integral
\begin{equation}
\label{efield1}
\int d\vec{E}=\int \frac{dq}{4\pi\epsilon_0 r^2}\,\hat{\textbf{r}}.
\end{equation}
El lado izquierdo de la ecuación \eqref{efield1} es el campo eléctrico \(\vec{E} \). Entonces,
\begin{equation}
\label{efield2}
\vec{E}=\int \frac{dq}{4\pi\epsilon_0 r^2}\,\hat{\textbf{r}}.
\end{equation}
Ahora, para continuar y poder usar esta ecuación, necesitamos expresar el vector unitario \(\hat {\textbf{r} } \) en términos de otras variables dadas por la geometría del problema. Primero, dibujemos el vector \(\vec{r} \) como se ve en la figura 1.
Figura 1: Colocamos el sistema de coordenadas en el centro de la circunferencia. El campo eléctrico \(\vec{dE} \) generado por el diferencial de carga \(dq \) de longitud \(ds \) se muestra junto con el vector de distancia \(\vec{r} \). El campo se escribe en términos de sus componentes X y Y según el ángulo \(\theta \).
En general, para todas las cargas \(dq \), el vector \(\vec{r} \) tiene una magnitud \(r \) igual al radio del semicírculo \(a \)
\begin{equation}
\label{ere}
r=a,
\end{equation}
y la dirección se dará en términos del ángulo \(\theta \), medido desde la vertical como se ve en la figura 1. Entonces, podemos escribir
\begin{equation}
\label{vecere}
\vec{r}=-a\sin(\theta)\,\hat{\textbf{i}}-a\cos(\theta)\,\hat{\textbf{j}}.
\end{equation}
El vector unitario \(\hat {\textbf{r}} \) se puede calcular como la razón de \(\vec{r} \) y \(r \). Explícitamente,
\begin{equation}
\label{runit}
\hat{\textbf{r}}=\frac{\vec{r}}{r}.
\end{equation}
Usando los resultados de las ecuaciones \eqref{ere} y \eqref{vecere} en la ecuación \eqref{runit}, obtenemos
\begin{equation}
\hat{\textbf{r}}=\frac{-a\sin(\theta)\,\hat{\textbf{i}}-a\cos(\theta)\,\hat{\textbf{j}}}{a},
\end{equation}
que se convierte en
\begin{equation}
\label{runit2}
\hat{\textbf{r}}=-\sin(\theta)\,\hat{\textbf{i}}-\cos(\theta)\,\hat{\textbf{j}}.
\end{equation}
Usando el resultado de las ecuaciones \eqref{ere} y \eqref{runit2} en la ecuación \eqref{efield2}, obtenemos
\begin{equation}
\label{efield3}
\vec{E}=\int\frac{dq}{4\pi \epsilon_0 a^2}(-\sin(\theta)\,\hat{\textbf{i}}-\cos(\theta)\,\hat{\textbf{j}}).
\end{equation}
Se nos da la distribución de densidad de carga \(\lambda \), que en términos de \(dq \) y \(ds \) se puede escribir como
\begin{equation}
\lambda=\frac{dq}{ds},
\end{equation}
de donde se puede despejar \(dq \) para obtener
\begin{equation}
\label{dq}
dq=\lambda\, ds.
\end{equation}
Ya que \(ds \) es una longitud de arco diferencial, se relaciona con el radio y un ángulo de arco diferencial \(d \theta \) de la siguiente manera
\begin{equation}
\label{ds}
ds=a\,d\theta.
\end{equation}
Usando el resultado de la ecuación \eqref{ds} en la ecuación \eqref{dq}, finalmente obtenemos una expresión para \(dq \) en términos de variables geométricas que podemos usar para integrar; a saber,
\begin{equation}
\label{dq2}
dq=\lambda a\,d\theta.
\end{equation}
Entonces podemos reemplazar \(dq \) en la ecuación \eqref{efield3} usando la expresión de la ecuación \eqref{dq2} para obtener
\begin{equation}
\label{efield4}
\vec{E}=\int_{\theta_1}^{\theta_2}\frac{\lambda a\,d\theta}{4\pi \epsilon_0 a^2}(-\sin(\theta)\,\hat{\textbf{i}}-\cos(\theta)\,\hat{\textbf{j}}),
\end{equation}
donde los límites de la integral se dan en términos de los ángulos \(\theta_1 \) y \(\theta_2 \). Extrayendo los términos constantes en la ecuación \eqref{efield4} y usando la expresión para la densidad de carga \(\lambda = \sec (\theta) \), obtenemos
\begin{equation}
\label{efield5}
\vec{E}=\frac{a}{4\pi\epsilon_0 a^2}\int_{\theta_1}^{\theta_2}d\theta\sec(\theta)(-\sin(\theta)\,\hat{\textbf{i}}-\cos(\theta)\,\hat{\textbf{j}}).
\end{equation}
Usando la identidad trigonométrica \(\sec (\theta) = \frac{1}{\cos (\theta)} \), podemos reescribir la ecuación \eqref{efield5} como
\begin{equation}
\label{efield6}
\vec{E}=\frac{1}{4\pi\epsilon_0 a}\int_{\theta_1}^{\theta_2}\frac{d\theta}{\cos(\theta)}(-\sin(\theta)\,\hat{\textbf{i}}-\cos(\theta)\,\hat{\textbf{j}}),
\end{equation}
donde también hemos cancelado la \(a \) en el numerador con una \(a \) en el denominador fuera de la integral.
Usando la ley distributiva en la ecuación \eqref{efield6}, finalmente obtenemos
\begin{equation}
\label{efield7}
\vec{E}=\frac{1}{4\pi\epsilon_0 a}\int_{\theta_1}^{\theta_2} d\theta\left(-\frac{\sin(\theta)}{\cos(\theta)}\,\hat{\textbf{i}}-\frac{\cos(\theta)}{\cos(\theta)}\,\hat{\textbf{j}}\right),
\end{equation}
que, después de un poco de simplificación, se convierte en
\begin{equation}
\label{efield8}
\vec{E}=\frac{1}{4\pi\epsilon_0 a}\int_{\theta_1}^{\theta_2} d\theta\left(-\tan(\theta)\,\hat{\textbf{i}}-1\,\hat{\textbf{j}}\right).
\end{equation}
De la figura anterior, también podemos ver que los límites son \(\theta_1 = – \pi /4 \) y \(\theta_2 = \pi /4 \), por lo que debemos resolver la integral
\begin{equation}
\label{efield9}
\vec{E}=\frac{1}{4\pi\epsilon_0 a}\int_{-\frac{\pi}{4}}^{\frac{\pi}{4}} d\theta\left(-\tan(\theta)\,\hat{\textbf{i}}-1\,\hat{\textbf{j}}\right).
\end{equation}
Que se puede dividir de la siguiente manera
\begin{equation}
\label{efield10}
\vec{E}=-\frac{1}{4\pi\epsilon_0 a}\left(\int_{-\frac{\pi}{4}}^{\frac{\pi}{4}} d\theta\tan(\theta)\,\hat{\textbf{i}}+\int_{-\frac{\pi}{4}}^{\frac{\pi}{4}} d\theta \,\hat{\textbf{j}}\right).
\end{equation}
Realizando las integrales obtenemos
\begin{equation}
\vec{E}=-\frac{1}{4\pi\epsilon_0 a}\left(\ln|\sec(\theta)|\,\hat{\textbf{i}}+\theta\,\hat{\textbf{j}}\right)\Big|_{-\frac{\pi}{4}}^{\frac{\pi}{4}},
\end{equation}
que después de evaluar se obtiene
\begin{equation}
\vec{E}=-\frac{1}{4\pi \epsilon_0 a}\left((\ln|\sec(\pi/4)|-\ln|\sec(-\pi/4)|)\,\hat{\textbf{i}}+\left(\frac{\pi}{4}-\left(-\frac{\pi}{4}\right)\right)\,\hat{\textbf{j}}\right).
\end{equation}
El componente paralelo al eje X se cancela y entonces obtenemos
\begin{equation}
\vec{E}=-\frac{1}{4\pi\epsilon_0 a}\left(0\,\hat{\textbf{i}}+\frac{\pi}{2}\,\hat{\textbf{j}}\right).
\end{equation}
La expresión final para el campo eléctrico será entonces
\begin{equation}
\vec{E}=-\frac{1}{8\epsilon_0 a}\,\hat{\textbf{j}}.
\end{equation}
[/mepr-show]
You need to be registered and logged in to take this quiz. Log in

Leave A Comment