¡Un circuito y una masa!

a) Utilice la ley de Ohm para calcular la corriente. La dirección de la corriente se puede determinar por la posición de la batería.

b) Utilice la ley de Ampere para encontrar el campo magnético inducido por el cable y encuentre la fuerza magnética. Luego, use la Segunda Ley de Newton para determinar la masa.

a) Usando la ley de Ohm y despejando \(I \), obtenemos:

\begin{equation*}
I=\frac{V}{R},
\end{equation*}

[mepr-show rules=”4409″ unauth=”both”]

que, numéricamente, es

\begin{equation*}
I\approx 16.7\,\text{A}.
\end{equation*}

b) La Ley de Ampere establece:

\begin{equation*}
\oint \vec{B} \cdot d \vec{r} = \mu_0 I_c.
\end{equation*}

El lado derecho de la ecuación se convierte en \(B 2 \pi r \). La corriente encerrada es \(I \). Entonces, despejando \(B \) obtenemos:

\begin{equation*}
B = \frac{\mu_0 I}{2 \pi r}.
\end{equation*}

La fuerza magnética es:

\begin{equation*}
{F}= \frac{\mu_0 I I’}{2\pi x}.
\end{equation*}

Usando la Segunda Ley de Newton en el cable, obtenemos:

\begin{equation*}
F – mg = 0,
\end{equation*}

donde, reemplazando la fuerza magnética encontrada recientemente y despejando \(m \), obtenemos:

\begin{equation*}
m=\frac{L\mu_0 I I’}{2\pi x g}.
\end{equation*}

Al introducir valores numéricos se obtiene:

\begin{equation*}
m \approx 0.6 \, \text{g}.
\end{equation*}

Para obtener una explicación más detallada de cualquiera de estos pasos, haga clic en “Solución detallada”.

[/mepr-show]

a) Para la primera parte, se nos pide encontrar la dirección de la corriente en el circuito y su valor entre los puntos \(a \) y \(b \). Comencemos usando la ley de Ohm para encontrar la magnitud de la corriente \(I \), es decir

\begin{equation}
\label{ohm}
V=IR,
\end{equation}

[mepr-show rules=”4409″ unauth=”both”]

donde \(V \) es el voltaje en la batería y \(R \) el valor de la resistencia. Despejando \(I \) en la ecuación \eqref{ohm}, obtenemos

\begin{equation}
I=\frac{V}{R},
\end{equation}

que numéricamente es

\begin{equation}
I=\frac{200\,\text{V}}{12\,\Omega},
\end{equation}

\begin{equation}
I\approx 16.7\,\text{A}.
\end{equation}

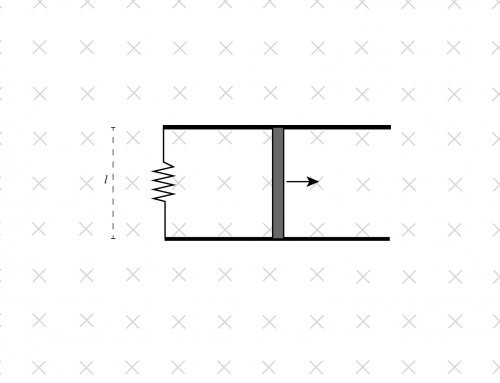
La dirección de la corriente se muestra en la figura 1, donde la corriente fluye desde el terminal positivo de la batería al terminal negativo. Por lo tanto, va de \(b \) a \(a \).

Figura 1: Dirección de la corriente \(I \) a través del circuito. El segmento \(a-b \) está separado una distancia \(x \) del cable de longitud \(l \) y masa \(m \).

b) Consideremos ahora una corriente de 20 A que fluye por el cable delgado y una masa desconocida \(m \) que cuelga de él. Primero necesitamos calcular la dirección en la que debe fluir la corriente para que la masa permanezca en equilibrio. Debido a que la longitud de ambos cables (el segmento \(ab \) y el cable delgado) es mucho mayor que la distancia que los separa, podemos considerarlos como infinitos y paralelos a los efectos del cálculo. El siguiente paso es encontrar la fuerza magnética que produce un alambre infinito a cierta distancia \(r \) sobre otro alambre. Se puede encontrar esta fuerza en dos subpasos: (i) primero encontramos el campo magnético producido por un cable a cierta distancia \(r \), y (ii) luego usamos la fuerza de Lorentz para encontrar la fuerza que siente otro cable debido al campo magnético que se encuentra en (i) (si el lector ya conoce la fuerza que siente un cable debido a un cable diferente, entonces el lector puede saltarse los siguientes dos párrafos, pero aquí queremos derivar el resultado de algunos principios básicos).

Encontrar el campo magnético producido por un cable:

Entonces, consideremos primero un cable largo y recto que lleva una corriente \(i \). Primero, usaremos el hecho de que las líneas del campo magnético siempre van en círculos alrededor de un cable recto, y la dirección de éstas se puede obtener de la regla de la mano derecha. En particular, apunte el pulgar de su mano derecha en la dirección de la corriente y luego rodee el cable con los otros dedos. La forma en que se envuelven los dedos determina la dirección del campo alrededor del cable, como en la figura 2.

Figura 2: A la izquierda: líneas de campo magnético \(\vec{B} \) producidas por un cable con corriente \(\vec{I} \). Observe que usamos la regla de la mano derecha para encontrar la dirección del campo magnético. Si coloca el pulgar de su mano derecha en la dirección de la corriente y envuelve el cable con los otros dedos, entonces la dirección a la que apuntan los otros dedos indica si el campo magnético es en sentido horario o antihorario. A la derecha: Una vista desde arriba, con la corriente fluyendo fuera de la pantalla. Observe que el campo magnético va en sentido antihorario.

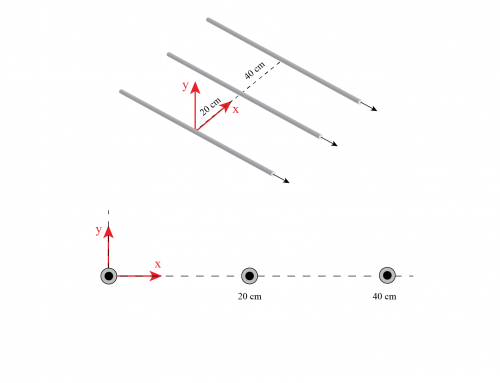
Observe en la figura 2 que cada círculo de radio \(r \) tiene líneas de campo magnético de magnitud constante, siempre apuntando en la dirección tangencial (siempre apuntando en sentido antihorario). Si hacemos el mismo razonamiento pero para el problema en cuestión, obtendremos lo siguiente (ver figura 3).

Figura 3: A la izquierda: dirección del campo magnético \(\vec{B} \) generado por la corriente que fluye a través del segmento \(ab \). Encontramos la dirección usando la regla de la mano derecha, donde el pulgar apunta en la dirección de la corriente y los otros dedos indican la dirección del campo (en sentido antihorario o en el sentido de las agujas del reloj alrededor del cable). Los puntos indican que el campo magnético que sale de la pantalla, mientras que las cruces representan que el campo magnético que entra en la pantalla. A la derecha: use la regla de la mano derecha para encontrar la dirección de circulación del campo magnético. También se muestra la corriente \(I’\) que pasa a través del cable ligero \(I’ \).

Ahora, la regla de la mano derecha nos dio la dirección, pero para encontrar la magnitud del campo producido por el cable, usaremos la Ley de Ampère, que establece que

\begin{equation}
\label{eqref:ampere1}
\oint \vec{B} \cdot d \vec{r} = \mu_0 I_c.
\end{equation}

Esta integral es una integral de camino junto con un camino cerrado P (que somos libres de elegir) que encierra una corriente \(I_c \) . Aquí, \(d \vec{r} \) es un elemento diferencial de longitud que apunta a lo largo del camino de integración, y \(\mu_0 \) es la constante de permeabilidad (también conocida como la ‘constante magnética’). Por lo tanto, podemos usar esta ecuación para encontrar el campo magnético producido por el segmento \(ab \) con la corriente \(I \)

En este caso, podemos realizar fácilmente la integración debido a la simetría del campo magnético, que siempre va en círculos, como se explicó anteriormente. Para realizar la integración, primero debemos elegir un camino. Claramente, queremos un camino tal que \(\vec{B} \cdot d \vec{r} \) (el término a integrar) sea lo más simple posible. Entonces, en nuestro caso, elegimos como camino de integración un un círculo de radio \(r \) alrededor del cable. Como podemos ver en la figura 4, este camino es conveniente porque el campo \(\vec{B} \) y el diferencial de camino \(d \vec{r} \) son siempre paralelos entre sí:

Figura 4: Para aplicar la Ley de Ampère, elegimos como camino un círculo que encierra el cable (la corriente) en su punto medio. Observe que estae camino garantiza que el vector del campo magnético sea siempre (en cualquier punto del círculo) paralelo al diferencial de línea \(d \vec{r}\) (dado que son paralelos, y dado que el campo magnético tiene la misma magnitud en todo el círculo, entonces el producto \(\vec{B} \cdot d \vec{r} = B dr \) es una constante que se puede escribir como \(Bdr \)).

Así, la Ley de Ampère se convierte en

\begin{equation}
\label{eqref:ampere2}
\oint \vec{B} \cdot d \vec{r} = \oint B dr = B \oint dr = \mu_0 I,
\end{equation}

donde usamos el hecho de que \(I_c = I \), dado que la corriente encerrada por este círculo es \(I \), y donde también sacamos \(B \) de la integración porque es constante en cualquier punto alrededor del círculo. Finalmente, todo lo que necesitamos calcular es \(\oint dr \), que es la integral de camino del diferencial de línea a lo largo del círculo. En otras palabras, esta integración corresponde a la longitud total del camino en cuestión, que es solo el perímetro del círculo. Por lo tanto

\begin{equation}
\label{eqref:ampere2b}
B \oint dr = 2 \pi r = \mu_0 I
\end{equation}

Por lo tanto,

\begin{equation}
\label{eqref:ampere 3}
B 2 \pi r = \mu_0 I,
\end{equation}

y despejando B, obtenemos

\begin{equation}
\label{wirefield}
B = \frac{\mu_0 I}{2 \pi r}.
\end{equation}

Entonces, hemos encontrado la magnitud del campo magnético del cable a una distancia \(r \) (y ya encontramos la dirección).

Fuerza magnética sentida por un alambre

Pasamos al subpaso dos, donde encontraremos la fuerza magnética que siente el otro cable debido al campo magnético producido por el primer cable, que acabamos de calcular. Esta fuerza viene dada simplemente por la ley de fuerza de Lorentz en ausencia de un campo eléctrico, y que establece que la fuerza que siente una carga \(q \) que se mueve con velocidad \(vec{v} \) en presencia de un campo magnético es

\begin{equation}
\label{florentz}
{\vec{F}}=q\vec{v}\times \vec{B}.
\end{equation}

En el caso presente, queremos encontrar la fuerza que siente la corriente \(I ‘\) en el cable inferior. Pero recuerde que la corriente es solo carga en el tiempo, y entonces \(I ‘= q/t \), de donde se sigue que \(I’t = q \). Usamos esto en la ecuación anterior para obtener

\begin{equation}
\label{florentz2}
{\vec{F}}=I’t\vec{v}\times \vec{B}.
\end{equation}

Y ahora usemos que la velocidad es el desplazamiento en el tiempo, es decir,

\begin{equation}
\label{velocity}
\vec{v}=\frac{\vec{L}}{t},
\end{equation}

donde \(\vec{L} \) es un vector que apunta en la dirección de la corriente sobre el cable inferior, y cuya magnitud es \(l \) (la longitud del segmento). Si usamos este resultado en la ecuación \eqref{florentz2}, obtenemos

\begin{equation}
\label{florentz3}
{\vec{F}}=I’t\frac{\vec{L}}{t}\times \vec{B}.
\end{equation}

El tiempo se cancela y obtenemos

\begin{equation}
\label{florentz4}
{\vec{F}}=I'{\vec{L}}\times \vec{B}.
\end{equation}

Ahora, antes de continuar, encontremos la magnitud de esta fuerza. Usando la definición de la magnitud del producto cruz, tenemos

\begin{equation}
\label{florentz5}
{F}=I’LB \sin \theta,
\end{equation}

donde \(\theta \) es el ángulo entre los vectores. Observe que \(\vec{L} \) va horizontalmente hacia la izquierda o hacia la derecha (depende de si la corriente \(I ‘\) va hacia la izquierda o hacia la derecha). Y como explicamos antes, \(\vec{B} \) (el campo producido por el cable superior) sale de la pantalla en la región donde se coloca el cable inferior. Por lo tanto, \(\vec{B} \) y \(\vec{L} \) siempre serán perpendiculares, lo que significa que el ángulo entre ellos es \(90^{\circ} \). Y entonces la ecuación anterior se convierte en

\begin{equation}
\label{florentz6}
{F}=I’LB.
\end{equation}

Antes reemplazamos aquí la magnitud del campo magnético encontrado con la ecuación \eqref{wirefield}, pensemos en la dirección de esta fuerza (ya sabemos que debe ser perpendicular a los vectores \(\vec{L}\) y \(\vec{B}\) porque la fuerza proviene del producto cruz entre estos vectores, pero todavía hay dos opciones abiertas; o la fuerza va hacia arriba o hacia abajo, en ambos casos sería perpendicular). Simplemente podemos usar la regla de la mano derecha para determinar la dirección:

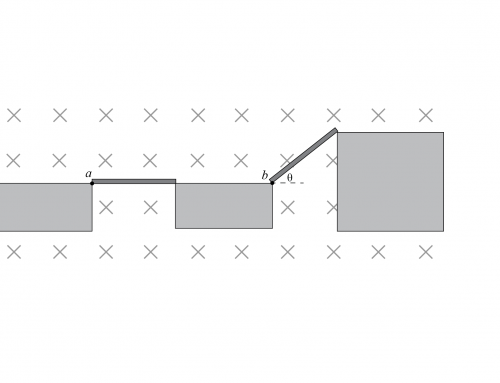
Figura 5: Izquierda: Dirección de la fuerza \(\vec{F} \) ejercida por el campo magnético generado por el segmento \(a-b \) en el cable. Nuevamente, la dirección de la fuerza se encuentra usando la regla de la mano derecha. Observe que si ambas corrientes apuntan en la misma dirección, la fuerza aumenta, lo que significa que los cables se atraen. Derecha: Vista transversal de los dos cables y el campo magnético generado por el segmento \(ab \). La fuerza es atractiva entre ambos cables.

A partir del diagrama, está claro que si las corrientes son paralelas, entonces el cable inferior se siente atraído por el cable superior, que es lo que necesitamos si queremos que el cable inferior mantenga la masa en equilibrio. El lector puede notar fácilmente que si las corrientes fueran antiparalelas, los cables se repelerían entre sí (use nuevamente la regla de la mano derecha, pero con la dirección opuesta para la corriente \(I ‘\)).

Finalmente, usamos el campo magnético encontrado con la ecuación \eqref{wirefield} de vuelta en la ecuación \eqref{florentz6} para obtener

\begin{equation}
\label{fmag}
{F}=I’L\frac{\mu_0 I I’}{2\pi x}=\frac{\mu_0 I I’}{2\pi x}
\end{equation}

Las fuerzas ejercidas sobre el cable ligero son entonces el peso de la masa \(m \) y la fuerza \(F \) (que dibujamos hacia arriba) requeridas para que el cable ligero permanezca en equilibrio. Como explicamos anteriormente, necesitamos que las corrientes sean paralelas (apunten en la misma dirección) para que la fuerza \(F \) sea una fuerza de atracción entre el cable ligero y el cable del segmento \(ab \). Haciendo un diagrama de cuerpo libre sobre el cable inferior, obtenemos lo que se muestra en la figura 6.

Figura 6: Diagrama de cuerpo libre del cable de luz con la fuerza magnética \(\vec{F} \) hacia arriba y el peso \(\vec{W} = -mg \, \hat {\textbf{j} } \) hacia abajo. Observe el sistema de coordenadas utilizado.

Ahora podemos escribir la segunda ley de Newton:

\begin{equation}
\label{newton2}
\sum \vec{F}=m\vec{a}.
\end{equation}

Pero en equilibrio, no hay aceleración y así obtenemos

\begin{equation}
\label{newton3}
\sum \vec{F}=\vec{0}.
\end{equation}

En este caso \(\sum \vec{F} \) es el peso de la masa \(m \) dirigido hacia abajo, más la fuerza \(F \) dirigida hacia arriba. Ignoramos la masa del cable ligero ya que supondremos que es mucho menor que \(m \). De la ecuación \eqref{newton3}, obtenemos

\begin{equation}
-mg\,\hat{\textbf{j}}+F\,\hat{\textbf{j}}=\vec{0}.
\end{equation}

Centrándonos solo en la magnitud, esto se convierte en

\begin{equation}
\label{newton4}
-mg+F=0,
\end{equation}

donde \(g \) es la aceleración gravitacional de la Tierra. Despejando \(m \), obtenemos

\begin{equation}
m=\frac{F}{g}.
\end{equation}

Usando la expresión para \(F \) dada en la ecuación \eqref{fmag}, finalmente obtenemos

\begin{equation}
m=\frac{L\mu_0 I I’}{2\pi x g}.
\end{equation}

Usando los valores numéricos en las unidades SI, de modo que \(L=0.3\,\text{m}\) y \(x=3.4\times10^{-3}\,\text{m}\), obtenemos

\begin{equation}
m=\frac{(0.3\,\text{m})(4\pi\times 10^{-7}\,\text{T m A}^{-1})(16.7\,\text{A})(20\,\text{A})}{2\pi (3.4\times 10^{-3}\,\text{m})(9.81\,\text{m/s}^2)},
\end{equation}

\begin{equation}
m\approx 6\times 10^{-4}\,\text{kg}=0.6\,\text{g}.
\end{equation}

[/mepr-show]

You need to be registered and logged in to take this quiz. Log in