¡Diana!

a) No se conoce la cantidad de tiempo que el dardo estaba volando! Trate de encontrar el tiempo a partir de la ecuación de movimiento a lo largo de X y reemplácelo en la ecuación de movimiento a lo largo de Y.

b) En el numeral anterior, se obtuvo una ecuación en función del ángulo, las posiciones y la rapidez inicial. Entonces, use la misma ecuación, pero esta vez intente encontrar \( \theta \). ¡Tiene que usar la ecuación cuadrática!

a) Para un objeto con velocidad constante, la ecuación de movimiento es:

\begin{equation*}
\vec{x}_f=\vec{x}_{i}+\vec{v}_{ix}t,
\end{equation*}

donde \(v = v_i \cos \theta \). Luego, despejando \(t\):

\begin{equation*}
t=\frac{x_f-x_i}{v_i\cos(\theta)}.
\end{equation*}

La ecuación de movimiento a lo largo de Y es:

\begin{equation*}
y_f=y_i+v_{iy}t-\frac{1}{2}gt^2,
\end{equation*}

donde \(v = v_i \sin \theta \). Ahora, tomando \( x_i = y_i = 0 \) y usando la variable de tiempo \( t \) encontrada antes y después de usar algo de álgebra, la ecuación anterior se simplifica a:

\begin{equation*}
y_f=x_f\tan(\theta)-\frac{gx_f^2\sec^2(\theta)}{2v_i^2}.
\end{equation*}

Despejando \( v_i \), obtenemos:

\begin{equation*}
v_i=17.5\,\text{m/s}.
\end{equation*}

b) Considerando \( y_f = 0 \), podemos usar la siguiente ecuación que obtuvimos antes:

\begin{equation*}
0=x_f\tan(\theta)-\frac{gx_f^2\sec^2(\theta)}{2v_i^2},
\end{equation*}

donde ahora la variable \(\theta\) es la variable desconocida. Si reorganizamos los términos, podemos identificar las constantes \(a,b,c\) de la ecuación cuadrática:

\begin{equation*}
\left(-\frac{gx_f^2}{2v_i^2}\right)\tan^2(\theta)+x_f\tan(\theta)+\left(-\frac{gx_f^2}{2v_i^2}\right)=0.
\end{equation*}

Despejando \( \tan \theta \), y después de tomar el arco-tangente para ambas respuestas, obtenemos el resultado final, a saber,

\begin{equation*}
\theta=\arctan(0.023)\approx 1.33^{\circ},
\end{equation*}

y

\begin{equation*}
\theta=\arctan(1.405)\approx 54.56^{\circ}.
\end{equation*}

Ambas trayectorias golpean el centro del tablero. Ambas respuestas son correctas, y ambas son realistas porque es fácil lanzar el dardo casi horizontalmente, ¡y también fácil de lanzar en un ángulo de 54 grados!

Para obtener una explicación más detallada de cualquiera de estos pasos, haga clic en “Solución detallada”.

(a) Necesitamos calcular la rapidez inicial del dardo. Para resolver ambas partes de este problema, tenemos que escribir las ecuaciones para el movimiento parabólico. Recuerde que en este tipo de movimiento, el objeto tiene una aceleración gravitacional constante a lo largo de Y y una velocidad constante a lo largo de X.

Para un objeto con velocidad constante, la ecuación de movimiento es

\begin{equation}
\vec{x}_f=\vec{x}_{i}+\vec{v}_{ix}t,
\end{equation}

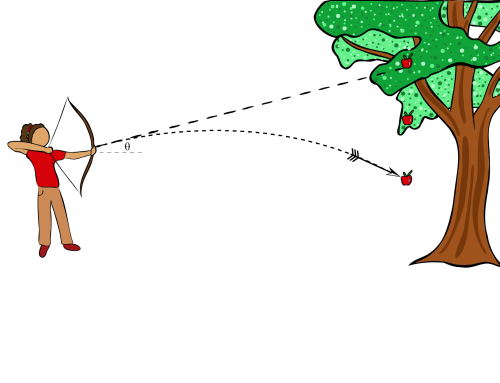
donde \( \vec{v} _{ix} \) es la velocidad largo de X, \( t \) el tiempo, \( \vec{x} _f \) la posición final, y \( \vec{x} _{i} \) la posición inicial. También ayudará a facilitar las cosas si asumimos que el lanzamiento no es horizontal en la parte a) y si esperamos hasta el final de los cálculos para poner a cero el ángulo del lanzamiento (que es la condición para un lanzamiento horizontal). Esto es útil porque nos ayudará a derivar un resultado que también podemos usar para la parte b). Entonces, escojamos un sistema de coordenadas conveniente y supongamos que el tiro marca un ángulo dado \( \theta \) con X, como se ilustra en la figura 1.

Figura 1: Colocamos el sistema de coordenadas en la posición inicial del dardo, que está a la misma altura que el centro del tablero (como indica la línea discontinua). Suponemos que el tiro marca un ángulo dado con X, pero para la parte a) podemos simplemente establecer este ángulo en cero.

Según este sistema, la velocidad largo de X es positiva y obtenemos

\begin{equation}
x_f\,\hat{\textbf{i}}=x_i\,\hat{\textbf{i}}+v_{ix}t\,\hat{\textbf{i}}.
\end{equation}

Ahora, de la figura anterior, está claro que \(v_{ix}=v_i \cos \theta \). Por lo tanto, obtenemos

\begin{equation}
x_f\,\hat{\textbf{i}}=x_i\,\hat{\textbf{i}}+v_{i}\cos (\theta) t\,\hat{\textbf{i}}.
\end{equation}

Centrándonos solo en las magnitudes, esto da

\begin{equation}
\label{kinemx}
x_f=x_i+v_i (\cos \theta) t.
\end{equation}

Para encontrar la rapidez inicial a partir de esta ecuación, aún necesitamos encontrar el tiempo, por lo que necesitamos más ecuaciones. Así que consideremos lo que está sucediendo a lo largo de Y.

En Y, el dardo tiene una aceleración gravitacional constante, que es negativa según el sistema. En la parte b), no hay rapidez vertical inicial (el dardo se lanza horizontalmente), pero como dijimos anteriormente, asumiremos el caso general donde hay cierta rapidez inicial a lo largo de Y y solo al final de nuestros cálculos utilizaremos el hecho de que esta rapidez es cero. También observe que la posición inicial es positiva según el sistema. Por lo tanto, la ecuación de movimiento a lo largo de Y es

\begin{equation}
y_f\,\hat{\textbf{j}}=y_i\,\hat{\textbf{j}}+v_i\sin(\theta)t\,\hat{\textbf{j}}-\frac{1}{2}gt^2\,\hat{\textbf{j}}.
\end{equation}

Centrándonos solo en las magnitudes, obtenemos

\begin{equation}
\label{kinemy}
y_f=y_i+v_i\sin(\theta)t-\frac{1}{2}gt^2,
\end{equation}

donde \(y_i\) y \(y_f\) son las posiciones inicial y final a lo largo del eje Y respectivamente. Entonces, tenemos dos ecuaciones que involucran el tiempo. Despejando el tiempo \(t\) en la ecuación \eqref{kinemx}, obtenemos

\begin{equation}
v_i\cos(\theta) t=x_f-x_i,
\end{equation}

que es lo mismo que

\begin{equation}
t=\frac{x_f-x_i}{v_i\cos(\theta)}.
\end{equation}

Usando esta expresión para el tiempo en la ecuación \eqref{kinemy} , obtenemos

\begin{equation}
y_f=y_i+v_i\sin(\theta)\left(\frac{x_f-x_i}{v_i\cos(\theta)}\right)-\frac{1}{2}g\left(\frac{x_f-x_i}{v_i\cos(\theta)}\right)^2.
\end{equation}

Esto simplifica a

\begin{equation}
\label{traj}
y_f=y_i+(x_f-x_i)\tan(\theta)-\frac{1}{2}g\frac{(x_f-x_i)^2\sec^2(\theta)}{v_i^2},
\end{equation}

donde hemos usado las identidades trigonométricas \(\sin(\theta)/\cos(\theta)=\tan(\theta)\) y \(1/\cos^2(\theta)=\sec^2(\theta)\).

Ahora, puesto que colocamos el origen de nuestro sistema de coordenadas en la mano de Min cuando lanza el dardo, \( x_i = y_i = 0 \), y por lo tanto la ecuación \eqref{traj} se simplifica a

\begin{equation}
\label{trajectory}
y_f=x_f\tan(\theta)-\frac{gx_f^2\sec^2(\theta)}{2v_i^2}.
\end{equation}

Podemos usar esta ecuación para resolver la rapidez inicial del dardo \(v_i\). Para el primer lanzamiento, el dardo va horizontalmente, por lo que el ángulo inicial es cero, como se muestra en la figura 2.

Figura 2: Sistema de coordenadas para los dardos.

Por tanto, \eqref{trajectory} se convierte en

\begin{equation}
y_f=x_f\tan(0^{\circ})-\frac{gx_f^2\sec^2(0^{\circ})}{2v_i^2},
\end{equation}

o, de manera equivalente,

\begin{equation}
\label{above1}
y_f=-\frac{gx_f^2}{2v_i^2}.
\end{equation}

Sabemos que en el primer lanzamiento, el dardo recorre una distancia a lo largo del eje X de \( x_f = 2.5 \, \text{cm} \) y aterriza en \( y_f = -10 \, \text{cm} = -0.10 \, \text{m} \), que es negativo porque está por debajo de nuestro sistema de coordenadas. Entonces, tenemos todo lo que necesitamos para despejar \( v_i \) en la ecuación \eqref{above1} .

Primero, dividimos por \( y_f \) en ambos lados y multiplicamos por \( v_i ^ 2 \), para obtener

\begin{equation}
v_i^2=-\frac{gx_f^2}{2y_f}.
\end{equation}

Después de sacar la raíz cuadrada en ambos lados y usar la raíz positiva (ya que \( v_i \) es la magnitud de la velocidad, entonces siempre es positiva), obtenemos

\begin{equation}
v_i=\sqrt{-\frac{gx_f^2}{2y_f}}.
\end{equation}

Usando los valores numéricos, obtenemos

\begin{equation}
v_i=\sqrt{-\frac{(9.8\,\text{m/s}^2)(2.5\,\text{m})^2}{2(-0.10\,\text{m})}},
\end{equation}

que es igual a

\begin{equation}
v_i=17.5\,\text{m/s}.
\end{equation}

(b) Para calcular el ángulo del segundo tiro, debemos volver a la ecuación \eqref{trajectory} y tomar \( y_f = 0 \) porque el centro del tablero es el mismo que la altura inicial, que, según nuestro sistema de coordenadas, es cero. Entonces podemos escribir

\begin{equation}
0=x_f\tan(\theta)-\frac{gx_f^2\sec^2 (\theta)}{2v_i^2}.
\end{equation}

Usando la identidad trigonométrica \(\sec^2{\theta}=1+\tan^2(\theta)\) en esta ecuación, obtenemos

\begin{equation}
0=x_f\tan(\theta)-\frac{gx_f^2(1+\tan^2(\theta))}{2v_i^2},
\end{equation}

donde ahora tenemos una ecuación cuadrática para \( \tan ( \theta) \). Reorganicemos algunos términos en la ecuación anterior para que podamos ver esta ecuación cuadrática con mayor claridad. Expandamos el término entre paréntesis para obtener

\begin{equation}
x_f\tan(\theta)-\frac{gx_f^2}{2v_i^2}-\frac{gx_f^2}{2v_i^2}\tan^2(\theta)=0.
\end{equation}

Si reorganizamos los términos e identificamos las constantes \(a,b,c\) de la ecuación cuadrática, obtenemos

\begin{equation}
\left(-\frac{gx_f^2}{2v_i^2}\right)\tan^2(\theta)+x_f\tan(\theta)+\left(-\frac{gx_f^2}{2v_i^2}\right)=0,
\end{equation}

o equivalente,

\begin{equation}
a\tan^2(\theta)+b\tan(\theta)+c=0.
\end{equation}

Las soluciones de esta ecuación cuadrática son

\begin{equation}
\tan(\theta)=\frac{-b\pm\sqrt{b^2-4ac}}{2a}.
\end{equation}

Después de usar las expresiones explícitas para \(a,b\) y \(c\), esto se convierte en

\begin{equation}
\tan(\theta)=\frac{-x_f\pm\sqrt{x_f^2-4\left(\frac{gx_f^2}{2v_i^2}\right)^2}}{2\left(-\frac{gx_f^2}{2v_i^2}\right)}.
\end{equation}

Ingresemos los valores numéricos para obtener

\begin{equation}
\tan(\theta)=\frac{-(2.5\,\text{m})\pm\sqrt{(2.5\,\text{m})^2-4\left(\frac{(9.8\,\text{m/s}^2)(2.5\,\text{m})^2}{2(17.5\,\text{m/s})^2}\right)}}{2\left(-\frac{(9.8\,\text{m/s}^2)(2.5\,\text{m})^2}{2(17.5\,\text{m/s})^2}\right)}.
\end{equation}

Esto nos da dos soluciones:

\begin{equation}
\tan(\theta)\approx 0.023
\end{equation}

y

\begin{equation}
\tan(\theta)\approx 1.405.
\end{equation}

Después de tomar el arco-tangente para ambas respuestas, obtenemos nuestro resultado final, a saber,

\begin{equation}
\theta=\arctan(0.023)\approx 1.33^{\circ},
\end{equation}

y

\begin{equation}
\theta=\arctan(1.405)\approx 54.56^{\circ}.
\end{equation}

Figura 3: Las líneas punteadas representan dos trayectorias posibles para el dardo, de modo que golpee el centro del tablero. Ambas trayectorias tienen la misma rapidez inicial pero diferentes ángulos con respecto al eje X.

En la figura 3, podemos ver que ambas trayectorias golpean el centro del tablero. Ambas respuestas son correctas y ambas realistas porque es fácil lanzar el dardo casi horizontalmente y en un ángulo de 54 grados.

You need to be registered and logged in to take this quiz. Log in