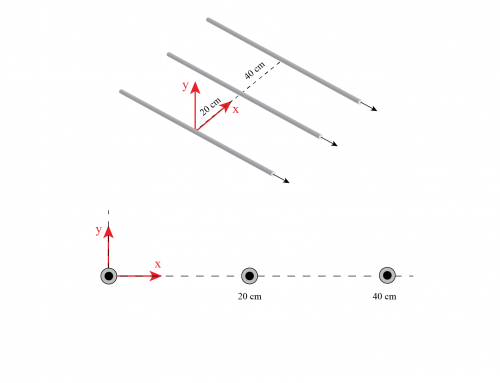
En el tiempo \(t = 0 \), un protón tiene velocidad \(\vec{v} = 1.8 \times 10^5 \, \text{m/s} \, \hat{\textbf{i}} + 2.4 \times 10^5 \, \text{m/s} \, \hat{\textbf{j}} \) y entra en una región de campo magnético \(\vec{B} = 0.6 \, \text{T} \, \hat{\textbf{i}}\). Ignorando los efectos de la gravedad, calcule en \(t = 0 \):
(a) La fuerza sobre el protón.
(b) La aceleración del protón.
(c) El radio de la trayectoria helicoidal resultante.
(d) La rapidez angular del protón.
(e) La distancia recorrida a lo largo del eje perpendicular al plano helicoidal después de cada revolución.
a) La definición de fuerza magnética se puede utilizar para encontrar la respuesta.
b) Utilice la segunda ley de Newton para encontrar la aceleración.
c) Utilice una ecuación de movimiento circular para relacionar el radio con la aceleración centrípeta.
d) La velocidad y el radio son variables conocidas, por lo que la velocidad angular se puede obtener fácilmente.
e) Encuentre el tiempo necesario para hacer una revolución completa. Usando un componente de la velocidad, se puede encontrar la distancia.
a) La fuerza magnética es:
\begin{equation*}
\vec{F}=q\vec{v}\times\vec{B}.
\end{equation*}
[mepr-show rules=”4409″ unauth=”both”]
Reemplazando los valores numéricos y realizando el producto cruzado con los vectores unitarios, obtenemos:
\begin{equation*}
\vec{F}=-2.31\times 10^{-14}\,\text{N}\,\hat{\textbf{k}}.
\end{equation*}
b) Usando la Segunda Ley de Newton, tenemos:
\begin{equation*}
\sum\vec{F}=m\vec{a},
\end{equation*}
que con valores numéricos da:
\begin{equation*}
\vec{a} \approx -1.38\times 10^{13}\,\text{m/s}^2\,\hat{\textbf{k}}.
\end{equation*}
c) La aceleración centrípeta es:
\begin{equation*}
a_c= \frac{v^2}{R},
\end{equation*}
donde despejando \(R \), e insertando los valores numéricos, obtenemos:
\begin{equation*}
R \approx 4.2\times 10^{-3}\,\text{m}.
\end{equation*}
d) La velocidad angular es:
\begin{equation*}
\omega=\frac{v}{R},
\end{equation*}
que, en nuestro caso, es igual a:
\begin{equation*}
\omega \approx5.7\times 10^{7}\,\text{rad/s}.
\end{equation*}
e) El período, en términos de velocidad angular, es:
\begin{equation*}
T=\frac{2\pi}{\omega}.
\end{equation*}
La distancia es simplemente la velocidad multiplicada por el tiempo, que es:
\begin{equation*}
\Delta x=v_xt.
\end{equation*}
El tiempo es el período que se encontró previamente. La distancia, numéricamente, entonces es:
\begin{equation*}
\Delta x \approx0.02\,\text{m}.
\end{equation*}
Para obtener una explicación más detallada de cualquiera de estos pasos, haga clic en “Solución detallada”.
[/mepr-show]
a) La fuerza ejercida sobre el protón \(\vec{F} \) debido al campo magnético en \(t = 0 \) se puede calcular usando la expresión para la fuerza de Lorentz (en ausencia de un campo eléctrico), a saber,
\begin{equation}
\label{force}
\vec{F}=q\vec{v}\times\vec{B},
\end{equation}
donde \(q \) es la carga de la partícula, \(\vec{v} \) es la velocidad en \(t = 0 \) y \(\vec{B} \) es el campo magnético. En nuestro caso, la partícula es un protón con carga \(q=e\approx 1.602\times 10^{-19}\,\text{C}\). Dado que el enunciado ya nos dió todas las variables que necesitamos para calcular esta fuerza, tenemos que
[mepr-show rules=”4409″ unauth=”both”]
\begin{equation}
\vec{F}=1.602\times 10^{-19}\,\text{C} (1.8\times 10^5\,\text{m/s}\,\hat{\textbf{i}}+2.4\times 10^5\,\text{m/s}\,\hat{\textbf{j>\times(0.6\,\text{T}\,\hat{\textbf{i>.
\end{equation}
Distribuimos los paréntesis para obtener los siguientes dos términos
\begin{equation}
\label{forceB}
\vec{F}\approx (1.73\times 10^{-14}\,\text{N})\,\hat{\text{i}}\times\hat{\textbf{i}}+(2.31\times10^{-14}\,\text{N})\,\hat{\textbf{j}}\times\hat{\textbf{i}}.
\end{equation}
Ahora aprovechamos que el producto cruzado entre vectores paralelos es siempre cero, es decir,
\begin{equation}
\label{ii}
\hat{\textbf{i}}\times\hat{\textbf{i}}=0.
\end{equation}
El producto cruzado entre dos vectores cartesianos unitarios diferentes es siempre otro vector cartesiano unitario, a saber
\begin{equation}
\label{ji}
\hat{\textbf{j}}\times\hat{\textbf{i}}=-\hat{\textbf{k}},
\end{equation}
donde el signo menos proviene de la regla de la mano derecha, como se ilustra aquí
Usamos la regla de la mano derecha para encontrar que \(\hat{\textbf{j}}\times\hat{\textbf{i}}=-\hat{\textbf{k}}\).
Usando los resultados de \eqref{ii} y \eqref{ji} en \eqref{forceB}, obtenemos nuestra respuesta:
\begin{equation}
\label{resulta}
\vec{F}=-2.31\times 10^{-14}\,\text{N}\,\hat{\textbf{k}}.
\end{equation}
b) La aceleración del protón se puede encontrar usando la segunda ley de Newton,
\begin{equation}
\label{secondlaw}
\sum\vec{F}=m\vec{a},
\end{equation}
donde \(\sum \vec{F} \) es la suma de todas las fuerzas que actúan sobre el protón, \(m \) es la masa del protón y \(\vec{a} \) es la aceleración del protón. Despejando \(\vec{a} \), encontramos
\begin{equation}
\vec{a}=\frac{\sum\vec{F}}{m}
\end{equation}
Dado que la masa del protón es extremadamente baja, podemos ignorar los efectos de la gravedad y, por lo tanto, la única fuerza relevante que actúa sobre el protón es la debida al campo magnético. Entonces, usando nuestro resultado de la ecuación \eqref{resulta} y el valor numérico de la masa del protón \(m_p = 1.67 \times 10^{-27} \,\text{kg} \), encontramos
\begin{equation}
\label{resultb}
\vec{a}=\frac{-2.31\times 10^{-14}\,\text{N}\,\hat{\textbf{k}}}{1.67\times 10^{-27}\,\text{kg}}\approx -1.38\times 10^{13}\,\text{m/s}^2\,\hat{\textbf{k}}.
\end{equation}
c) Para encontrar el radio de la trayectoria elíptica, primero debemos hacer un diagrama de cuerpo libre del protón. Como hemos visto antes, la única fuerza relevante es la debida al campo magnético. Esta fuerza genera una aceleración que afecta solo la dirección de la velocidad , no su magnitud (no afecta la magnitud porque la fuerza es perpendicular a la velocidad debido al producto cruzado). De hecho, la aceleración siempre se dirige hacia el centro de la trayectoria helicoidal, como se muestra aquí:
A la izquierda tenemos el dibujo original. A la derecha vemos la trayectoria desde la perspectiva del plano YZ. Usamos la regla de la mano derecha para mostrar que la fuerza magnética siempre apunta hacia el centro del círculo (es perpendicular tanto a \(v_ \perp \) como al campo magnético \(\vec{B} \)).
Para apreciar mejor que la fuerza siempre es radialmente hacia adentro, consideremos tres puntos arbitrarios, que se muestran en la siguiente imagen.
Diagrama que muestra diferentes puntos en la trayectoria de la partícula desde la perspectiva del plano YZ. La fuerza siempre apunta radialmente hacia adentro.
La componente de la velocidad afectada por la aceleración es la perpendicular al campo magnético \(v_ \perp \) en la figura anterior. Centrándonos solo en el plano YZ, la partícula sigue una trayectoria circular, por lo que podemos usar la definición de la aceleración centrípeta en términos de la rapidez y el radio:
\begin{equation}
\label{acentr}
a_c= \frac{v^2}{R},
\end{equation}
donde \(a_c \) es la magnitud de la aceleración centrípeta, que se puede calcular considerando la magnitud de la ecuación \eqref{resultb} . La variable \(v \) es la magnitud de la velocidad tangencial relativa al movimiento circular. En nuestro caso, esto es \(v_\perp \), que en \(t = 0 \) apunta a lo largo del eje Y, como se ve en la segunda figura. Despejando \(R \) en la ecuación \eqref{acentr}, obtenemos
\begin{equation}
R=\frac{v_\perp^2}{a_c}.
\end{equation}
Usando los valores numéricos para \(a_c \) y \(v_\perp \), finalmente obtenemos
\begin{equation}
R=\frac{(2.4 \times 10^5 \, \text{m/s})^2}{1.38\times 10^{13}\,\text{m/s}^2}\approx 4.2\times 10^{-3}\,\text{m}.
\end{equation}
d) Como ya tenemos la velocidad tangencial y el radio del movimiento circular, podemos calcular fácilmente su velocidad angular \(\omega \) usando la relación
\begin{equation}
\omega=\frac{v}{R},
\end{equation}
que en nuestro caso es igual a
\begin{equation}
\omega\approx\frac{2.4 \times 10^5 \, \text{m/s}}{4.2\times 10^{-3}\,\text{m}}\approx5.7\times 10^{7}\,\text{rad/s}.
\end{equation}
e) Finalmente, para encontrar la distancia recorrida a lo largo del eje X cuando ocurre una revolución, primero debemos encontrar el tiempo que se tarda en hacer una revolución. Este tiempo es el período del movimiento circular y está relacionado con la rapidez angular a través de la siguiente ecuación
\begin{equation}
\label{period}
T=\frac{2\pi}{\omega}.
\end{equation}
Como queremos calcular la distancia recorrida a lo largo del eje X \(\Delta x \), y no hay aceleración a lo largo de este eje, sabemos por la cinemática que la distancia es solo la rapidez multiplicada por el tiempo, es decir
\begin{equation}
\label{cinematica}
\Delta x=v_xt.
\end{equation}
En nuestro caso, la velocidad largo del eje X es la que es paralela al campo magnético, es decir \(v_\parallel\). El tiempo que usaremos en la ecuación \eqref{cinematica} es el período \(T \). Entonces, usando la expresión para el período dada por la ecuación \eqref{period} en la ecuación \eqref{cinematica}, obtenemos
\begin{equation}
\Delta x=v_\parallel \frac{2\pi}{\omega}.
\end{equation}
Usando los valores numéricos, finalmente tenemos que
\begin{equation}
\Delta x=(1.8\times 10^5\,\text{m/s})\frac{2\pi}{5.7\times 10^7\,\text{rad/s}}\approx0.02\,\text{m}.
\end{equation}
[/mepr-show]
You need to be registered and logged in to take this quiz. Log in


Leave A Comment