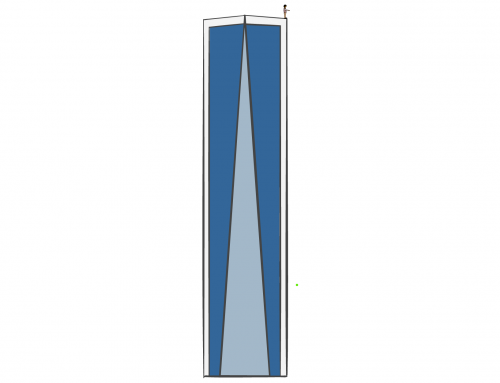
Una máquina utilizada en una línea de montaje ejerce diferentes fuerzas (ver figura) sobre una pieza de metal de 50 kg que se mueve en paralelo a la dirección de la fuerza.
Calcule el trabajo realizado por la máquina entre los siguientes puntos:
a) \(x=0 \,\text{m}\) y \(x=5 \,\text{m}\).
b) \(x=5 \,\text{m}\) y \(x=8 \,\text{m}\).
c) \(x=8 \,\text{m}\) y \(x=12 \,\text{m}\).
d) \(x=12 \,\text{m}\) y \(x=15 \,\text{m}\).
e) \(x=0 \,\text{m}\) y \(x=15 \,\text{m}\).
Suponga que la pieza está en reposo cuando está en \(x=0 \,\text{m}\). Usando el teorema trabajo-energía, calcule la rapidez de la pieza de metal en los siguientes puntos:
f) \(x=8 \,\text{m}\).
g) \(x=12 \,\text{m}\).
h) \(x=15 \,\text{m}\).
Para las partes (a), (b), (c) y (d), el área bajo la curva le dará el trabajo realizado.
Para la parte (e), esta es el área acumulada. Ya encontraste el trabajo.
Para las partes (f), (g) y (h), ya conoces cada trabajo realizado, por lo que puedes usar el teorema Trabajo-Energía para calcular la velocidad final en cada caso.
a) La forma integral del trabajo realizado es:
\begin{equation*}
W_{x_i\to x_f}=\int_{x_i}^{x_f}F_x\,dx,
\end{equation*}
[mepr-show rules=”4409″ unauth=”both”]
donde, de acuerdo con un gráfico de fuerza contra desplazamiento, significa que el trabajo se puede encontrar a partir del área bajo la curva. Geométricamente, es fácil encontrar cualquier área dividiendo la forma en rectángulos y triángulos, y considerando el signo verificando si la forma está colocada en el eje \({x-} \) positivo o el eje \({x-} \) negativo.
De \( x = 0 \, \text{m} \) a \( x = 5 \, \text{m} \), hay un triángulo. Entonces:
\begin{equation*}
W_{0\to5}=\frac{(5\,\text{m}-0\,\text{m})20\,\text{N}}{2}=50\,\text{J}.
\end{equation*}
b) De \(x = 5 \, \text{m} \) a \(x = 8 \, \text{m} \) hay un rectángulo. Entonces:
\begin{equation*}
W_{5\to8}=(8\,\text{m}-5\,\text{m})20\,\text{N}=60\,\text{J}.
\end{equation*}
c) De \(x = 8 \, \text{m} \) a \(x = 12 \, \text{m} \) hay dos triángulos. Entonces:
\begin{equation*}
W_{8\to12}=\frac{(10\,\text{m}-8\,\text{m})20\,\text{N}}{2}+\frac{(12\,\text{m}-10\,\text{m})(-20\,\text{N})}{2}=0\,\text{J}.
\end{equation*}
d) De \(x = 12 \, \text{m} \) a \(x = 15 \, \text{m} \) solo hay un triángulo. Entonces:
\begin{equation*}
W_{12\to15}=\frac{(15\,\text{m}-12\,\text{m})(-20\,\text{N})}{2}=-30\,\text{J}.
\end{equation*}
e) Desde \( x = 0 \, \text{m} \) a \( x = 15 \, \text{m} \), es fácil sumar los trabajos encontrados en cada parte anterior. Esta suma da:
\begin{equation*}
W_{0\to15}=80\,\text{J}.
\end{equation*}
f) Usemos el teorema Trabajo-Energía ( \( W = \Delta K \)) para despejar \( v_f \), considerando que \( v_i = 0 \) en \( x = 0 \). Esto nos da la siguiente relación:
\begin{equation*}
v_f=\sqrt{\frac{2W_{0\to x_f}}{m}}.
\end{equation*}
El trabajo realizado de \(x = 0 \, \text{m} \) a \(x = 8 \, \text{m} \) es \(110 \, \text{J} \). Por lo tanto, la rapidez en \( x_f = 8 \, \text{m} \) es:
\begin{equation*}
v_f \approx 2.1 \, \text{m/s}.
\end{equation*}
g) El trabajo realizado de \(x = 0 \, \text{m} \) a \(x = 12 \, \text{m} \) también es \(110 \, \text{J} \). Por lo tanto, la rapidez en \( x_f = 12 \, \text{m} \) es también:
\begin{equation*}
v_f \approx 2.1 \, \text{m/s}.
\end{equation*}
h) El trabajo realizado de \(x = 0 \, \text{m} \) a \(x = 15 \, \text{m} \) es \(80 \, \text{J} \). Por lo tanto, la rapidez en \( x_f = 15 \, \text{m} \) es:
\begin{equation*}
v_f \approx 1.8 \, \text{m/s}.
\end{equation*}
[/mepr-show]
(a) Para calcular el trabajo \(W \) entre dos puntos cualesquiera \(x_i \) y \(x_f \), debemos usar el hecho de que el trabajo realizado por una fuerza está dado por el área encerrada por la curva de la fuerza en una gráfica de fuerza vs desplazamiento. Más específicamente, el trabajo de una fuerza a lo largo de un desplazamiento a lo largo del eje X se define como
\begin{equation}
W_{x_i\to x_f}=\int_{x_i}^{x_f}F_x\,dx,
\end{equation}
[mepr-show rules=”4409″ unauth=”both”]
donde \(F_x \) es la fuerza aplicada a lo largo del eje X. Esta integral es igual al área bajo la curva dada en la gráfica \(F \) vs \(x \), donde el área se toma positiva para \(F> 0 \) y negativa para \(F< 0 \). De \(x = 0 \, \text{m} \) a \(x = 5 \, \text{m} \), tenemos que encontrar el área del triángulo de altura \(20 \, \text{N} \) y base \((5 \, \text{m} -0 \, \text{m} ) \) como se muestra en la figura 1.
Figura 1: El trabajo del primer segmento corresponde al área del triángulo en gris.
Explícitamente, el área en cuestión es
\begin{equation}
\label{w05}
W_{0\to5}=\frac{(5\,\text{m}-0\,\text{m})20\,\text{N}}{2}=50\,\text{J}.
\end{equation}
(b) De \(x = 5 \, \text{m} \) a \(x = 8 \, \text{m} \), debemos encontrar el área del rectángulo de base \((8 \, \text{m} -5 \, \text{m} ) \) y altura \(20 \, \text{N} \), ilustrado en la figura 2.
Figura 2: El trabajo del segundo segmento corresponde al área del rectángulo en gris.
Esta área está claramente dada por
\begin{equation}
\label{w58}
W_{5\to8}=(8\,\text{m}-5\,\text{m})20\,\text{N}=60\,\text{J}.
\end{equation}
(c) De \(x=8\,\text{m}\) a \(x=12\,\text{m}\) debemos encontrar el área de dos triángulos: el primero, de \(x = 8 \, \text{m}\) a \(x=10\,\text{m}\), y el segundo de \(x = 10 \, \text{m}\) a \(x=12\,\text{m}\). Estos dos triángulos se muestran en la figura 3 y 4.
Figura 3: Este es el primer triángulo que necesitamos para encontrar el área del trabajo en este segmento.
Figura 4: Este es el segundo triángulo para el que necesitamos encontrar el área. El trabajo total para este segmento será la suma del área de ambos triángulos
El trabajo es entonces la suma de las áreas, teniendo en cuenta que la primera es positiva y la segunda es negativa. El primer triángulo tiene una altura de \(20 \, \text{N} \) y una base de \((10 \, \text{m} -8 \, \text{m} ) \). El segundo triángulo tiene una altura de \(- 20 \, \text{N} \) y una base de \((12 \, \text{m} -10 \, \text{m} ) \). De ahí el trabajo entre \(x = 8 \, \text{m} \) y \(x = 12 \, \text{m} \) es
\begin{equation}
\label{w812}
W_{8\to12}=\frac{(10\,\text{m}-8\,\text{m})20\,\text{N}}{2}+\frac{(12\,\text{m}-10\,\text{m})(-20\,\text{N})}{2}=0\,\text{J}.
\end{equation}
(d) De \(x = 12 \, \text{m} \) a \(x = 15 \, \text{m} \), debemos encontrar el área del triángulo de base \((15 \, \text{m} -12 \, \text{m} ) \) y altura \(- 20 \, \text{N} \) mostrado en la figura 5.
Figura 5: El área de este triángulo será el trabajo realizado durante este último tramo
\begin{equation}
\label{w1215}
W_{12\to15}=\frac{(15\,\text{m}-12\,\text{m})(-20\,\text{N})}{2}=-30\,\text{J}.
\end{equation}
(e) Para encontrar el trabajo total de \(x = 0 \, \text{m} \) a \(x = 15 \, \text{m} \), podemos sumar todos los trabajos anteriores, lo que equivale a sumar todas las áreas bajo la curva entre \(x = 0 \, \text{m} \) y \(x = 15 \, \text{m} \). Explícitamente, el área total es
\begin{equation}
W_{0\to15}=W_{0\to5}+W_{5\to8}+W_{8\to12}+W_{12\to15},
\end{equation}
que, después de usar las expresiones numéricas dadas por las ecuaciones \eqref{w05}, \eqref{w58}, \eqref{w812} y \eqref{w1215}, se convierte en
\begin{equation}
\label{w015}
W_{0\to 15}=50\,\text{J}+60\,\text{J}+0\,\text{J}+(-30\,\text{J})=80\,\text{J}.
\end{equation}
(f) El teorema trabajo-energía relaciona el trabajo total realizado sobre una partícula con su cambio en la energía cinética \(K \) mediante la expresión
\begin{equation}
\label{workenergy}
W_{x_i\to x_f}=K_f-K_i,
\end{equation}
donde \(K_i \) y \(K_f \) son las energías cinéticas en las posiciones \(x_i \) y \(x_f \) respectivamente. La expresión de la energía cinética en términos de masa \(m \) y rapidez \(v \) es
\begin{equation}
K=\frac{1}{2}mv^2.
\end{equation}
Por tanto, la ecuación \eqref{workenergy} se puede escribir como
\begin{equation}
W_{x_i\to x_f}=\frac{1}{2}mv_f^2-\frac{1}{2}mv_i^2.
\end{equation}
Dado que en \(x_i = 0 \, \text{m} \) la rapidez es \(v_i = 0 \, \text{m/s} \), podemos escribir
\begin{equation}
W_{0\to x_f}=\frac{1}{2}mv_f^2.
\end{equation}
Ahora resuelva para la rapidez en \(x_f \),
\begin{equation}
v_f^2=\frac{2W_{0\to x_f}}{m},
\end{equation}
y saque la raíz cuadrada en ambos lados para obtener
\begin{equation}
\label{vf}
v_f=\sqrt{\frac{2W_{0\to x_f}}{m}}.
\end{equation}
Para este caso \(x_f = 8 \, \text{m} \). Por lo tanto, para encontrar la rapidez en este punto, debemos encontrar \(W_{0\to8}\) . El trabajo realizado de \(0 \, \text{m} \) a \(8 \, \text{m} \) está dado por la siguiente suma
\begin{equation}
W_{0\to8}=W_{0\to5}+W_{5\to 8},
\end{equation}
que, después de usar los valores numéricos dados en las ecuaciones \eqref{w05} y \eqref{w58} , nos lleva a
\begin{equation}
W_{0\to 8}=50\,\text{J}+60\,\text{J}=110\,\text{J}.
\end{equation}
Entonces podemos usar la ecuación \eqref{vf} para llegar a
\begin{equation}
v_8=\sqrt{\frac{2W_{0\to8}}{m}},
\end{equation}
donde \(v_8 \) es la rapidez en \(x_f = 8 \, \text{m} \). Usando los valores numéricos, tenemos
\begin{equation}
v_8=\sqrt{\frac{2(110\,\text{J})}{50\,\text{kg}}},
\end{equation}
\begin{equation}
v_8\approx 2.1 \,\text{m/s}.
\end{equation}
(g) En este caso \(x_f = 12 \, \text{m} \). Para encontrar la rapidez en este punto, debemos encontrar \(W_{0 \to12} \). El trabajo realizado de \(0 \, \text{m} \) a \(12 \, \text{m} \) es entonces la siguiente suma:
\begin{equation}
W_{0\to12}=W_{0\to5}+W_{5\to 8}+W_{8\to 12},
\end{equation}
que después de usar los valores numéricos dados en las ecuaciones \eqref{w05} , \eqref{w58} y \eqref{w812} se convierte en
\begin{equation}
W_{0\to 8}=50\,\text{J}+60\,\text{J}+0\,\text{J}=110\,\text{J}.
\end{equation}
Entonces podemos usar la ecuación \eqref{vf} para llegar a
\begin{equation}
v_{12}=\sqrt{\frac{2W_{0\to12}}{m}},
\end{equation}
donde \(v_{12} \) es la rapidez en \(x_f = 12 \, \text{m} \). Usando los valores numéricos, tenemos
\begin{equation}
v_{12}=\sqrt{\frac{2(110\,\text{J})}{50\,\text{kg}}},
\end{equation}
\begin{equation}
v_{12}\approx 2.1 \,\text{m/s}.
\end{equation}
(h) Ahora tenemos \(x_f = 15 \, \text{m} \). Debemos usar el resultado de \(W_{0 \to15} \) para encontrar la rapidez en este punto. Entonces podemos usar la ecuación \eqref{vf} para llegar a
\begin{equation}
v_{15}=\sqrt{\frac{2W_{0\to15}}{m}},
\end{equation}
donde \(v_{15} \) es la rapidez en \(x_f = 15 \, \text{m} \). Usando el valor numérico para \(W_ {0 \to15} \) dado por la ecuación \eqref{w015} , obtenemos que
\begin{equation}
v_{12}=\sqrt{\frac{2(80\,\text{J})}{50\,\text{kg}}},
\end{equation}
\begin{equation}
v_{12}\approx 1.8 \,\text{m/s}.
\end{equation}
[/mepr-show]
You need to be registered and logged in to take this quiz. Log in




Leave A Comment