Curling

a) Utilice el teorema trabajo-energía para relacionar la distancia, la velocidad y el coeficiente de fricción. La segunda ley de Newton también puede resultar útil.

b) Utilice las relaciones encontradas en la parte (a) y divida las fuerzas que se deben a la fricción para ver si se puede cancelar algo.

c) La misma pista del la parte (a).

a) El teorema trabajo-energía establece que:

\begin{equation*}
\Delta K = W_{tot},
\end{equation*}

[mepr-show rules=”4409″ unauth=”both”]

donde el trabajo es realizado por la fuerza debida a la fricción: \(W_{tot} = -f_r d \) y \(f_r = \mu N \). Para despejar la fuerza normal, podemos despejar la Segunda Ley de Newton en la dirección \({y-} \) para obtener:

\begin{equation*}
N-mg=0.
\end{equation*}

Note que la velocidad final es igual a cero, entonces \(K_f = 0 \). Sustituyendo todo en la primera ecuación y despejando \(\mu\), obtenemos:

\begin{equation*}
\mu = \frac{v_i^2}{2 g d}.
\end{equation*}

Para el caso de las barredoras, \(d = 15 \, \text{m} \), podemos escribir que:

\begin{equation*}
\mu_{sweep} = 0.014,
\end{equation*}

y sin barredoras, \(d = 10 \, \text{m} \), podemos escribir:

\begin{equation*}
\mu_{sweep} = 0.020.
\end{equation*}

b) Respecto a la relación entre las fuerzas debidas a la fricción, y sabiendo que \(\mu \) es inversamente proporcional a \(d \), obtenemos:

\begin{equation*}
\frac{f_{r_{\text{sweep}}}}{f_{r_{\text{NonSweep}}}} = \frac{d_{\text{NoSweep}}}{d_{\text{sweep}}},
\end{equation*}

que con valores numéricos es:

\begin{equation*}
\frac{f_{r_{\text{sweep}}}}{f_{r_{\text{NonSweep}}}} = \frac{2}{3}.
\end{equation*}

c) Dado que \(f_r = \mu N \) y \(N = mg \) en esta situación, la fuerza debida a la fricción es directamente proporcional a la masa. Si la masa se duplica, entonces \(f_r \) también se duplica, lo que da:

\begin{equation*}
2 f_r = \mu (2 m) g.
\end{equation*}

Para obtener una explicación más detallada de cualquiera de estos pasos, haga clic en “Solución detallada”.

[/mepr-show]

a) Para encontrar el fricción cinética del hielo, debemos comenzar relacionando la fuerza de fricción producida por el hielo con las otras variables. Observe que conocemos la rapidez inicial (2 m/s), y también sabemos que la rapidez final es cero (ya que la piedra finalmente se detendrá). Por lo tanto, podemos calcular fácilmente el cambio en la energía cinética, que, según el teorema de trabajo-energía, debe ser igual al trabajo total sobre la piedra. Entonces, usando ese teorema y el cambio de energía cinética, podemos encontrar el trabajo realizado por la fuerza de fricción, y con eso encontrar el coeficiente de fricción.

El teorema trabajo-energía establece que

\begin{equation}
\label{Curling_teoremaTrabajoEnergia}
\Delta K = W_{tot},
\end{equation}

[mepr-show rules=”4409″ unauth=”both”]

donde \(\Delta K \) es el cambio en la energía cinética (\(\Delta K = K_f-K_i \)), y \(W_{tot} \) es el trabajo total en la piedra. Ahora, para encontrar el trabajo total, comencemos por identificar las fuerzas sobre la piedra.

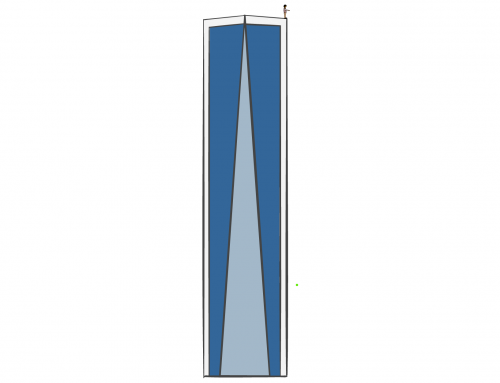
Una vez que se desliza, hay tres fuerzas sobre la piedra, el peso, la normal producida por el piso y la fricción cinética , como se ilustra en el diagrama de cuerpo libre de la figura 1 (observe que usamos un sistema de coordenadas con X apuntando en la dirección del movimiento de la piedra):

Figura 1: Diagrama de cuerpo libre de la piedra con tres fuerzas ejercidas sobre ella: la fuerza de contacto con el suelo \(\vec{N} \), el peso \(\vec{W} \) y la fricción \(\vec{f} _r \). El sistema de coordenadas se elige de manera que el eje X positivo sea paralelo a la trayectoria de la piedra. También incluimos el desplazamiento \(\vec{d} \) de la piedra, porque lo necesitaremos para encontrar el trabajo.

Ahora, para encontrar el trabajo total, necesitamos encontrar el trabajo producido por cada una de estas fuerzas. En general, el trabajo está dado por

\begin{equation}
W = \vec{F} \cdot \vec{d},
\end{equation}

donde \(\vec{F} \) es la fuerza y \(\vec{d} \) el vector de desplazamiento. Se puede escribir el producto escalar como

\begin{equation}
W = F d \cos \theta,
\end{equation}

donde \(\theta \) es el ángulo entre los dos vectores, y \(F \) y \(d \) sus magnitudes (sabemos que \(d \) es de 15 metros para el caso de las barredoras y de 10 metros sin las barredoras). Entonces, con esta ecuación, podemos encontrar la fuerza hecha por cada fuerza. En el diagrama, vemos claramente que tanto la fuerza normal como el peso son perpendiculares al desplazamiento, por lo que \(\theta \) es \(\pi / 2 \). También sabemos que \(\cos \pi / 2 = 0 \), lo que significa que estas fuerzas no realizan ningún trabajo sobre la piedra (esto siempre es cierto: las fuerzas perpendiculares al desplazamiento del cuerpo no hacen ningún trabajo) . Por tanto, la única otra fuerza que puede hacer trabajo es la fricción.

En el diagrama de cuerpo libre , vemos que la fricción es antiparalela al desplazamiento (apuntan en direcciones opuestas), lo que significa que el ángulo entre ellos es \(\pi \) y \( \cos \pi = -1\). Por eso,

\begin{equation}
W_{f_r} = – f_r d.
\end{equation}

El hecho de que el trabajo de la fricción sea negativo significa que el cuerpo está perdiendo energía debido a la acción de esta fuerza, lo que a su vez significa que la rapidez del cuerpo está disminuyendo debido a la fuerza.

Entonces, dado que la única fuerza que produce trabajo es la fricción, tenemos

\begin{equation}
W_{tot} = W_{f_r},
\end{equation}

y entonces

\begin{equation}
W_{total} = – f_r d.
\end{equation}

Usemos esto en la ecuación \eqref{Curling_teoremaTrabajoEnergia} para llegar a

\begin{equation}
\label{Curling_cineticaFriccion}
\Delta K = – f_r d.
\end{equation}

Para continuar, necesitamos encontrar \(f_r \). Sabemos que la fricción cinética viene dada por

\begin{equation}
\label{Curling_friccion}
f_r = \mu N,
\end{equation}

donde \(N \) es la magnitud de la fuerza normal producida por la superficie y \(\mu \) es el coeficiente de fricción cinética. Para encontrar \(N \), usemos la segunda ley de Newton a lo largo de Y. Dado nuestro diagrama de cuerpo libre , está claro que el peso es negativo en Y y la normal es positiva, por lo que tenemos

\begin{equation}
N \, \hat{\textbf{j}} – W \, \hat{\textbf{j}} = m a_y \, \hat{\textbf{j}}.
\end{equation}

Pero no hay aceleración en Y (solo en X), por lo que

\begin{equation}
N \, \hat{\textbf{j}} – W \, \hat{\textbf{j}} = 0 \, \hat{\textbf{j}}.
\end{equation}

Si usamos \(W = mg \) y nos enfocamos en las magnitudes, obtenemos

\begin{equation}
N – mg = 0.
\end{equation}

Por eso,

\begin{equation}
\label{Curling_normal}
N = mg.
\end{equation}

Si usamos esto en la ecuación \eqref{Curling_friccion} para obtener que

\begin{equation}
\label{Curling_friccionConMasa}
f_r = \mu (mg).
\end{equation}

Ahora podemos usar esto en la ecuación \eqref{Curling_cineticaFriccion} y llegar a

\begin{equation}
\Delta K = – (\mu mg) d.
\end{equation}

Finalmente tenemos una expresión donde la única variable desconocida es \(\mu \). Para usarlo, escribamos \(\Delta K \) explícitamente:

\begin{equation}
\frac{1}{2} m v_f^2 – \frac{1}{2} m v_i^2 = – \mu m g d.
\end{equation}

Sin embargo, la rapidez final es cero (la piedra se detiene), por lo que tenemos que

\begin{equation}
– \frac{1}{2} m v_i^2 = – \mu m g d.
\end{equation}

Si dividimos por \(-mgd \), obtenemos

\begin{equation}
\frac{-mv_i^2}{-2m g d} = \mu.
\end{equation}

La \(M \) y el \(- 1 \) se cancelan y obtenemos que

\begin{equation}
\label{Curling_mu}
\frac{v_i^2}{2gd} = \mu.
\end{equation}

Por último, introduzca aquí los valores numéricos para el caso con barredoras y el caso sin barredoras. Para las barredoras, \(d \) es de 15 metros, por lo que tenemos

\begin{equation}
\mu_{\text{sweep}} = \frac{(2 \, \text{m/s})^2}{2(9.8 \, \text{m/s}^2)(15 \, \text{m})},
\end{equation}

para obtener

\begin{equation}
\mu_{\text{sweep}} = 0.014.
\end{equation}

Si no hay barredoras, tenemos

\begin{equation}
\mu_{\text{NoSweep}} = \frac{(2 \, \text{m/s})^2}{2(9.8 \, \text{m/s}^2)(10 \, \text{m})},
\end{equation}

para obtener

\begin{equation}
\mu_{\text{NoSweep}} = 0.020.
\end{equation}

Estos resultados son intuitivos: todo el propósito de las barredoras es reducir la fricción entre la piedra y el hielo para que la piedra pueda moverse una distancia más larga. Además, ¡se necesita mucho entrenamiento para descubrir cuánto barrer para controlar la distancia recorrida por la piedra con alta precisión!

b) Ahora, queremos encontrar la relación entre la fuerza de fricción con barredoras y la fuerza de fricción sin barredoras. Es decir, la razón que queremos encontrar es

\begin{equation}
\label{Curling_cocientes}
\frac{f_{r_{\text{sweep}}}}{f_{r_{\text{NonSweep}}}}.
\end{equation}

Como explicamos antes, \(f_r = \mu N \). Observe que la fuerza normal no cambia entre los dos casos, ya que la fuerza normal viene dada por el peso (ver ecuación \eqref{Curling_friccion} arriba) y las barredoras no cambian el peso de la piedra (la masa no cambia). Entonces, lo único que cambia en los dos casos es \(\mu \):

\begin{equation}
f_{r_{\text{sweep}}} = \mu_{\text{sweep}} N,
\end{equation}

y

\begin{equation}
f_{r_{\text{NonSweep}}} = \mu_{\text{NoSweep}} N.
\end{equation}

Si usamos estas expresiones en \eqref{Curling_cocientes} , obtenemos

\begin{equation}
\frac{f_{r_{\text{sweep}}}}{f_{r_{\text{NonSweep}}}} = \frac{\mu_{\text{sweep}}N}{\mu_{\text{NoSweep}}N}.
\end{equation}

La fuerza normal se cancela y obtenemos

\begin{equation}
\frac{f_{r_{\text{sweep}}}}{f_{r_{\text{NonSweep}}}} = \frac{\mu_{\text{sweep}}}{\mu_{\text{NoSweep}}}.
\end{equation}

En este punto, el lector podría tener la tentación de usar los valores numéricos de los coeficientes encontrados en el punto (a), pero el resultado no sería tan preciso porque hay muchos dígitos decimales que tenemos que ignorar. De hecho, el lector podría verificar fácilmente que el resultado de usar los valores numéricos en esta ecuación es \(0.014 / 0.020 = 0.7 \), mientras que el resultado exacto, como veremos ahora, es \(2/3 \). Para el método exacto, use los resultados de la ecuación \eqref{Curling_mu} con las distancias correspondientes para obtener

\begin{equation}
\frac{f_{r_{\text{sweep}}}}{f_{r_{\text{NonSweep}}}} = \frac{\frac{v_i^2}{2gd_{\text{sweep}}}}{\frac{v_i^2}{2gd_{\text{NoSweep}}}}.
\end{equation}

La mayoría de los términos de la derecha se cancelan y obtenemos que

\begin{equation}
\frac{f_{r_{\text{sweep}}}}{f_{r_{\text{NonSweep}}}} = \frac{d_{\text{NoSweep}}}{d_{\text{sweep}}}.
\end{equation}

Si insertamos los valores numéricos, esto nos da

\begin{equation}
\frac{f_{r_{\text{sweep}}}}{f_{r_{\text{NonSweep}}}} = \frac{(10 \, \text{m})}{(15 \, \text{m})},
\end{equation}

y el resultado es

\begin{equation}
\frac{f_{r_{\text{sweep}}}}{f_{r_{\text{NonSweep}}}} = \frac{2}{3}.
\end{equation}

Claramente, la fricción disminuye.

c) ¿Qué le pasaría al valor de \(\mu \) si la masa de la piedra se duplicara?

Bueno, una forma de responder a esto es volviendo a la ecuación \eqref{Curling_mu} . Escribámosla aquí de nuevo

\begin{equation}
\label{Curling_muSegundo}
\mu = \frac{v_i^2}{2gd}.
\end{equation}

Observe que el coeficiente no depende de la masa, por lo que no cambiará si la masa se duplica. Pero en realidad ni siquiera necesitamos usar la ecuación \eqref{Curling_mu} para responder a esto. Conceptualmente, el coeficiente de fricción dinámica no depende de la masa de un objeto sino que solo depende del tipo de superficies de los materiales que están en contacto (en casos más avanzados, también puede depender de la temperatura de las superficies) . De hecho, el coeficiente es útil en el diseño de carreteras precisamente porque se puede estimar sin tener que tener en cuenta la masa particular de cada automóvil que pasa por encima.

Ahora bien, si la masa se duplica, es fácil ver que la magnitud de la fricción se duplica. Solo veamos la ecuación \eqref{Curling_friccionConMasa} eso demuestra que

\begin{equation}
f_r = \mu mg.
\end{equation}

Si la masa se duplica aquí, entonces \(f_r \) también se duplica:

\begin{equation}
2 f_r = \mu (2 m) g.
\end{equation}

[/mepr-show]

You need to be registered and logged in to take this quiz. Log in