Patinaje sobre Hielo

Utilice el teorema trabajo-energía donde el trabajo lo realiza la fuerza debida a la fricción y luego despeje el desplazamiento \(d \).

El teorema trabajo-energía establece:

\begin{equation*}
W = \Delta K.
\end{equation*}

[mepr-show rules=”4409″ unauth=”both”]

El trabajo realizado por la fuerza debida a la fricción es \(- f_r d \), pero la fuerza debida a la fricción es la mitad del peso que se indica en el problema. La última ecuación se puede escribir como:

\begin{equation*}
-\frac{mgd}{2}=\frac{1}{2}mv_f^2-\frac{1}{2}mv_i^2.
\end{equation*}

Despejando \(d \), obtenemos:

\begin{equation*}
d=\frac{v_f^2-v_i^2}{-g},
\end{equation*}

que con valores numéricos es:

\begin{equation*}
d \approx 4\, \text{m}.
\end{equation*}

[/mepr-show]

El problema nos pide que encontremos la longitud del parche áspero de hielo en el camino de la patinadora profesional. Para ello, debemos relacionar la longitud del camino con otras variables conocidas, como el cambio de rapidez por parte de la patinadora. Sabemos que el trabajo realizado por una fuerza está relacionado con el desplazamiento durante el cual actúa la fuerza, por lo que para encontrar la longitud en cuestión debemos encontrar el trabajo de las fuerzas relevantes. También sabemos que el trabajo total sobre un cuerpo está relacionado con el cambio de energía cinética y, por tanto, con el cambio de rapidez , mediante el teorema trabajo-energía. Por lo tanto, la clave para resolver este problema será encontrar primero una expresión para el trabajo neto sobre la patinadora y luego usar esa expresión en el teorema trabajo-energía, para resolver la longitud del parche de hielo.

El teorema trabajo-energía establece que

\begin{equation}
\label{workenergy}
W_{\text{net}}=K_f-K_i,
\end{equation}

[mepr-show rules=”4409″ unauth=”both”]

donde \(W_{\text{net}} \) es la suma de los trabajos realizados por todas las fuerzas ejercidas sobre la patinadora, o, equivalentemente, el trabajo realizado por la fuerza neta. Los términos \(K_i \) y \(K_f \) son las energías cinéticas antes y después del trabajo realizado por todas las fuerzas. En este caso, corresponden a las energías cinéticas justo al llegar al parche de hielo áspero (\(K_i \)), y justo después de dejarlo (\(K_f \)).

Para usar el teorema anterior, calculemos el trabajo neto realizado en la patinadora. Si un objeto se mueve a lo largo de una trayectoria descrita por un vector de desplazamiento \(\vec{d} \), entonces el trabajo ejercido por una fuerza \(\vec{F} \) sobre tal objeto se define como

\begin{equation}
\label{work}
W=\vec{F}\cdot\vec{d},
\end{equation}

donde el producto punto se define como \(\vec{F} \cdot \vec{d}= Fd \cos \theta \). Claramente, si la fuerza en cuestión es perpendicular al desplazamiento, el trabajo de esa fuerza es cero (porque \(\cos 90^{\circ} = 0 \)). Por lo tanto, solo necesitaremos encontrar el trabajo de las fuerzas que son paralelas o antiparalelas a la dirección del movimiento de la patinadora.

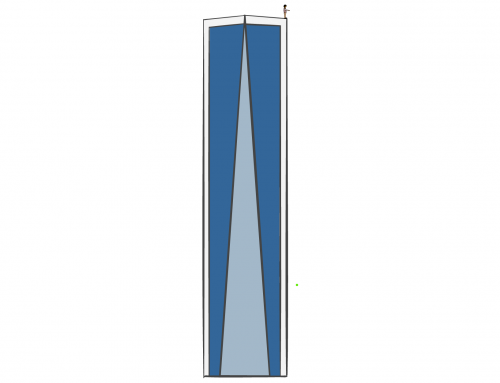
Sobre la patinadora, hay tres fuerzas en total; el peso apuntando hacia abajo, la fuerza normal con el suelo apuntando hacia arriba y la fricción cinética apuntando en contra de la dirección del movimiento. Si usamos un sistema de coordenadas donde X apunta a lo largo de la dirección del movimiento, se toma el diagrama de cuerpo libre de la figura 1.

Figura 1: Diagrama de cuerpo libre para la patinadora en el que se muestran tres fuerzas: la fuerza normal con el suelo, que es \(\vec{N} \), el peso \(\vec{W} = -mg \, \hat {\textbf{j} } \) y la fricción \(\vec{f} _r \). El desplazamiento \(\vec{d} \) también se muestra en azul. El sistema de coordenadas se elige de manera tal que el eje X apunta en la dirección del movimiento y el eje Y apunta hacia arriba.

Vemos que la única fuerza que va en la misma dirección del eje del vector de desplazamiento \(\vec{d} \) es la fricción \(\vec{f} _r \), que es antiparalela al desplazamiento. Las otras fuerzas (el peso y la fuerza normal) son perpendiculares al vector de desplazamiento y, por lo tanto, no contribuyen al trabajo neto. A partir del enunciado, también sabemos que la magnitud de la fricción es la mitad del peso \(mg \) de la patinadora sobre hielo. Aquí \(m \) es la masa de la patinadora y \(g \) la aceleración gravitacional de la tierra. Entonces podemos escribir la fuerza de fricción de la siguiente manera:

\begin{equation}
\vec{f}_r=-\frac{mg}{2}\,\hat{\textbf{i}},
\end{equation}

donde decimos que su dirección es negativa en X. Entonces, el trabajo realizado por la fricción es

\begin{equation}
\label{workdone}
W_{\text{fr}}=\vec{f}_r\cdot \vec{d},
\end{equation}

donde \(\vec{d} \) es el vector de desplazamiento, que en este caso tiene magnitud \(d \), la longitud del parche de hielo áspero y su dirección es la misma que el movimiento de la patinadora. Por tanto, podemos escribir el desplazamiento explícitamente como

\begin{equation}
\vec{d}=d\,\hat{\textbf{i}}.
\end{equation}

Usando las expresiones explícitas para la fuerza de fricción y el desplazamiento hacia atrás en la ecuación \eqref{workdone} , obtenemos que

\begin{equation}
W_{\text{fr}}=\left(-\frac{mg}{2}\,\hat{\textbf{i}}\right)\cdot \left(d\,\hat{\textbf{i}}\right),
\end{equation}

que, después de realizar el producto punto, es

\begin{equation}
W_{\text{fr}}=-\frac{mgd}{2}\,\hat{\textbf{i}}\cdot\hat{\textbf{i}}.
\end{equation}

La expresión anterior se puede simplificar aún más para

\begin{equation}
\label{network}
W_{\text{fr}}=W_{\text{net}}=-\frac{mgd}{2},
\end{equation}

donde usamos el hecho de que \(\hat{\textbf{i}}\cdot\hat{\textbf{i}} = 1 \) (esto proviene del hecho de que \(\textbf{i}\) es de magnitud 1 y es paralelo a sí mismo, por lo que el ángulo entre \(\textbf{i}\) y él mismo es cero, lo que conduce a \(\cos 0^{\circ} = 1 \)). Nótese que también usamos que esto es lo mismo que el trabajo neto) el peso y la normal no realizan trabajo, como se explicó anteriormente).

Antes de usar este trabajo neto en el teorema trabajo-energía, primero escribamos la energía cinética en términos de variables conocidas (la masa y la rapidez del patinador). La energía cinética es

\begin{equation}
K=\frac{1}{2}mv^2,
\end{equation}

donde \(m \) es la masa de la patinadora y \(v \) su rapidez . Remplazando esta expresión y la expresión explícita para el trabajo neto que se encuentra en la ecuación \eqref{network} en la ecuación \eqref{workenergy} , obtenemos que

\begin{equation}
-\frac{mgd}{2}=\frac{1}{2}mv_f^2-\frac{1}{2}mv_i^2,
\end{equation}

donde \(v_i \) y \(v_f \) son las magnitudes de las velocidades antes y después de que la patinadora pase por el parche áspero. Podemos simplificar esta expresión cancelando la masa \(m \) y el término \(1/2 \):

\begin{equation}
-gd=v_f^2-v_i^2.
\end{equation}

Resolviendo para \(d \), obtenemos

\begin{equation}
d=\frac{v_f^2-v_i^2}{-g},
\end{equation}

que numéricamente es

\begin{equation}
d=\frac{(5\,\text{m/s})^2-(8\,\text{m/s})^2}{-(9.8\,\text{m/s}^2)},
\end{equation}

\begin{equation}
d\approx 4\,\text{m}.
\end{equation}

[/mepr-show]

You need to be registered and logged in to take this quiz. Log in