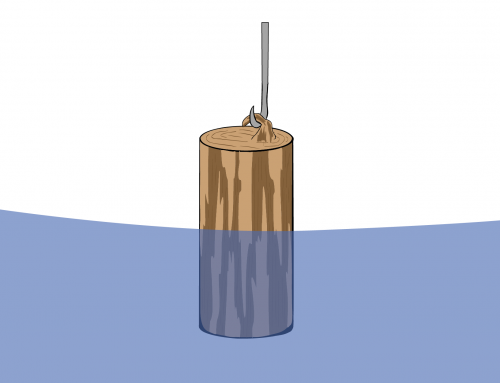
Un bloque de masa desconocida y volumen \(V\) está sujeto por una cuerda a una esfera de masa \(m\) y el mismo volumen \(V\). Ambos objetos se sumergen en agua. La esfera flota con la mitad de su volumen sobre la superficie mientras que el bloque se hunde por completo, dejando ambos equilibrados en configuración vertical. Calcula la masa del bloque.
Según la segunda ley de Newton para cada objeto, escriba las ecuaciones para relacionar las fuerzas (habrá dos ecuaciones con dos variables desconocidas). Para la fuerza de flotación, tenga cuidado con el volumen sumergido de cada objeto.
Para el equilibrio, la segunda ley de Newton establece:
\begin{equation*}
\sum F = 0,
\end{equation*}
[mepr-show rules=”4409″ unauth=”both”]
donde para el bloque completamente sumergido tenemos:
\begin{equation*}
F_{b,b} + T – Mg = 0,
\end{equation*}
que en este caso, la fuerza de flotación para este objeto es:
\begin{equation*}
F_{b,b} = \rho_w V g.
\end{equation*}
La segunda ley de Newton para la esfera es:
\begin{equation*}
F_{b,s} – T – mg = 0,
\end{equation*}
donde en este caso, la fuerza de flotación de la esfera es:
\begin{equation*}
F_{b,s} = \rho_w \frac{V}{2} g.
\end{equation*}
Resolviendo \(T\) en la ecuación anterior de la segunda ley de Newton obtenemos:
\begin{equation*}
T =\rho_w \frac{V}{2} g\, – mg,
\end{equation*}
y reemplazando en la otra ecuación, y despejando \(M\) tenemos:
\begin{equation*}
M = \frac{3}{2} \rho_w V – m,
\end{equation*}
Para obtener una explicación más detallada de cualquiera de estos pasos, haga clic en “Solución detallada”.
[/mepr-show]
Definamos \(M\) como la masa del bloque que deberíamos encontrar en términos de las otras variables conocidas. Podemos aplicar la segunda ley de Newton a la esfera y al bloque para relacionar estas variables con la masa \(M\) y finalmente resolverla.
Para usar la segunda ley de Newton, primero debemos definir un marco de referencia y dibujar el diagrama de cuerpo libre para cada cuerpo. La Figura 1 muestra el diagrama de fuerza para el bloque y nuestra elección de marco de referencia.
Figura 1: Diagrama de cuerpo libre para el bloque completamente sumergido que muestra las tres fuerzas ejercidas sobre él: la fuerza de flotación \(\vec{F}_{b,b}\), la tensión ejercida por la cuerda \(\vec{T} _c\) y el peso \(\vec{W}_c = -Mg \hat{\textbf{j}}\).
Observemos que, dado que hay una sola cuerda que conecta los dos objetos, la magnitud de cualquier tensión en la cuerda será la misma. Explícitamente,
\begin{equation}
\vec{T}_c=T \hat{\textbf{j}},
\end{equation}
donde hemos dejado caer deliberadamente el subíndice ya que solo hay una cuerda. De acuerdo con la figura 1, podemos escribir la segunda ley de Newton para el bloque como
[mepr-show rules=”4409″ unauth=”both”]
\begin{equation}
F_{b,b} \hat{\textbf{j}} + T \hat{\textbf{j}} – Mg \hat{\textbf{j}} = M a_b \hat{\textbf{j}},
\end{equation}
donde \(T\) es la magnitud de la tensión ejercida por la cuerda sobre el bloque, \(F_{b,b}\) es la magnitud de la fuerza de flotación ejercida por el agua, y \(a_b\) es la magnitud de su aceleración. Dado que todas las fuerzas actúan a lo largo de la dirección \(\hat{\textbf{j}}\) , solo podemos considerar sus magnitudes. Esto da
\begin{equation}
F_{b,b} + T – Mg = Ma_b.
\end{equation}
Ahora, el bloque está estacionario y por lo tanto \(a_b = 0 \), produciendo
\begin{equation}
F_{b,b} + T – Mg = 0.
\end{equation}
Si sumamos \(Mg\) en ambos lados de la ecuación, obtenemos
\begin{equation}
\label{EQ:n2l_b}
Mg = F_{b,b} + T.
\end{equation}
En última instancia, queremos resolver esta ecuación para M. Sin embargo, todavía necesitamos encontrar expresiones para la fuerza de flotación \(F_{b,b}\) y para la tensión T en términos de variables conocidas.
Encontremos primero la fuerza de flotación. Según el principio de Arquímedes, la magnitud de la fuerza de flotación ejercida por un fluido sobre un objeto es igual al peso del fluido desplazado por ese objeto \(w_{d,b}\) (es decir, el peso de la cantidad de fluido equivalente a la volumen del objeto). Podemos escribir esto como
\begin{equation}
F_{b,b} = w_{d,b},
\end{equation}
que por definición de peso, podemos reescribir como
\begin{equation}
\label{EQ:fbb}
F_{b,b} = m_{d,b} g.
\end{equation}
Aquí, \(m_{d,b}\) es la masa de agua desplazada por el bloque. A partir de la definición de densidad, podemos reescribir esta masa como
\begin{equation}
m_{d,b} = \rho_w V,
\end{equation}
donde \(\rho_w\) es la densidad del agua y \(V\) es el volumen del bloque, que es igual al volumen del agua que desplaza. Insertando esto en la ecuación. \eqref{EQ:fbb} obtenemos
\begin{equation}
F_{b,b} = \rho_w V g,
\end{equation}
y sustituyendo esta ecuación en la ecuación. \eqref{EQ:n2l_b} se cumple que
\begin{equation}
\label{EQ:block}
Mg = \rho_w V g + T.
\end{equation}
Ahora, para encontrar una expresión para \(T\), debemos aplicar la segunda ley de Newton en la esfera. La figura 2 muestra el diagrama de fuerza de la esfera.
Figura 2: Diagrama de cuerpo libre de la esfera que muestra las tres fuerzas ejercidas sobre ella: la fuerza de flotación \(\vec{F}_{b,s}\), la tensión de la cuerda \(\vec{T}_s = -T \hat{\textbf{j}}\) y el peso \(\vec{W}_s = -mg \hat{\textbf{j}}\).
De acuerdo con el diagrama de fuerza que se muestra en la figura 2, podemos escribir la segunda ley de Newton como
\begin{equation}
F_{b,s}\hat{\textbf{j}} – T \hat{\textbf{j}} – mg \hat{\textbf{j}} = m a_s \hat{\textbf{j}},
\end{equation}
donde \(T\) es la magnitud de la tensión ejercida por la cuerda sobre la esfera (que es la misma que la magnitud de la tensión ejercida sobre el bloque), \(F_{b,s}\) es la magnitud de la fuerza de flotación ejercida por el agua, y \(a_s\) es la magnitud de su aceleración.
Como en el caso del bloque, todas las fuerzas actúan a lo largo de la dirección \(\hat{\textbf{j}}\) , y la esfera está estacionaria. Por tanto, podemos considerar las magnitudes de los vectores de fuerza únicamente y establecer \(a_s = 0\). Esto da
\begin{equation}
\label{EQ:n2l_s}
F_{b,s} – T – mg = 0.
\end{equation}
Ahora, necesitamos encontrar la fuerza de flotación en la esfera \(F_{b,s}\). Como se explicó anteriormente para el bloque, \(F_{b,s}\) es igual a la magnitud del peso del agua desplazada por la esfera. Podemos escribir esto como
\begin{equation}
F_{b,s} = m_{d,s} g,
\end{equation}
donde \(m_{d,s}\) es la masa de agua desplazada por la esfera. Podemos reescribir la masa en términos del volumen \(V_{d,s}\) de agua desplazada por la esfera como
\begin{equation}
F_{b,s} = \rho_w V_{d,s} g.
\end{equation}
El volumen de agua desplazado por la esfera es igual al volumen de la esfera que está sumergida. Como la mitad de su volumen está sumergida, tenemos \(V_{d,s} = V/2\). Insertando esto en la ecuación anterior da
\begin{equation}
F_{b,s} = \rho_w \frac{V}{2} g.
\end{equation}
Ahora, sustituyendo esto en la ecuación. \eqref{EQ:n2l_s} se cumple que
\begin{equation}
\rho_w \frac{V}{2} g\, – T – mg = 0,
\end{equation}
y después de resolver \(T\), obtenemos
\begin{equation}
T =\rho_w \frac{V}{2} g\, – mg.
\end{equation}
Finalmente, sustituyendo esto en la ecuación. \eqref{EQ:block} obtenemos
\begin{equation}
Mg = \rho_w V g + \rho_w \frac{V}{2} g \, – mg.
\end{equation}
Observe que todos los términos tienen \(g\) como factores. Por lo tanto, si dividimos por \(g\) en ambos lados de la ecuación, se cancela, produciendo
\begin{equation}
M = \rho_w V + \rho_w \frac{V}{2} – m.
\end{equation}
Si factorizamos \(\rho_w V\) de los dos primeros términos en el lado derecho obtenemos
\begin{equation}
\label{EQ:M}
M = \rho_w V \left(1 + \frac{1}{2}\right) – m
= \frac{3}{2} \rho_w V – m,
\end{equation}
donde \(\rho_w, V\) y \(m\) son todas variables conocidas.
Observe que \(\frac{3}{2}\) \(V\) es el volumen sumergido total de los dos cuerpos (un volumen \(V\) del bloque y un volumen \(V/2\) de la esfera están sumergidos). Por lo tanto, \(\frac{3}{2} \rho_w V g\) es la fuerza de flotación total en ambos bloques. Consideremos ahora que los dos objetos conforman un solo sistema. Apliquemos la segunda ley de Newton, teniendo en cuenta las fuerzas que actúan sobre este sistema. Obtenemos
\begin{equation}
\frac{3}{2} \rho_w V g \, – (M+m)g = 0,
\end{equation}
donde el primer término representa la fuerza de flotación que actúa sobre ambos objetos y el segundo término representa el peso total. Si dividimos por g obtenemos
\begin{equation}
\frac{3}{2} \rho_w V – (M+m) = 0,
\end{equation}
y resolviendo para M obtenemos
\begin{equation}
M = \frac{3}{2} \rho_w V – m,
\end{equation}
que es lo mismo que la ecuación. \eqref{EQ:M}. Obtuvimos el mismo resultado de una manera mucho más simple al considerar ambos objetos como un solo sistema al aplicar la segunda ley de Newton.
[/mepr-show]


Leave A Comment