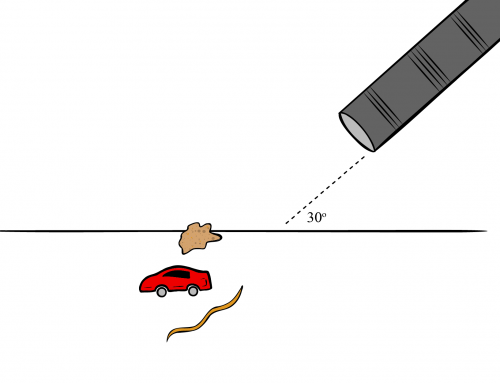
Car racing is a dangerous business, and it is imperative that race track architects understand principles of physics to ensure the safety of the race car drivers. The embankment must be properly positioned to withstand the cars’ potential to slide up the embankment. Suppose a 1,200 kg race car drives along a race track with a speed of 28 m/s, and the track can be approximated as a circle with a diameter of 500 meters.
(a) Assuming friction is negligible, calculate the bank angle \({\theta}\) necessary for the car to not slide, as shown in the figure.
(b) Realistically, friction is not negligible and must be taken into account. If the coefficient of static friction between the tires and the pavement is 0.2, calculate the minimum bank angle.
a) Draw a free body diagram, and note the \({x-}\) and \({x-}\)components of each force. When drawing the free body diagram, do not rotate the coordinate axes because there is an acceleration in the \({x-}\)direction pointing toward the center of the race track.
b) Same hint as part (a), but consider there is friction along both axes.
a) Newton’s Second Law in the \({y-}\)direction can be written as:
\begin{equation*}
N \cos \theta – mg = 0.
\end{equation*}
Newton’s Second Law in the \({x-}\)direction is:
\begin{equation*}
N \sin \theta = m a,
\end{equation*}
where \(a=\frac{v^2}{r}\). Solving for \(N\) in the first equation, substituting it into the last equation, and using some algebra, we get:
\begin{equation*}
\theta = \arctan \left( \frac{v^2}{rg} \right),
\end{equation*}
which, with numerical values, gives:
\begin{equation*}
\theta = 17.74^\circ.
\end{equation*}
b) Newton’s Second Law in the \({y-}\)direction can be written as:
\begin{equation*}
N \cos \theta – f_r \sin \theta -mg = 0.
\end{equation*}
Since \(f_r=\mu N\), we can solve for \(N\) in the previous equation to get:
\begin{equation*}
N = \frac{mg}{\cos \theta – \mu \sin \theta}.
\end{equation*}
Newton’s Second Law in the \({x-}\)direction can be written as:
\begin{equation*}
N \sin \theta + f_r \cos \theta = m a.
\end{equation*}
Using the previous result for \(N\), and after a lot of algebra, we get:
\begin{equation*}
\theta = \arctan \left( \frac{ \frac{v^2}{rg} – \mu } {1+\frac{v^2 \mu}{rg} } \right),
\end{equation*}
which, with numerical values, is:
\begin{equation*}
\theta = 6.43^\circ.
\end{equation*}
For a more detailed explanation of any of these steps, click on “Detailed Solution”.
a) In order to find the minimum bank angle necessary for the car to not slide, we must relate that angle to the mass of the car, the speed, and the radius of the circuit. It is key to bear in mind that we are dealing with an object moving in circles; therefore, the object will have radial or ‘centripetal’ acceleration. This type of acceleration points towards the center of the circle and comes from the fact that the direction of the object is constantly changing. This is because acceleration is a change in velocity and velocity is a vector. Hence, there will always be acceleration if the direction of velocity is changing. Once it is clear that this is a problem involving radial acceleration, we know that we can use Newton’s Second Law to relate this radial acceleration to the different forces, and by doing that we will be able to find the bank angle.
In order to apply Newton’s Second Law, let’s start by choosing a coordinate system. As it is common in problems of circular motion, we will use a coordinate system whose X axis (this is the radial axis, but we will call it X) points towards the center of the circle and whose Y axis points vertically, as indicated in figure 1.
Figure 1: We choose the coordinate system with the X axis pointing at all points at the center of the circular track and the positive Y axis pointing upwards.
The reason for using this system is that we are interested in the radial acceleration, which points along the X axis in this case. Of course, we could have used an inclined coordinate system like the ones used for inclined plane situations, but if we have done so the radial acceleration would not be aligned with the X axis and so we would have to find the different components of this acceleration, thus complicating the problem unnecessarily.
Now, there are only two forces acting on the car, the normal force produced by the floor, which is perpendicular to the floor, and the weight that points downwards. Notice that the weight is aligned with the Y axis, so we don’t need to find its components; however, the normal force isn’t aligned, and so it will have a Y and X component. Hence, the force diagram is shown in figure 2.
Figure 2: Force diagram for the car. The forces shown are the weight \(\vec{W}\) and the contact force \(\vec{N}\) which is perpendicular to the track. The angle between the contact force and the vertical is the same angle of inclination of the track.
Now that we have the force diagram, we can apply Newton’s Second Law. Along X there is only one force, namely, the X component of the normal force. So we get
\begin{equation}
\label{Slanted_FuerzasRadiales}
N_x \, \hat{\textbf{i}} = m a_x \, \hat{\textbf{i}},
\end{equation}
where \(N_x\) is the x component of the normal and \(a_x\) the acceleration in X (which points in the positive direction of X, towards the center of the circle).
Now, we want the minimum bank angle for the car to not slide. The reader might wonder if the condition for the car to not slide means that the acceleration \(a_x\) in equation \eqref{Slanted_FuerzasRadiales} must be zero. After all, when we have an inclined plane (and they do tell us that the object does not slide), we always use that the acceleration of the object is zero. This is a very common thought that we will address now.
When an object is just sitting on an inclined plane, there is no radial acceleration (the object is not moving in circles), and so the condition for not sliding means that the acceleration is indeed zero. In that case, the object will not go down the inclined plane. But if the object is on an inclined plane and at the same time it is moving in circles (as seen from ‘above,’ like in the case of the car), then the object will always have a non-zero acceleration, which is the radial acceleration that points towards the center of the circle. But even with an object that has this acceleration, it might still be true that the object will not slide over the inclined plane (this is the crucial difference with respect to the case where the object is just sitting on the inclined plane: in that case any non-zero acceleration means that the object will slide). For example, if the object is moving in circles very slowly, we know that it will start to go down, towards the bottom of the curve. And if the object starts to go down, then the radius of the circle that the object is tracing decreases (the object gets closer to the center of the circle as it moves towards the bottom of the curve). Or if the object is moving very fast, it will start to slide outwards and the radius will increase. This is illustrated in figure 3.
Figure 3: If the car slides, the radius of the circular trajectory will increase or decrease.
So, for a case of circular motion, the condition for not sliding is nothing more than the condition that the object keeps moving in a circle with a constant radius. In practical terms, this means that in a case of circular motion, we are allowed to use the radius of the circle given in the prompt when computing the radial acceleration (if the object was sliding, then we would not be allowed to use that radius). Notice that this is very different from the condition for not sliding in the case of an object sitting on an inclined plane, where no sliding meant ‘zero acceleration’.
Having said all this, we can go back to equation \eqref{Slanted_FuerzasRadiales} and take into account that the acceleration \(a_x\) is the radial acceleration, whose magnitude is given by
\begin{equation}
a_r=\frac{v^2}{r},
\end{equation}
where \(r\) is the radius of the circle and \(v\) the speed of the object. As we just explained, the condition for not sliding means that we are justified in assuming that the radius \(r\) used in this equation is not changing, and so it is precisely the radius of the circuit given in the prompt (250 meters). So, if we use this result in equation \eqref{Slanted_FuerzasRadiales}, we get
\begin{equation}
\label{Slanted_FuerzasRadiales2}
N_x \, \hat{\textbf{i}} = m \left( \frac{v^2}{r} \right) \, \hat{\textbf{i}}.
\end{equation}
Now, notice that the angle of the slanted curve that we need to find does not appear anywhere in this equation. But this is because that angle is `hidden’ in \(N_x\). From the force diagram, we see that
\begin{equation}
N_x = N \sin \theta,
\end{equation}
where \(\theta\) is the angle that we want to find. So let’s use this in equation \eqref{Slanted_FuerzasRadiales2} and focus on the magnitudes to get
\begin{equation}
\label{Slanted_FuerzaRadialParaReemplazar}
N \sin \theta = m \frac{v^2}{r} .
\end{equation}
We know the mass, the speed, and the radius, but we still need to find \(N\) in order to be able to find the angle. So we need more equations.
Consider the equations in Y. Along Y there are two forces, the Y component of the normal force, which is positive, and the weight, which is negative. So Newton’s Second Law in Y gives
\begin{equation}
N_y \, \hat{\textbf{j}} – W \, \hat{\textbf{j}} = m a_y \, \hat{\textbf{j}},
\end{equation}
where \(N_y\) is the Y component of the normal, \(W\) the weight, and \(a_y\) the vertical acceleration. Now, no sliding means that the car is not going up or down. This is the same as not changing the radius of the circle. If it were to go up, the radius would increase; if it were to go down, it would decrease. So, since our car is not going anywhere, we can use that \(a_y\) is zero:
\begin{equation}
\label{Slanted_fuerzasY}
N_y \, \hat{\textbf{j}} – W \, \hat{\textbf{j}} = 0 \, \hat{\textbf{j}}.
\end{equation}
Now, from the force diagram, we see that
\begin{equation}
N_y = N \cos \theta,
\end{equation}
and so equation \eqref{Slanted_fuerzasY} becomes
\begin{equation}
\label{Slanted_fuerzasY2}
N \cos \theta \, \hat{\textbf{j}} – W \, \hat{\textbf{j}} = 0 \, \hat{\textbf{j}}.
\end{equation}
Now let’s use that \(W=mg\), and let’s focus on the magnitudes:
\begin{equation}
N \cos \theta – mg = 0 .
\end{equation}
This is the same as
\begin{equation}
N \cos \theta = mg.
\end{equation}
If we divide by \(\cos\theta\), we get
\begin{equation}
N = \frac{mg}{\cos \theta}.
\end{equation}
So we can insert this result in equation \eqref{Slanted_FuerzaRadialParaReemplazar} to get
\begin{equation}
\left( \frac{mg}{\cos \theta} \right) \sin \theta = m \frac{v^2}{r}
\end{equation}
Since \( \sin \theta/ \cos \theta\) is \(\tan \theta\), this is the same as
\begin{equation}
mg \tan \theta = m \frac{v^2}{r}.
\end{equation}
If we cancel the mass and divide by \(g\) on both sides, we get
\begin{equation}
\tan \theta = \frac{v^2}{rg}.
\end{equation}
Hence, the angle is
\begin{equation}
\theta = \arctan \left( \frac{v^2}{rg} \right)
\end{equation}
If we insert the numerical values
\begin{equation}
\theta = \arctan \left( \frac{(28 \, \text{m/s})^2}{(250 \, \text{m})(9.8 \, \text{m/s}^2)} \right)
\end{equation}
we get
\begin{equation}
\theta = 17.74 ^\circ.
\end{equation}
b) Now we need to find the minimum bank angle assuming that there is an 0.4 static friction coefficient between the tires and the pavement. Due to this coefficient, we know that, in contrast to (a), there will be a friction force acting on the car. In what direction does this friction force point?
Well, if the car moves very rapidly, we know that the car will tend to slide ‘outwards’ (and if it goes even more rapidly it will drift and get into an accident). Since the static friction opposes the direction in which the object tends to move, then we infer that if the car moves very fast the static friction will point downwards parallel to the plane, as illustrated in figure 4.
Figure 4: If the car goes very fast it will drift outwards, and the friction will point inwards parallel to the track.
On the other hand, if the car moves slowly, it will tend to slide towards the bottom of the curve and so the friction in that case will point upwards parallel to the plane (see figure 5).
Figure 5: If the car goes very slow, it will slide inwards and the friction will be outwards parallel to the track.
Having said this, which is the direction of the friction that we care about in the present problem?
Well, notice that they ask us for the minimum bank angle. The smaller the angle, the easier for the object to slide outwards (this is why circuits for racing car have very steep curves). For example, if the angle is zero, the object will easily drift. As we increase the angle, we allow the car to move faster and faster without sliding, until reaching a point where the car is moving so fast that it will still drift. So we need to find that angle such that, for the given speed, the car still does not slide outwards. With this information, we can then infer that the static friction will point downwards parallel to the plane. So the force diagram is shown in figure 6.
Figure 6: Force diagram for the car at a speed such that the car tends to slide outwards but the friction exerted keeps in place. The forces shown are the weight \(\vec{W}\), the contact force \(\vec{N}\), and the friction \(\vec{f}_r\). Each force decomposed along the given X and Y axis using the angle \(\theta\).
Notice from the diagram, that the friction has a X component.
From this point onward, everything is very similar to what we did in (a). First, let’s write Newton’s Second Law in X, but now taking into account the new friction force. In X, this force has a positive component, as shown in the figure. Hence, we get
\begin{equation}
\label{primeraS}
N_x \, \hat{\textbf{i}} + f_{rx} \, \hat{\textbf{i}} = m a_x \, \hat{\textbf{i}},
\end{equation}
where \(N_x\) is the X component of \(N\), \(fr_x\) is the X component of the friction and \(a_x\) the X component of the acceleration. Now, from the force diagram we see that
\begin{equation}
N_x=N \sin \theta,
\end{equation}
and also that
\begin{equation}
fr_x=fr \cos \theta.
\end{equation}
Using these two expressions in \eqref{primeraS}, we get
\begin{equation}
N \sin \theta \, \hat{\textbf{i}} + f_r \cos \theta \, \hat{\textbf{i}} = m \frac{v^2}{r} \, \hat{\textbf{i}}.
\end{equation}
Now, the magnitude of the static friction can vary depending on the situation, but the maximum magnitude of such force is given by \(fr=\mu N \). Here we are interested in that maximum force because we are interested in the case where the car is about to slide outwards (and so in the case where the friction with the pavement is maximum). If we use this here, and focus on the magnitudes, we get:
\begin{equation}
N \sin \theta + \mu N \cos \theta = m \frac{v^2}{r}.
\end{equation}
Take common factor of \(N\):
\begin{equation}
\label{Slanted_FuerzaRadialConFriccionParaReemplazar}
N ( \sin \theta + \mu \cos \theta ) = m \frac{v^2}{r}.
\end{equation}
In order to continue, we need to find an expression for the normal force (which is different from the normal force in (a) because we have friction). From the diagram we see that in Y there are two forces, the Y component of the normal, pointing upwards, and the Y component of the friction, pointing downwards. So Newton’s Second Law in Y yields:
\begin{equation}
\label{segundaS}
N_y \, \hat{\textbf{j}} – f_{ry} \, \hat{\textbf{j}} – W \, \hat{\textbf{j}} = m a_y \, \hat{\textbf{j}}.
\end{equation}
Also from the diagram, we see that
\begin{equation}
N_y=N \cos \theta,
\end{equation}
and also that
\begin{equation}
fr_y=fr \sin \theta.
\end{equation}
Use these in \eqref{segundaS}, and also that the acceleration in Y is zero
\begin{equation}
N \cos \theta \, \hat{\textbf{j}} – f_{r} \sin \theta \, \hat{\textbf{j}} – W \, \hat{\textbf{j}} = 0 \, \hat{\textbf{j}}.
\end{equation}
Now use that \(fr=\mu N \), \(mg=W\) and focus on the magnitudes:
\begin{equation}
N \cos \theta – \mu N \sin \theta – mg = 0.
\end{equation}
Move the \(mg\) term to the other side and take common factor of \(N\):
\begin{equation}
N ( \cos \theta – \mu \sin \theta ) = mg.
\end{equation}
Now divide by \( ( \cos \theta – \mu \sin \theta ) \):
\begin{equation}
\label{Slanted_NormalConFriccion}
N = \frac{mg}{ \cos \theta – \mu \sin \theta }.
\end{equation}
Now that we have an expression for \(N\), use it in equation \eqref{Slanted_FuerzaRadialConFriccionParaReemplazar}:
\begin{equation}
\left( \frac{mg}{ \cos \theta – \mu \sin \theta } \right) (\sin \theta + \mu \cos \theta ) = m \frac{v^2}{r}.
\end{equation}
Let’s divide by \(g\) and cancel out the mass:
\begin{equation}
\frac{\sin \theta + \mu \cos \theta}{\cos \theta – \mu \sin \theta} = \frac{v^2}{rg}.
\end{equation}
We need to be able to extract \(\mu\) from this equation but right now the equation looks too complicated. It will be helpful to exploit some trigonometric identities. To do so, divide both the numerator and denominator in the left side by \( \cos \theta \):
\begin{equation}
\frac{\tan \theta + \mu}{1 – \mu \tan \theta} = \frac{v^2}{rg},
\end{equation}
where we used that \(\tan \theta= \sin \theta / \cos \theta\).
Let’s now multiply both sides by \( (1 – \mu \tan \theta)\):
\begin{equation}
\tan \theta + \mu = \frac{v^2}{rg} (1 – \mu \tan \theta).
\end{equation}
Open the parenthesis on the right:
\begin{equation}
\tan \theta + \mu = \frac{v^2}{rg} – \frac{v^2}{rg} \mu \tan \theta.
\end{equation}
Move the \(\frac{v^2}{rg} \mu \tan \theta\) term to the left and the \(\mu\) term to the right:
\begin{equation}
\tan \theta + \frac{v^2}{rg} \mu \tan \theta = \frac{v^2}{rg} – \mu.
\end{equation}
Now take common factor of \( \tan \theta \):
\begin{equation}
\tan \theta \left( 1 + \frac{v^2\mu}{rg} \right) = \frac{v^2}{rg} – \mu.
\end{equation}
Divide everything by \( \left( 1 + \frac{v^2\mu}{rg} \right) \):
\begin{equation}
\tan \theta = \frac{\frac{v^2}{rg} – \mu}{ 1 + \frac{v^2\mu}{rg} }
\end{equation}
We have then an expression for \( \theta \). Then,
\begin{equation}
\theta = \arctan \left( \frac{\frac{v^2}{rg} – \mu}{ 1 + \frac{v^2\mu}{rg} } \right).
\end{equation}
Finally, insert the numerical values.
\begin{equation}
\theta = \arctan \left( \frac{\frac{(28 \, \text{m/s})^2}{(250 \, \text{m})(9.8 \, \text{m/s}^2)} – (0.2)}{ 1 + \frac{(28 \, \text{m/s})^2(0.2)}{(250 \, \text{m})(9.8 \, \text{m/s}^2)} }\right)
\end{equation}
The result is \(\theta = 6.43^\circ\).
You need to be registered and logged in to take this quiz. Log in




Leave A Comment