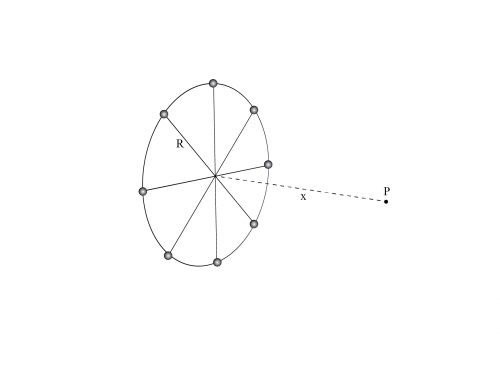
Suponga que tiene un cuarto de círculo que tiene una distribución de carga \(\lambda = \sec \theta \), como la que se muestra en la figura. Calcule el vector de campo eléctrico en el punto P.
PISTA
PRIMER PARRAFO Y PRIMERA ECUACION
[mepr-show rules=”4409″ unauth=”message”]
RESTO DE LA SOLUCION CORTA
[/mepr-show]
Para calcular el campo eléctrico \ (\ vec{E} \) producido por la distribución de carga, dividiremos la sección relevante del círculo en segmentos muy pequeños de carga \ (dq \) y longitud \ (ds \) (ver Figura 1 a continuación). Entonces, podemos considerar estos pequeños segmentos como cargas puntuales que producen un pequeño campo eléctrico \ (d \ vec{E} \) dado por la siguiente ecuación:
\begin{equation}
d \ vec{E} = \ frac{dq} {4 \ pi \ epsilon_0 r ^ 2} \, \ hat {\ textbf{r} },
\end{equation}
[mepr-show rules=”4409″ unauth=”message”]
donde \ (r \) es la distancia desde la carga \ (dq \) hasta el punto donde se calcula el campo eléctrico (P) y \ (\ hat {\ textbf{r}} \) es el vector unitario en la dirección del vector que va de la carga \ (dq \) al punto P. Como queremos el campo eléctrico para todo el segmento, necesitamos sumar todas las contribuciones de todas las cargas \ (dq \). Después de hacerlo, terminamos con la ecuación integral
\begin{equation}
\label{efield1}
\ int d \ vec{E} = \ int \ frac{dq} {4 \ pi \ epsilon_0 r ^ 2} \, \ hat {\ textbf{r} }.
\end{equation}
El lado izquierdo de la ecuación \ eqref{efield1} es el campo eléctrico \ (\ vec{E} \). Entonces,
\begin{equation}
\label{efield2}
\ vec{E} = \ int \ frac{dq} {4 \ pi \ epsilon_0 r ^ 2} \, \ hat {\ textbf{r} }.
\end{equation}
Ahora, para continuar y poder usar esta ecuación, necesitamos expresar el vector unitario \ (\ hat {\ textbf{r} } \) en términos de otras variables dadas por la geometría del problema. Primero, dibujaremos el vector \ (\ vec{r} \) como se ve en la siguiente figura:
Figura 1: Colocamos el sistema de coordenadas en el centro de la circunferencia. El campo eléctrico \ (\ vec{dE} \) generado por el diferencial de carga \ (dq \) de longitud \ (ds \) se muestra junto con el vector de distancia \ (\ vec{r} \). El campo se escribe en términos de sus componentes X e Y según el ángulo \ (\ theta \).
En general, para todos los cargos \ (dq \), el vector \ (\ vec{r} \) tiene una magnitud \ (r \) igual al radio del semicírculo \ (a \)
\begin{equation}
\label{ere}
r = a,
\end{equation}
y la dirección se dará en términos del ángulo \ (\ theta \), medido desde la vertical como se ve en la figura anterior. Entonces, podemos escribir
\begin{equation}
\label{vecere}
\ vec{r} = -a \ sin (\ theta) \, \ hat {\ textbf{i} } -a \ cos (\ theta) \, \ hat {\ textbf{j} }.
\end{equation}
El vector unitario \ (\ hat {\ textbf{r} } \) se puede calcular como la razón de \ (\ vec{r} \) y \ (r \). Explícitamente,
\begin{equation}
\label{runit}
\ hat {\ textbf{r} } = \ frac {\ vec{r} }{r} .
\end{equation}
Usando los resultados de las ecuaciones \ eqref{ere} y \ eqref{vecere} en la ecuación \ eqref{runit} , tenemos
\begin{equation}
\ hat {\ textbf{r} } = \ frac {-a \ sin (\ theta) \, \ hat {\ textbf{i} } -a \ cos (\ theta) \, \ hat {\ textbf{j} }}{a} ,
\end{equation}
que se convierte en
\begin{equation}
\label{runit2}
\ hat {\ textbf{r} } = – \ sin (\ theta) \, \ hat {\ textbf{i} } – \ cos (\ theta) \, \ hat {\ textbf{j} }.
\end{equation}
Usando el resultado de las ecuaciones \ eqref{ere} y \ eqref{runit2} en la ecuación \ eqref{efield2} , obtenemos
\begin{equation}
\label{efield3}
\ vec{E} = \ int \ frac{dq} {4 \ pi \ epsilon_0 a ^ 2} (- \ sin (\ theta) \, \ hat {\ textbf{i} } – \ cos (\ theta) \, \ hat {\ textbf{j} }).
\end{equation}
Se nos da la distribución de densidad de carga \ (\ lambda \), que en términos de \ (dq \) y \ (ds \) se puede escribir como
\begin{equation}
\ lambda = \ frac{dq}{ds},
\end{equation}
que se puede resolver para \ (dq \) para obtener
\begin{equation}
\label{dq}
dq = \ lambda \, ds.
\end{equation}
Debido a que \ (ds \) es una longitud de arco diferencial, se relaciona con el radio y un ángulo de arco diferencial \ (d \ theta \) de la siguiente manera
\begin{equation}
\label{ds}
ds = a \, d \ theta.
\end{equation}
Usando el resultado de la ecuación \ eqref{ds} en la ecuación \ eqref{dq} , finalmente obtenemos una expresión para \ (dq \) en términos de variables geométricas que podemos usar para integrar; a saber,
\begin{equation}
\label{dq2}
dq = \ lambda a \, d \ theta.
\end{equation}
Entonces podemos reemplazar \ (dq \) en la ecuación \ eqref{efield3} usando la expresión de la ecuación \ eqref{dq2} Llegar
\begin{equation}
\label{efield4}
\ vec{E} = \ int _ {\ theta_1} ^ {\ theta_2} \ frac {\ lambda a \, d \ theta} {4 \ pi \ epsilon_0 a ^ 2} (- \ sin (\ theta) \, \ hat {\ textbf{i} } – \ cos (\ theta) \, \ hat {\ textbf{j} }),
\end{equation}
donde los límites de la integral se dan en términos de los ángulos \ (\ theta_1 \) y \ (\ theta_2 \). Sacando los términos constantes en la ecuación \ eqref{efield4} y usando la expresión para la densidad de carga \ (\ lambda = \ sec (\ theta) \), obtenemos
\begin{equation}
\label{efield5}
\ vec{E} = \ frac{a} {4 \ pi \ epsilon_0 a ^ 2} \ int _ {\ theta_1} ^ {\ theta_2} d \ theta \ sec (\ theta) (- \ sin (\ theta) \, \ hat {\ textbf{i} } – \ cos (\ theta) \, \ hat {\ textbf{j} }).
\end{equation}
Usando la identidad trigonométrica \ (\ sec (\ theta) = \ frac{1} {\ cos (\ theta)} \), podemos escribir la ecuación \ eqref{efield5} como
\begin{equation}
\label{efield6}
\ vec{E} = \ frac{1} {4 \ pi \ epsilon_0 a} \ int _ {\ theta_1} ^ {\ theta_2} \ frac {d \ theta} {\ cos (\ theta)} (- \ sin (\ theta) \, \ hat {\ textbf{i} } – \ cos (\ theta) \, \ hat {\ textbf{j} }),
\end{equation}
donde también hemos cancelado la \ (a \) en el numerador con una \ (a \) en el denominador fuera de la integral.
Usando la ley distributiva en la ecuación \ eqref{efield6} , finalmente obtenemos
\begin{equation}
\label{efield7}
\ vec{E} = \ frac{1} {4 \ pi \ epsilon_0 a} \ int _ {\ theta_1} ^ {\ theta_2} d \ theta \ left (- \ frac {\ sin (\ theta)} {\ cos (\ theta)} \, \ hat {\ textbf{i} } – \ frac {\ cos (\ theta)} {\ cos (\ theta)} \, \ hat {\ textbf{j} }\derecho),
\end{equation}
que, después de la simplificación, se convierte en
\begin{equation}
\label{efield8}
\ vec{E} = \ frac{1} {4 \ pi \ epsilon_0 a} \ int _ {\ theta_1} ^ {\ theta_2} d \ theta \ left (- \ tan (\ theta) \, \ hat {\ textbf{i} } -1 \, \ hat {\ textbf{j} }\derecho).
\end{equation}
De la figura anterior, también podemos ver que los límites son \ (\ theta_1 = – \ pi / 4 \) y \ (\ theta_2 = \ pi / 4 \), por lo que debemos resolver la integral
\begin{equation}
\label{efield9}
\vec{E}=\frac{1}{4 \ pi \ epsilon_0 a} \ int _ {- \ frac {\ pi}{4}} ^ {\ frac {\ pi}{4}} d \ theta \ left (- \ tan (\ theta) \, \ hat {\ textbf{i}} -1 \, \ hat {\ textbf{j}}\right).
\end{equation}
Que se puede dividir de la siguiente manera
\begin{equation}
\label{efield10}
\vec{E}= – \ frac{1}{4 \ pi \ epsilon_0 a} \ left (\ int _ {- \ frac {\ pi}{4}} ^ {\ frac {\ pi}{4}} d \ theta \ tan (\ theta) \, \ hat {\ textbf{i}} + \ int _ {- \ frac {\ pi}{4}} ^ {\ frac {\ pi}{4}} d \ theta \, \ hat {\ textbf{j}}\right).
\end{equation}
Realizando las integrales que obtenemos
\begin{equation}
\vec{E}= – \ frac{1}{4 \ pi \ epsilon_0 a} \ left (\ ln | \ sec (\ theta) | \, \ hat {\ textbf{i}} + \ theta \, \ hat {\ textbf{j}} \ right) \ Big | _ {- \ frac {\ pi}{4}} ^ {\ frac {\ pi}{4}},
\end{equation}
que después de evaluar es
\begin{equation}
\vec{E}= – \ frac{1}{4 \ pi \ epsilon_0 a} \ left ((\ ln | \ sec (\ pi / 4) | – \ ln | \ sec (- \ pi / 4) |) \, \ hat {\ textbf{i}} + \ izquierda (\ frac {\ pi}{4}- \ izquierda (- \ frac {\ pi}{4}\ right) \ right) \, \ hat {\ textbf{j}}\right).
\end{equation}
El componente junto al eje X se cancela y luego obtenemos
\begin{equation}
\ vec{E} = – \ frac{1} {4 \ pi \ epsilon_0 a} \ left (0 \, \ hat {\ textbf{i} } + \ frac {\ pi}{2} \, \ hat {\ textbf{j} }\derecho).
\end{equation}
La expresión final para el campo eléctrico será entonces
\begin{equation}
\ vec{E} = – \ frac{1} {8 \ epsilon_0 a} \, \ hat {\ textbf{j} }.
\end{equation}
[/mepr-show]


Leave A Comment