¡Plano infinitamente cargado!

a) Use la ley de Gauss y calcule la distancia.

b) La misma pista que la parte (a).

La ley de Gauss establece:

\begin{equation*}
\oint_S \vec{E}\cdot d\vec{A}=\frac{Q_{\text{enc}}}{\epsilon_0},
\end{equation*}

[mepr-show rules=”4409″ unauth=”both”]

donde necesitamos dibujar una superficie gaussiana con forma cilíndrica. Dado que el cilindro tiene dos superficies circulares paralelas al plano, entonces tanto el campo eléctrico como el área deben multiplicarse por \(2\). En este caso, \(Q_{\text{enc}} = \sigma A\). Entonces:

\begin{equation*}
2EA=\frac{\sigma A }{\epsilon_0},
\end{equation*}

que se puede reescribir como:

\begin{equation*}
E=\frac{\sigma }{ 2 \epsilon_0}.
\end{equation*}

Observe que hay una dependencia \({no} \) de la distancia \(h \).

(a) El campo eléctrico es \(E = 80 \, \text{N/C} \).

(b) El campo eléctrico es \(E = 80 \, \text{N/C} \).

Para obtener una explicación más detallada de cualquiera de estos pasos, haga clic en “Solución detallada”.

[/mepr-show]

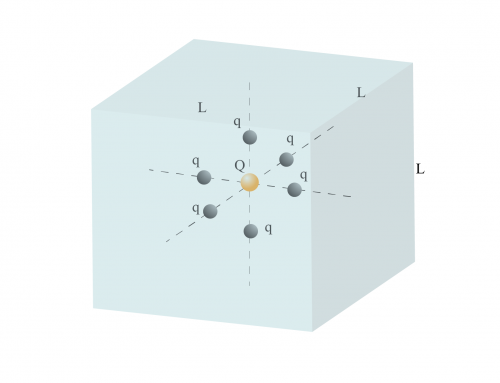
Necesitamos encontrar el campo eléctrico producido por un plano infinito al doble y la mitad de la distancia inicial dada. Para responder a ambas partes del problema, primero debemos encontrar una expresión general para el campo eléctrico de un plano infinito a una distancia arbitraria. Para encontrar este campo eléctrico, debemos usar la ley de Gauss y la simetría del campo que emerge del plano. Supondremos que el plano infinito tiene una densidad de carga superficial \(\sigma \) y está ubicado en el plano XY en \(z = 0 \). El campo eléctrico \(\vec{E} \) se dirige en el eje Z emergiendo del plano (asumiendo que \(\sigma> 0\)). Para \(z>0\), el campo eléctrico se dirige en el eje Z positivo, y para \(z<0 \) el campo eléctrico se dirige en el eje Z negativo. Para la superficie gaussiana, elegimos un cilindro con área \(A \) en su base y altura total \(2h \), como se puede ver en la figura 1.

[mepr-show rules=”4409″ unauth=”both”]

Figura 1: Plano infinitamente cargado (gris) a lo largo del plano XY y su campo eléctrico \(\vec{E} \) a lo largo del eje Z positivo y negativo. La superficie cilíndrica gaussiana (en dorado) también se muestra con su área transversal \(A \) y altura total \(2h \).

Ahora, podemos escribir la ley de Gauss.

\begin{equation} \label{gausslaw} \oint_S \vec{E}\cdot d\vec{A}=\frac{Q_{\text{enc}}}{\epsilon_0}, \end{equation}

donde la integral de flujo se realiza sobre la superficie cerrada \(S \), \(Q_{\text{enc} } \) es la carga encerrada por la superficie \(S \) y \(\epsilon_0 \) es una constante física conocida como la permitividad del espacio libre. El vector \(d \vec{A} \) es un vector cuya magnitud es el diferencial de superficie \(dA \) y su dirección es perpendicular al área de la superficie, siempre desde el interior hacia el exterior de la superficie por convención. Dividimos la integral dada en la ecuación \eqref{gausslaw} en tres integrales sobre tres superficies diferentes. Las superficies serán: la superficie circular en la parte superior \(S_1 \) (\(z> 0 \)), la superficie circular en la parte inferior \(S_2 \) (\(z< 0 \)), y la superficie curva que conecta las superficies circulares superior e inferior \(S_3 \). Entonces, podemos descomponer el lado izquierdo de la ecuación \eqref{gausslaw} como

\begin{equation}
\label{integral}
\oint_S\vec{E}\cdot d\vec{A}=\int_{S_1}\vec{E}_1\cdot d\vec{A}_1+\int_{S_2}\vec{E}_2\cdot d\vec{A}_2+\int_{S_3}\vec{E}_3\cdot d\vec{A}_3,
\end{equation}

donde, para cada integral, debemos elegir el vector apropiado \(d\vec{A} \) y campo eléctrico \(\vec{E} \) según cada superficie.

Primero, analicemos la integral sobre la superficie \(S_3 \). El vector \(d\vec{A} \) es diferente en cada punto; sin embargo, en todos los puntos de la superficie \(S_3 \) el vector está dirigido en el plano XY. Ya que el campo eléctrico siempre está dirigido en el eje Z (positivo o negativo), los vectores \(\vec{E_3} \) y \(d\vec{A}_3 \) son perpendiculares para todos los puntos de la superficie \(S_3 \); por lo tanto, el producto escalar entre estos vectores es siempre cero; a saber,

\begin{equation}
\vec{E}_3\cdot d\vec{A}_3=0.
\end{equation}

Como consecuencia, tenemos

\begin{equation}
\label{res3}
\int_{S_3}\vec{E}_3\cdot d\vec{A}_3=0.
\end{equation}

Ahora, examinemos la integral \(\int_{S_1} \vec{E}_1 \cdot d \vec{A}_1 \). En esta región, el campo eléctrico se puede escribir como

\begin{equation}
\vec{E_1}=E\,\hat{\textbf{k}},
\end{equation}

donde \(E \) es la magnitud del campo eléctrico a una distancia \(h \) del plano, como se muestra en la primera figura. El vector \(d\vec{A}_1 \) es perpendicular al área circular de la parte superior del cilindro, por lo que

\begin{equation}
d\vec{A}_1=dA_1\,\hat{\textbf{k}}.
\end{equation}

Haciendo el producto escalar entre el campo eléctrico y el vector de área, obtenemos

\begin{equation}
\label{dot1}
\vec{E}_1\cdot d\vec{A}_1=(E\,\hat{\textbf{k>\cdot(dA_1\,\hat{\textbf{k>=EdA_a\,\hat{\textbf{k}}\cdot \hat{\textbf{k}}=EdA_1,
\end{equation}

donde usamos el hecho de que \(\hat {\textbf{k}} \cdot \hat {\textbf{k}} = 1 \). Usando el resultado de la ecuación \eqref{dot1} para calcular la integral \(\int_{S_1} \vec{E}_1 \cdot d \vec{A}_1 \), obtenemos

\begin{equation}
\int_{S_1}\vec{E}_1\cdot d\vec{A}_1=\int_{S_1}E dA_1.
\end{equation}

Podemos extraer la magnitud del campo eléctrico \(E \) de la integral porque es constante. Entonces, terminamos con el resultado.

\begin{equation}
E\int_{S_1}dA_1=EA,
\end{equation}

donde en la última igualdad realizamos la integral \(\int_{S_1} dA_1 = A \), que es el área de la superficie circular superior. Por lo tanto,

\begin{equation}
\label{res1}
\int_{S_1}\vec{E}_1\cdot d\vec{A}_1=EA.
\end{equation}

Ahora, seguiremos un procedimiento similar para calcular la integral \(\int_{S_2} \vec{E}_2 \cdot d \vec{A}_2 \). Primero, en la región donde se encuentra \(S_2 \), el campo eléctrico se dirige en la dirección negativa del eje Z; entonces,

\begin{equation}
\label{e2}
\vec{E}_2=-E\,\hat{\textbf{k}}.
\end{equation}

donde \(E \) es la magnitud del campo eléctrico a una distancia \(h \) del plano infinito. Para el vector \(d\vec{A}_2 \), podemos escribir

\begin{equation}
\label{da2}
d\vec{A}_2=-dA_2\,\hat{\textbf{k}}.
\end{equation}

El vector \(d\vec{A}_2 \) se dirige hacia la dirección negativa del eje Z, porque es perpendicular a la superficie \(S_2 \) y se dirige desde el interior de la superficie hacia el exterior.

Usando las ecuaciones \eqref{e2} y \eqref{da2}, podemos realizar el producto escalar

\begin{equation}
\vec{E}_2\cdot d\vec{A}_2=(-E\,\hat{\textbf{k>\cdot(-dA_2\,\hat{\textbf{k>=EdA_2\,\hat{\textbf{k}}\cdot \hat{\textbf{k}},
\end{equation}

\begin{equation}
\label{dot2}
\vec{E}_2\cdot d\vec{A}_2=EdA_2,
\end{equation}

donde, en la última línea, usamos el hecho de que \(\hat {\textbf{k}} \cdot \hat {\textbf{k} } = 1 \).

Usando el resultado de la ecuación \eqref{dot2} para calcular la integral \(\int_{S_2} \vec{E}_2 \cdot d \vec{A}_2 \), obtenemos

\begin{equation}
\int_{S_2}\vec{E}_2\cdot d\vec{A}_2=\int_{S_2}E dA_2.
\end{equation}

Podemos extraer la magnitud del campo eléctrico \(E \) de la integral porque es constante, por lo que obtenemos el resultado

\begin{equation}
E\int_{S_2}dA_2=EA,
\end{equation}

donde en la última igualdad, realizamos la integral \(\int_{S_2} dA_2 = A \), que es el área de la superficie circular inferior; por lo tanto,

\begin{equation}
\label{res2}
\int_{S_2}\vec{E}_2\cdot d\vec{A}_2=EA.
\end{equation}

Poniendo los resultados de las ecuaciones \eqref{res3}, \eqref{res1} y \eqref{res2} en la ecuación \eqref{integral}, obtenemos

\begin{equation}
\label{oint}
\oint_S\vec{E}\cdot d\vec{A}=EA+EA+0=2EA.
\end{equation}

Ahora, dirigimos nuestra atención a calcular el lado derecho de la ecuación \eqref{gausslaw}, particularmente el término \(Q_{\text{enc}}\). En términos de la densidad de carga superficial \(\sigma \), podemos escribir la carga incluida como

\begin{equation}
\label{qenc}
Q_{\text{enc}}=\int \sigma dA.
\end{equation}

Ya que la densidad de carga superficial es constante, podemos extraerla de la integral en la ecuación \eqref{qenc} para obtener

\begin{equation}
Q_{\text{enc}}=\sigma\int dA.
\end{equation}

Realizando la integral anterior, obtenemos

\begin{equation}
\label{qenc2}
Q_{\text{enc}}=\sigma A,
\end{equation}

donde \(A \) es el área transversal de la superficie gaussiana, la que encierra la sección del plano infinito.

Poniendo los resultados de las ecuaciones \eqref{oint} y \eqref{qenc2} en la ecuación \eqref{gausslaw}, obtenemos

\begin{equation}
2EA=\frac{\sigma A}{\epsilon_0}.
\end{equation}

Cancelando el área \(A \) y despejando \(E \), obtenemos

\begin{equation}
E=\frac{\sigma}{2\epsilon_0}.
\end{equation}

Observe que la magnitud del campo eléctrico \(E \) no depende de \(h \), la distancia desde el plano infinito. Solo depende de la densidad de carga superficial \(\sigma \) y \(\epsilon_0 \), las cuales son constantes; por tanto, cuando se cambia la distancia, la magnitud del campo eléctrico no cambia. Por eso,

(a) El campo eléctrico es \(E = 80 \, \text{N/C} \).

(b) El campo eléctrico es \(E = 80 \, \text{N/C} \).

[/mepr-show]

You need to be registered and logged in to take this quiz. Log in or Register