Dos partículas están ubicadas en una región con un campo eléctrico de magnitud 700 N/C. La magnitud de la carga de ambas partículas es \(6.8\times 10^{-18}\,\text{C} \), pero una es positiva y la otra es negativa. La partícula positiva tiene 350 veces la masa de un protón, mientras que la partícula negativa tiene 500 veces la masa del electrón. Ignore la interacción entre las partículas y la fuerza gravitacional. Después de \(5 \mu s \) de liberar las partículas del reposo:
(a) Calcule la aceleración de cada partícula.
(b) Encuentre la posición de cada partícula.
(c) Calcule la rapidez de cada partícula.
a) Utilice la segunda ley de Newton para despejar \(a \) y sustituya las cantidades apropiadas para cada partícula.
b) Utilice la ecuación cinemática para despejar la posición, asumiendo que la aceleración y el tiempo son variables conocidas.
c) Use la ecuación cinemática para despejar la rapidez final en términos de la aceleración y el tiempo dado.
a) La segunda ley de Newton establece:
\begin{equation*}
\sum \vec{F}=m\vec{a},
\end{equation*}
[mepr-show rules=”4409″ unauth=”both”]
donde la única fuerza es la fuerza eléctrica, que se puede escribir como \(F_E = qE \). Entonces, despejando \(a \) obtenemos:
\begin{equation*}
\vec{a}=\frac{qE}{m}\,\hat{\textbf{i}}.
\end{equation*}
Con los valores dados, para la partícula negativa obtenemos:
\begin{equation*}
\vec{a}_{\text{neg}}\approx- 1.045\times 10^{13}\,\text{m/s}^2\,\hat{\textbf{i}}.
\end{equation*}
Para la partícula positiva:
\begin{equation*}
\vec{a}_{\text{pos}}\approx 8.144\times 10^{9}\,\text{m/s}^2\,\hat{\textbf{i}}.
\end{equation*}
b) Usando la ecuación cinemática:
\begin{equation*}
x_f=x_i+v_{x,i}t+\frac{1}{2}a_xt^2,
\end{equation*}
esto se puede reducir a:
\begin{equation*}
x_f=\frac{1}{2}a_xt^2.
\end{equation*}
Para la partícula negativa:
\begin{equation*}
x_f^{\text{neg}}\approx -131\,\text{m}.
\end{equation*}
Para la partícula positiva:
\begin{equation*}
x_f^{\text{pos}}\approx 0.102\,\text{m}.
\end{equation*}
c) Para encontrar la rapidez de cada partícula cuando ha pasado el tiempo \(t \), debemos usar la relación cinemática para una aceleración uniforme
\begin{equation}
\vec{v}_f=\vec{v}_i+\vec{a}t,
\end{equation}
donde con los valores dados, para la partícula negativa, obtenemos:
\begin{equation*}
v_{x,f}^{\text{neg}}\approx -5.225\times 10^{7}\,\text{m/s}.
\end{equation*}
Para la partícula positiva:
\begin{equation*}
v_{x,f}^{\text{pos}}\approx 4.072\times10^{4}\,\text{m/s}.
\end{equation*}
Para obtener una explicación más detallada de cualquiera de estos pasos, haga clic en “Solución detallada”.
[/mepr-show]
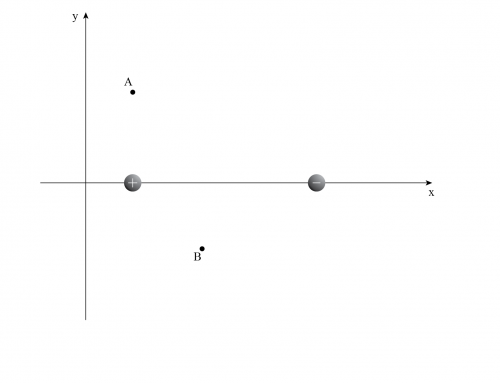
a) Para calcular la aceleración, debemos identificar todas las fuerzas relevantes ejercidas sobre las partículas y luego usar la segunda ley de Newton para encontrar la aceleración, entonces dibujemos las fuerzas ejercidas sobre cada partícula (ver figura 1).
Figura 1: diagrama de cuerpo libre para dos partículas cargadas. La única fuerza considerada es la fuerza eléctrica debido al campo eléctrico \(\vec{E} \). Colocamos el sistema de coordenadas de manera que el campo eléctrico esté orientado a lo largo del eje X positivo.
El campo eléctrico \(\vec{E} \) se puede escribir como su magnitud multiplicada por el vector unitario que indica su dirección; explícitamente,
\begin{equation}
\label{evec}
\vec{E}=E\,\hat{\textbf{i}}.
\end{equation}
Entonces podemos escribir la segunda ley de Newton como
\begin{equation}
\label{newton}
\sum \vec{F}=m\vec{a},
\end{equation}
donde \(m \) es la masa de la partícula, \(\vec{a} \) es el vector de aceleración y \(\sum \vec{F} \) es la suma de todas las fuerzas ejercidas sobre la partícula. Para ambas partículas, la única fuerza relevante será la fuerza eléctrica \(\vec{F}_E \), entonces la ecuación \eqref{newton} se convierte en
\begin{equation}
\label{newton2}
\vec{F}_E=m\vec{a}.
\end{equation}
La fuerza eléctrica viene dada por la carga multiplicada por el campo eléctrico; a saber,
\begin{equation}
\label{eforce}
\vec{F}_E=q\vec{E}.
\end{equation}
Usando la expresión de la fuerza eléctrica en la ecuación \eqref{newton2}, obtenemos
\begin{equation}
q\vec{E}=m\vec{a},
\end{equation}
donde podemos despejar la aceleración como
\begin{equation}
\label{acel}
\vec{a}=\frac{q}{m}\vec{E}.
\end{equation}
Usando la expresión para el campo eléctrico dada en la ecuación \eqref{evec} en la ecuación \eqref{acel}, obtenemos
\begin{equation}
\vec{a}=\frac{qE}{m}\,\hat{\textbf{i}}.
\end{equation}
Para la partícula cargada negativamente \(q = -6.8 \times 10^{-18}\,\text{C} \) y \(m = 500m_e \), donde \(m_e = 9.11 \times10^{-31}\,\text{kg} \); entonces, su aceleración es
\begin{equation}
\vec{a}_{\text{neg}}=\frac{(-6.8\times 10^{-18}\,\text{C})(700\,\text{N/C})}{500(9.11\times10^{-31}\,\text{kg})}\,\hat{\textbf{i}},
\end{equation}
\begin{equation}
\label{aneg}
\vec{a}_{\text{neg}}\approx- 1.045\times 10^{13}\,\text{m/s}^2\,\hat{\textbf{i}}.
\end{equation}
Tenga en cuenta aquí que el signo negativo indica que la dirección de la partícula cargada negativamente es hacia el eje X negativo, lo que significa que se opone al campo eléctrico.
Para la partícula con carga positiva \(q = 6.8 \times 10^{-18} \,\text{C} \) y \(m = 350m_p \), donde \(m_p = 1.67 \times 10^{-27} \,\text{kg} \); por lo tanto, su aceleración es
\begin{equation}
\vec{a}_{\text{pos}}=\frac{(6.8\times 10^{-18}\,\text{C})(700\,\text{N/C})}{350(1.67\times10^{-27}\,\text{kg})}\,\hat{\textbf{i}},
\end{equation}
\begin{equation}
\label{apos}
\vec{a}_{\text{pos}}\approx 8.144\times 10^{9}\,\text{m/s}^2\,\hat{\textbf{i}}.
\end{equation}
b) Ahora, calculemos la posición final de cada partícula. De los resultados de la aceleración encontrados en la parte (a) y teniendo en cuenta que las partículas se liberan desde el reposo podemos afirmar lo siguiente: la partícula positiva comienza a moverse en la dirección del campo eléctrico \(\hat{\textbf{i}} \), mientras que la carga negativa comienza a moverse en la dirección opuesta al campo eléctrico, a saber \(-\hat{\textbf{i}} \).
Suponga que ambas partículas comienzan en \(x = 0 \). El vector de posición \(\vec{r} \) en función del tiempo \(t \) en el caso uniformemente acelerado se puede escribir como
\begin{equation}
\vec{r}_f=\vec{r}_i+\vec{v}_it+\frac{1}{2}\vec{a}t^2,
\end{equation}
donde \(\vec{v}_i \) es la velocidad inicial y \(\vec{r}_i \), \(\vec{r}_f \) son los vectores de posición inicial y final respectivamente. Debido a que el movimiento ocurre solo en el eje X, podemos escribir la ecuación anterior como
\begin{equation}
x_f\,\hat{\textbf{i}}=x_i\,\hat{\textbf{i}}+v_{x,i}t\,\hat{\textbf{i}}+\frac{1}{2}a_x t^2\,\hat{\textbf{i}},
\end{equation}
u omitiendo la notación vectorial
\begin{equation}
\label{position}
x_f=x_i+v_{x,i}t+\frac{1}{2}a_xt^2,
\end{equation}
donde \(a_x \) es la aceleración a lo largo del eje X. Debido a que la velocidad inicial es cero y la posición inicial también es cero (podemos asumir que la partícula está inicialmente en el origen), podemos escribir la ecuación \eqref{position} como
\begin{equation}
\label{pos2}
x_f=\frac{1}{2}a_xt^2.
\end{equation}
Para la partícula negativa usamos el valor de \(a_x = -1.045 \times 10^{13} \,\text{m/s}^2 \) como se indica en la ecuación \eqref{aneg}. La ecuación \eqref{pos2} para la carga negativa se convierte en
\begin{equation}
x_f^{\text{neg}}=\frac{1}{2}(-1.045\times 10^{13}\,\text{m/s}^2)(5\times 10^{-6}\,\text{s})^2,
\end{equation}
\begin{equation}
x_f^{\text{neg}}\approx -131\,\text{m}.
\end{equation}
Para la carga positiva, la aceleración viene dada por la ecuación \eqref{apos}, entonces \(a_x = 8.144 \times 10^{9} \,\text{m/s}^2 \); entonces, usando la ecuación \eqref{pos2} obtenemos
\begin{equation}
x_f^{\text{pos}}=\frac{1}{2}(8.144\times 10^{9}\,\text{m/s}^2)(5\times 10^{-6}\,\text{s})^2,
\end{equation}
\begin{equation}
x_f^{\text{pos}}\approx 0.102\,\text{m}.
\end{equation}
c) Para encontrar la rapidez de cada partícula cuando ha pasado el tiempo \(t \), debemos usar la relación cinemática para una aceleración uniforme
\begin{equation}
\vec{v}_f=\vec{v}_i+\vec{a}t,
\end{equation}
donde \(\vec{v}_f \) es la velocidad final y \(\vec{v}_i \) es la velocidad inicial. Ya que el movimiento es a lo largo del eje X, podemos escribir la ecuación anterior como
\begin{equation}
v_{x,f}\,\hat{\textbf{i}}=v_{x,i}\,\hat{\textbf{i}}+a_xt\,\hat{\textbf{i}}.
\end{equation}
Omitiendo la notación vectorial en la ecuación anterior, obtenemos
\begin{equation}
v_{x,f}=v_{x,i}+a_xt,
\end{equation}
que se puede simplificar si sabemos que la velocidad inicial es cero; a saber,
\begin{equation}
\label{velocity}
v_{x,f}=a_xt.
\end{equation}
Por lo tanto, para la carga negativa, tenemos
\begin{equation}
v_{x,f}^{\text{neg}}=(-1.045\times 10^{13}\,\text{m/s}^2)(5\times 10^{-6}\,\text{s}),
\end{equation}
\begin{equation}
v_{x,f}^{\text{neg}}\approx -5.225\times 10^{7}\,\text{m/s}.
\end{equation}
Usando la ecuación \eqref{velocity} para la carga positiva, tenemos
\begin{equation}
v_{x,f}^{\text{pos}}=(8.144\times 10^{9}\,\text{m/s}^2)(5\times 10^{-6}\,\text{s}),
\end{equation}
\begin{equation}
v_{x,f}^{\text{pos}}\approx 4.072\times10^{4}\,\text{m/s}.
\end{equation}
[/mepr-show]


Leave A Comment