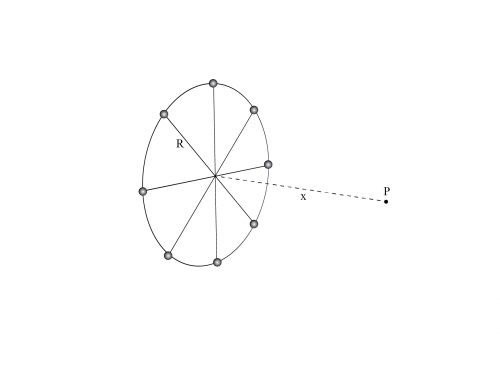
Una carga puntual \(Q = 8 \, \mu \text{C} \) está ubicada en el centro de un cubo de lado \(L = 0.3 \, \text{m} \). Seis cargas puntuales iguales (\(q = -2 \, \mu \text{C} \)) se colocan simétricamente alrededor de \(Q \), como se muestra en la figura.
(a) ¿Cuál es el flujo eléctrico neto a través del cubo?
(b) ¿Cuál es el flujo eléctrico a través de una cara del cubo?
(c) ¿Cuál es el flujo eléctrico a través del cubo si se elimina una de las cargas \(q \)?
(d) Siguiendo de (c), ¿es posible calcular el flujo eléctrico a través de una de las caras del cubo usando los mismos métodos?
a) Usando la ley de Gauss, el flujo eléctrico se obtiene directamente.
b) Piense en la simetría del problema.
c) La misma pista que en a).
d) La verdadera pregunta es: ¿qué pasa con la simetría?
a) Para encontrar el flujo eléctrico \(\Phi_E \) a través del cubo, usamos la ley de Gauss, de la siguiente manera:
\begin{equation*}
\Phi_E=\oint_S \vec{E}\cdot d \vec{A}=\frac{Q_\text{enc}}{\epsilon_0},
\end{equation*}
[mepr-show rules=”4409″ unauth=”both”]
donde \(Q_\text{enc} = Q + 6q\). Entonces, el flujo es:
\begin{equation*}
\Phi_E=\frac{Q + 6q}{\epsilon_0},
\end{equation*}
que con valores numéricos es:
\begin{equation}
\Phi_E \approx -4.5\times 10^5\,\text{V m}.
\end{equation}
b) Por simetría:
\begin{equation*}
\Phi_E^{\text{face}}=\frac{\Phi_E}{6}\approx-7.5\times 10^4\,\text{V m}.
\end{equation*}
c) Con una carga eliminada \(Q_\text{enc} = Q + 5q\). Entonces:
\begin{equation*}
\Phi_E=\frac{Q + 5q}{\epsilon_0},
\end{equation*}
que con valores numéricos es:
\begin{equation}
\Phi_E \approx -2.25\times 10^5\,\text{V m}.
\end{equation}
d) Se elimina una carga \(q \), por lo que se pierde la simetría. Por lo tanto, dividir por el número de caras ya no es válido y el flujo no podría calcularse solo en términos de las cargas encerradas. El flujo ahora dependerá de la posición relativa de las cargas con respecto a cada cara.
Para obtener una explicación más detallada de cualquiera de estos pasos, haga clic en “Solución detallada”.
[/mepr-show]
Para abordar este problema, usaremos la ley de Gauss para calcular el flujo en cada caso. Primero calculemos el flujo a través de todo el cubo y luego, usando la simetría del problema, deduzcamos el flujo a través de una de las caras del cubo.
a) Para encontrar el flujo eléctrico \(\Phi_E \) a través del cubo, usamos la ley de Gauss, como se escribe en la siguiente ecuación
\begin{equation}
\label{gausslaw}
\Phi_E=\oint_S \vec{E}\cdot d \vec{A}=\frac{Q_\text{enc}}{\epsilon_0},
\end{equation}
[mepr-show rules=”4409″ unauth=”both”]
donde la integral se toma sobre la superficie cerrada \(S \), \(\vec{E} \) es el campo eléctrico, \(Q_{\text{enc} } \) es la carga total encerrada por la superficie \(S \), y \(\epsilon_0 \) es una constante física llamada permitividad del espacio libre. Observe que, de la ecuación \eqref{gausslaw}, para calcular el flujo eléctrico a través de una superficie cerrada, todo lo que necesitamos saber es la carga encerrada por esa superficie; por lo tanto, podemos escribir la ley de Gauss como
\begin{equation}
\label{gausslaw2}
\Phi_E=\frac{Q_{\text{enc}}}{\epsilon_0}.
\end{equation}
Nuestra superficie gaussiana será la superficie del cubo. Entonces la carga encerrada por ella será la carga \(Q \) ubicada en el centro del cubo y las otras seis cargas \(q \) distribuidas simétricamente alrededor del centro del cubo; explícitamente,
\begin{equation}
\label{encq}
Q_\text{enc}=Q+6q.
\end{equation}
Usando el resultado de la ecuación \eqref{encq} en la ecuación \eqref{gausslaw2}, tenemos nuestra respuesta
\begin{equation}
\label{fluxa}
\Phi_E=\frac{Q+6q}{\epsilon_0}.
\end{equation}
Usando los valores numéricos, podemos calcular el flujo eléctrico neto a través de todo el cubo a partir de la ecuación \eqref{fluxa}; a saber,
\begin{equation}
\Phi_E=\frac{8\,\mu\text{C}+6(-2\,\mu\text{C})}{ 8.854 \times 10^{-12}\, \text{C/V m}},
\end{equation}
que se simplifica a
\begin{equation}
\Phi_E=\frac{-4\times 10^{-6}\,\text{C}}{8.854 \times 10^{-12}\, \text{C/V m}}\approx -4.5\times 10^{5}\,\text{V m}.
\end{equation}
El flujo es negativo, lo que indica que las líneas del campo eléctrico se dirigen desde el exterior del cubo hacia las cargas negativas.
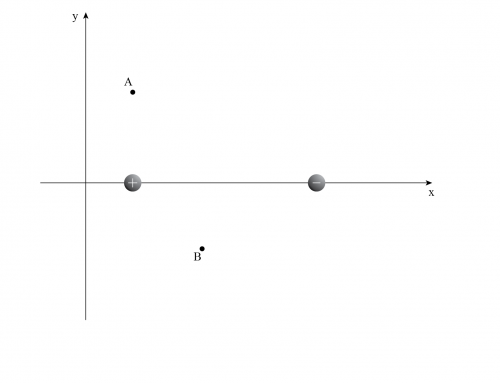
b) Para calcular el flujo en una de las caras del cubo, debemos usar un argumento de simetría. Observe que la configuración de las cargas es simétrica con respecto al centro del cubo. Debido a esta simetría, el flujo a través de cada cara del cubo es el mismo. Puede resultar útil ver el cubo desde la perspectiva de un lado, como se muestra en la figura 1.
Figura 1: Cubo desde la perspectiva de una cara.
El flujo total \(\Phi_E \), calculado en (a), es la suma del flujo a través de cada una de las seis caras, por lo que
\begin{equation}
\label{fluxface}
\Phi_E=6\Phi_E^{\text{face}},
\end{equation}
donde \(6 \Phi_E^{\text{face} } \) es el flujo de campo eléctrico a través de una sola cara. Resolviendo la ecuación \eqref{fluxface}, finalmente obtenemos
\begin{equation}
\Phi_E^{\text{face}}=\frac{\Phi_E}{6}\approx\frac{-4.5\times 10^5\,\text{V m}}{6}=-7.5\times 10^4\,\text{V m}.
\end{equation}
c) Si se elimina una de las cargas \(q \), entonces la carga encerrada por la superficie gaussiana cúbica será la carga \(Q \) colocada en el centro, más 5 cargas \(q \) distribuidas dentro del cubo; explícitamente,
\begin{equation}
\label{qenc2}
Q_{\text{enc}}=Q+5q.
\end{equation}
Entonces podemos usar las ecuaciones \eqref{gausslaw} y \eqref{qenc2} para calcular el nuevo flujo eléctrico como
\begin{equation}
\Phi_E=\frac{Q+5q}{\epsilon_0}.
\end{equation}
Usando los valores numéricos dados en el problema, obtenemos
\begin{equation}
\Phi_E=\frac{8\,\mu\text{C}+5(-2\,\mu\text{C})}{ 8.854 \times 10^{-12}\, \text{C/V m}},
\end{equation}
o, simplificando y usando notación científica
\begin{equation}
\Phi_E=\frac{-2\times 10^{-6}\,\text{C}}{8.854 \times 10^{-12}\, \text{C/V m}}\approx -2.25\times 10^{5}\,\text{V m}.
\end{equation}
Lo cual es nuevamente un flujo negativo, lo que indica que el flujo ingresa al cubo desde el exterior.
d) Si se elimina una de las cargas \(q \), se pierde la simetría alrededor del centro del cubo. Por lo tanto, la ecuación \eqref{fluxface} ya no es válida y el flujo no se pudo calcular solo en términos de las cargas encerradas. El flujo ahora dependerá de la posición relativa de las cargas con respecto a cada cara.
[/mepr-show]


Leave A Comment