Ideal Gas on an Unknown Cycle!

a) Use the given details to sketch the graph. Use ideal gas law in case you need something from the given variables.

b) Use the definition of work and sum all the works found.

a) The ideal gas law states:

\begin{equation*}
PV=nRT,
\end{equation*}

where the volumes are related as:

\begin{equation*}
V_1 = V_2 \text{; } V_3 = V_4 \text{ and } V_3 = 3V_1.
\end{equation*}

The temperatures are related as:

\begin{equation*}
T_1 = T_4 \text{ and } T_2 = T_3.
\end{equation*}

The pressure for point 3 and 4 is:

\begin{equation*}
P_4 = \frac{ P_3 }{2}
\end{equation*}

b) The definition of work is:

\begin{equation*}
W=\int_{V_i}^{V_f}P dV,
\end{equation*}

where is easy to get that \( W_{1\to2} = W_{3\to4} = 0\). Then:

\begin{equation*}
W_{2\to3}=2 nRT_1 \ln (3),
\end{equation*}

and

\begin{equation*}
W_{4\to1}=- nRT_1 \ln (3).
\end{equation*}

The total work is the sum of all the previous found works. Finally, we obtain:

\begin{equation*}
W_{\text{cycle}}= nRT_1 \ln (3),
\end{equation*}

or with numerical values:

\begin{equation*}
W_{\text{cycle}} \approx 6393.7 \, \text{J}.
\end{equation*}

For a more detailed explanation of any of these steps, click on “Detailed Solution”.

a) The problem asks us to sketch a diagram of the process, indicating the variables that are known. First, we are going to draw the diagram of each process to complete the cycle in a pressure-volume graph. We’ll justify the form of each process using ideal gas law

\begin{equation}
\label{idealg}
PV=nRT,
\end{equation}

where \(P\) is the absolute pressure in the gas, \(V\) its volume, \(n\) the number of moles, \(T\) the absolute temperature, and \(R\) the ideal gas constant.

In the whole process, the number of moles does not change, so \(n\) is a constant at all points.

If our starting point is 1, then as the temperature increases, the pressure increases with constant volume until we reach point 2, as can be seen from equation \eqref{idealg}. If \(V\) is constant, and \(nR\) is also a constant, then the pressure is directly proportional to temperature

\begin{equation}
\label{pt}
P\propto T.
\end{equation}

Afterward, an isothermal expansion occurs to reach point 3, thus decreasing the pressure and increasing the volume, as can be seen from equation \eqref{idealg}. If temperature \(T\) is constant and \(nR\) is also constant, then the pressure is inversely proportional to the volume

\begin{equation}
\label{pv}
P\propto\frac{1}{V}.
\end{equation}

From point 3 to point 4, we have a decrease in temperature at constant volume, thus the pressure must decrease accordingly to equation \eqref{pt}.

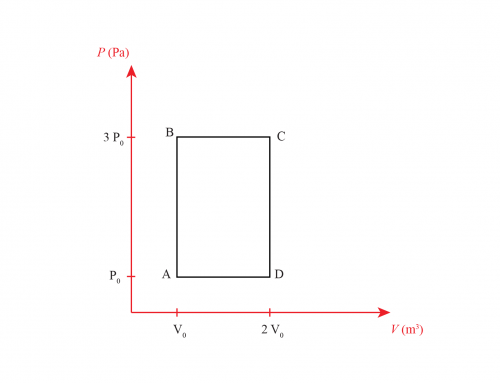
Finally, from point 4 back again to point 1 we have an isothermal compression, meaning the temperature is constant and as the volume decreases, pressure rises, as seen in the proportionality relation of equation \eqref{pv}; thus, we obtain the diagram shown in figure 1.

To find the relations between the variables, we must use the ideal gas law given in equation \eqref{idealg}. If we denote with a sub-index (1,2,3,4), each variable of state, then for point 1 we can write

\begin{equation}
\label{ideal1}
P_1V_1=nRT_1,
\end{equation}

where the only unknown is the volume which can be solved from \eqref{ideal1} to get

\begin{equation}
V_1=\frac{nRT_1}{P_1}.
\end{equation}

Between points 1 and 2 the volume does not change, thus

\begin{equation}
\label{v12}
V_1=V_2.
\end{equation}

In point 2 we don’t know the pressure or the temperature, so we won’t write any relation yet. Between points 2 and 3 there is an isothermal process, the temperatures must be the same, namely

\begin{equation}
T_2=T_3.
\end{equation}

Additionally, the problem states that the volume in point 3 is three times larger than the volume in point 1; then,

\begin{equation}
\label{v31}
V_3=3V_1.
\end{equation}

From point 3 to point 4 the gas does not change its volume; then,

\begin{equation}
\label{v34}
V_3=V_4.
\end{equation}

Additionally, the problem says the pressure is reduced by half between points 3 and 4; then,

\begin{equation}
\label{p34}
P_4=\frac{P_3}{2}.
\end{equation}

Finally, from point 4 to point 1 we have an isothermal process; thus, temperature at these two points must be the same. Explicitly,

\begin{equation}
\label{t41}
T_4=T_1.
\end{equation}

b) To calculate the work done by the gas \(W_{\text{cycle}}\) in one cycle 1-2-3-4-1, we can calculate the work of each process separately and then add it up; thus,

\begin{equation}
\label{workcycle}
W_{\text{cycle}}=W_{1\to2}+W_{2\to3}+W_{3\to4}+W_{4\to1}.
\end{equation}

Each work will be calculated using the following expression

\begin{equation}
\label{workexp}
W=\int_{V_i}^{V_f}P dV,
\end{equation}

where the integral is taken between an initial volume \(V_i\) and a final volume \(V_f\).

We’ll begin by calculating the term \(W_{1\to2}\) with equation \eqref{workexp}. Explicitly,

\begin{equation}
\label{int12}
W_{1\to2}=\int_{V_1}^{V_2}P dV.
\end{equation}

Because, according to equation \eqref{v12}, the volumes are equal; so, the integral in equation \eqref{int12} is zero because the lower and upper limit are the same, no change in volume takes place \(dV \to 0\).

\begin{equation}
\label{work12}
W_{1\to2}=0.
\end{equation}

Now, let’s calculate \(W_{2\to3}\), using \eqref{workexp} to get

\begin{equation}
\label{int23}
W_{2\to3}=\int_{V_2}^{V_3}PdV.
\end{equation}

Using the ideal gas law \eqref{idealg} to solve for pressure \(P\), we get

\begin{equation}
\label{idealP}
P=\frac{nRT}{V}.
\end{equation}

Using the expression in equation \eqref{idealP} into the integral given in equation \eqref{int23}, we obtain

\begin{equation}
\label{w23}
W_{2\to3}=\int_{V_2}^{V_3}\frac{nRT}{V}dV.
\end{equation}

We can take out the constant terms of the integral in equation \eqref{w23} to obtain

\begin{equation}
\label{w231}
W_{2\to3}=nRT\int_{V_2}^{V_3}\frac{dV}{V}.
\end{equation}

Performing the integral in equation \eqref{w231}, we obtain

\begin{equation}
\label{w232}
W_{2\to3}=nRT\ln\left(\frac{V_3}{V_2}\right),
\end{equation}

where the temperature \(T\) in equation \eqref{w232} can be either \(T_2\) or \(T_3\) because they are equal. Then, we can write explicitly

\begin{equation}
\label{w233}
W_{2\to3}=nRT_3\ln\left(\frac{V_3}{V_2}\right).
\end{equation}

Using relation given in equations \eqref{v12} and \eqref{v31}, we can replace \(V_2\) and \(V_3\) in terms of \(V_1\) in equation \eqref{w233}, namely

\begin{equation}
\label{234}
W_{2\to3}=nRT_3\ln\left(\frac{3V_1}{V_1}\right)=nRT_3\ln(3),
\end{equation}

where we have cancelled the term \(V_1\). Now, using the ideal gas law of equation \eqref{idealg} for point 3 we can replace the term \(nRT_3\) in equation \eqref{234} by \(P_3V_3\), thus obtaining

\begin{equation}
W_{2\to3}=P_3V_3\ln(3).
\end{equation}

To express this work in known given values by the problem, let’s use some relations deduced in part a). First we use equation \eqref{p34} to write \(P_3=2P_4\) and then

\begin{equation}
\label{work23}
W_{2\to3}=2P_4V_3\ln(3).
\end{equation}

Using equation \eqref{v34}, we can replace \(V_3\) by \(V_4\) in equation \eqref{work23}, obtaining

\begin{equation}
\label{work232}
W_{2\to3}=2P_4V_4\ln(3).
\end{equation}

Now, we’ll find an expression for \(P_4V_4\) in terms of known variables. Using the ideal gas law, we can solve for the temperature to obtain the expression

\begin{equation}
T=\frac{PV}{nR}.
\end{equation}

Using the expression above in the relation given in the left-hand side of equation \eqref{t41} to write

\begin{equation}
\frac{P_4V_4}{nR}=T_1,
\end{equation}

which, after solving for \(P_4V_4\), becomes

\begin{equation}
\label{p4}
P_4V_4=nRT_1.
\end{equation}

Now, we use the result for \(P_4V_4\) given in equation \eqref{p4} into equation \eqref{work232} to get

\begin{equation}
\label{work23f}
W_{2\to3}=2nRT_1\ln(3),
\end{equation}

which is given entirely in terms of known variables.

Now, we turn to calculate \(W_{3\to4}\) using the definition given in equation \eqref{workexp}, namely

\begin{equation}
W_{3\to4}=\int_{V_3}^{V_4}PdV.
\end{equation}

Once more, because there is no change in volume \(dV\to0\), the lower and upper limit of the integral are the same, so the work done is zero. Explicitly,

\begin{equation}
\label{work34}
W_{3\to4}=0.
\end{equation}

Finally, we calculate \(W_{4\to1}\) using the definition of equation \eqref{workexp}:

\begin{equation}
W_{4\to1}=\int_{V_4}^{V_1}PdV.
\end{equation}

Using the expression for \(P\) given in equation \eqref{idealP}, we can calculate

\begin{equation}
\label{w41}
W_{4\to1}=\int_{V_4}^{V_1}\frac{nRT}{V}dV.
\end{equation}

Because the process \(4\to1\) is isothermal the temperature is constant in all the process; thus, we can take out the constants outside the integral of equation \eqref{w41}. Explicitly,

\begin{equation}
\label{w41a}
W_{4\to 1}=nRT\int_{V_4}^{V_1}\frac{dV}{V},
\end{equation}

where \(T\) can be either \(T_1\) or \(T_4\). For convenience, let’s take \(T=T_1\), the known variable. Performing the integral in equation \eqref{w41a}, we get

\begin{equation}
\label{w41b}
W_{4\to1}=nRT_1\ln\left(\frac{V_1}{V_4}\right).
\end{equation}

From equations \eqref{v31} and \eqref{v34} we can deduce that \(V_4=3V_1\). Using this in equation \eqref{w41b}, we get

\begin{equation}
W_{4\to1}=nRT_1\ln\left(\frac{V_1}{3V_1}\right),
\end{equation}

which, after cancelling out \(V_1\), becomes

\begin{equation}
W_{4\to1}=nRT_1\ln\left(\frac{1}{3}\right).
\end{equation}

Using the properties of logarithms, we can rewrite the expression for \(W_{4\to1}\) as

\begin{equation}
\label{work41}
W_{4\to1}=-nRT_1\ln(3).
\end{equation}

Putting all the expressions for the work in each process given by equations \eqref{work12}, \eqref{work23f}, \eqref{work34} and \eqref{work41} into equation \eqref{workcycle}, we have

\begin{equation}
W_{\text{cycle}}=0+2nRT_1\ln(3)+0-nRT_1\ln(3),
\end{equation}

which is reduced to

\begin{equation}
W_{\text{cycle}}=nRT_1\ln(3).
\end{equation}

Using the numerical values, we have that

\begin{equation}
W_{\text{cycle}}=(2\,\text{mol})(8.314\,\text{J/mol K})(350\,\text{K})\ln(3),
\end{equation}

\begin{equation}
W_{\text{cycle}}\approx 6393.7\,\text{J}.
\end{equation}

You need to be registered and logged in to take this quiz. Log in or Register