Water Fountain!

Note that the power from the anvil must be equal to the power from the fountain’s pump. Relating these equations can lead you to solve for \(m\), and use the density of the water to find the volume.

To find the velocity, apply Conservation of Energy to get the answer.

a) Since power is equal to energy over time, this relationship can be written as:

\begin{equation*}
P = \frac{\Delta E}{\Delta t}.
\end{equation*}

In this case, we need to consider the gravitational potential energy in both cases. The power of the anvil and the fountain’s pump must be equal. Given that relation and solving for \(m\), we get:

\begin{equation*}
m=\frac{M\Delta H\Delta t_2}{h\Delta t_1},
\end{equation*}

where \(g\) cancels out.

Since the density is \(\rho = \frac{m}{V}\), we can solve for \(V\) to obtain:

\begin{equation*}
V=\frac{M\Delta H\Delta t_2}{\rho h\Delta t_1},
\end{equation*}

which, with numerical values, yields:

\begin{equation*}
V=0.4 \, \text{m}^3 = 400 \, \text{L}.
\end{equation*}

Now, for the velocity, Conservation of Energy gives:

\begin{equation*}
\frac{1}{2}mv^2=mgh.
\end{equation*}

Solving for \(v\), we get:

\begin{equation*}
v=\sqrt{2gh}.
\end{equation*}

Plugging in numerical values, we obtain:

\begin{equation*}
v=14\,\text{m/s}.
\end{equation*}

They are asking us to find the volume of the water that is ejected by the fountain every 2 seconds as well as its ejection speed. We will use the following approach to solve this problem:

• We will use the architect’s claim to calculate the power of the fountain. That is, the amount of energy per unit time that is capable of transferring to the water.
• With the given data of the normal operation of the fountain, we will calculate the power in terms of the mass of the chunk of water. From there, using the result for the power in step 1, we will solve for the mass of the chunk of water.
• We will use the density of water \(\rho\) to find the volume of water.
• Using the conservation of mechanical energy between the point at which the water is ejected and its maximum height, we will be able to find the speed at which the water is ejected.

Let us then first use the architect’s claim to find the power of the fountain \(P\). The power can be calculated in terms of energy as

\begin{equation}
\label{power}
P=\frac{\Delta E}{\Delta t},
\end{equation}

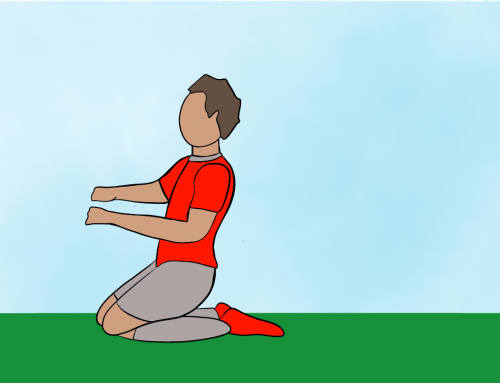
where \(\Delta E\) is the change of energy of the water and \(\Delta t\) is the amount of time during which this change of energy occurs. In our case, \(\Delta t_1=0.5\,\text{s}\) as the prompt indicates. The change of energy can be measured in this case as the change of gravitational potential energy of the anvil of mass \(M=1\,\text{Ton}=1000\,\text{kg}\) (see figure 1).

Figure 1: Water fountain lifting an anvil a vertical distance of \(\Delta H=\)1 m during a time interval \(\Delta t_1=\)0.5 s.

This change of energy has the following expression:

\begin{equation}
\Delta E=Mg\Delta H,
\end{equation}

where \(g=9.8\,\text{m/s}^2\) is the gravitational acceleration and \(\Delta H=1\,\text{m}\) is the distance that the anvil is lifted up. The power is then

\begin{equation}
\label{power1}
P=\frac{Mg\Delta H}{\Delta t_1}.
\end{equation}

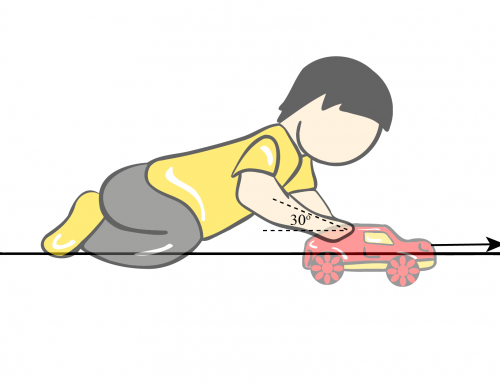
Now that we have the power of the fountain’s pump, we will use equation \eqref{power} to calculate the power for the normal operation of the fountain, where an amount of mass \(m\) of water is ejected and reaches a maximum height of \(h=10\,\text{m}\) (see figure 2). Thus, the change of energy \(\Delta E\) for this mass of water will be the change in the gravitational potential energy, explicitly

\begin{equation}
\Delta E=mgh.
\end{equation}

Figure 2: Mass of water \(m\) reaching its maximum height. The coordinate system is placed on the floor with the Y axis pointing upwards.

Because this amount of energy is delivered every 2 seconds, then \(\Delta t_2=2\,\text{s}\). The power for the normal operation mode is thus

\begin{equation}
\label{power2}
P=\frac{mgh}{\Delta t_2}.
\end{equation}

Because the power calculated in equation \eqref{power1} and \eqref{power2} is for the same fountain, they must be equal. Thus, we have

\begin{equation}
\frac{Mg\Delta H}{\Delta t_1}=\frac{mg h}{\Delta t_2},
\end{equation}

where we can solve for \(m\) to obtain

\begin{equation}
m=\frac{Mg\Delta H\Delta t_2}{\Delta t_1 g h}.
\end{equation}

We can cancel out the \(g\) in the expression above to finally get

\begin{equation}
\label{mass}
m=\frac{M\Delta H\Delta t_2}{h\Delta t_1}.
\end{equation}

Following up with step 3, we can use the relation between density of water \(\rho=1000\,\text{kg/m}^3\), mass and volume \(V\) given by the expression

\begin{equation}
\rho=\frac{m}{V},
\end{equation}

and solve for the volume to get

\begin{equation}
V=\frac{m}{\rho}.
\end{equation}

If we use the expression for the mass of water found in equation \eqref{mass} here, we obtain

\begin{equation}
V=\frac{M\Delta H\Delta t_2}{\rho h\Delta t_1}.
\end{equation}

Using the numerical values in SI units we get

\begin{equation}
V=\frac{(1000\,\text{kg})(1\,\text{m})(2\,\text{s})}{(1000\,\text{kg/m}^3)(10\,\text{m})(0.5\,\text{s})},
\end{equation}

\begin{equation}
V=0.4\,\text{m}^3=400\,\text{L},
\end{equation}

where we have used the conversion factor \(1\,\text{m}^3=1000\,\text{L}\). Hence, this is the volume in litters of the chunk of water that we needed to find.

Finally, we follow the last step, step 4. We assume that as the mass \(m\) of water is ejected from the pump of the fountain, its height is zero and it only has kinetic energy \(K\). At the maximum height \(h\) the velocity is zero, and so the mechanical energy is just the gravitational potential energy \(U\). From the principle of mechanical energy conservation, we obtain

\begin{equation}
K=U.
\end{equation}

Using the explicit expressions for the kinetic energy \(K=\frac{1}{2}mv^2\) and for the gravitational potential energy \(U=mgh\) in this equation, we obtain

\begin{equation}
\frac{1}{2}mv^2=mgh,
\end{equation}

where \(v\) is the speed of the water as it leaves the pump of the fountain. We can cancel out the mass term \(m\) in the equation and solve for \(v\) as follows

\begin{equation}
\frac{1}{2}v^2=gh,
\end{equation}

or equivalently

\begin{equation}
v^2=2gh,
\end{equation}

which after taking the square-root on both sides becomes

\begin{equation}
v=\sqrt{2gh}.
\end{equation}

Using the numerical values we obtain

\begin{equation}
v=\sqrt{2(9.8\,\text{m/s}^2)(10\,\text{m})},
\end{equation}

\begin{equation}
v=14\,\text{m/s}.
\end{equation}

You need to be registered and logged in to take this quiz. Log in or Register