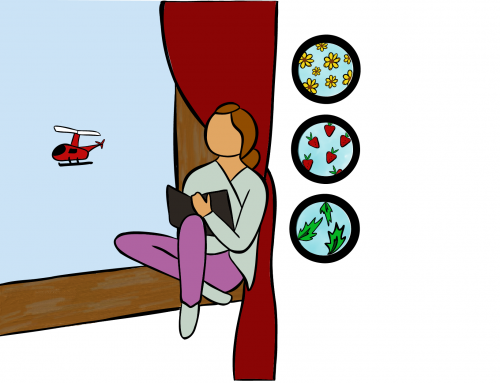
Sara is walking down the school hallway at a speed of 1 m/s when she sees her friend, Josephine, who is 10 meters ahead of Sara. Josephine misses Sara and is texting Sara to say hi. Josephine is consequently looking at her phone and doesn’t notice Sara waving hello, so she starts walking away from Josephine with a constant acceleration of \(0.2 \,\text{m}/\text{s}^2\) (see figure). Sara sees Josephine on her phone, and begins running to catch up to Josephine. Solve the physics problems below to help the two friends catch up with one another!
(a) What will Sara’s acceleration have to be if she wants to reach Josephine in 30 seconds?
(b) How many meters would Sara have to walk from the moment she sees Josephine until the moment she reaches her?
(c) Show explicitly that if Sara does not accelerate but rather keeps her constant speed, and if Josephine keeps her acceleration, Sara will never reach Josephine.
(a) Notice that when they meet, the positions of Sara and Josephine must be the same.
(b) Use the equation that gives the position of an object moving with constant acceleration.
(c) Try to find the time Sara would take to reach Josephine’s position and see if this time would make sense.
(a) Initially Sara was still, and Josephine starts moving away from her with an acceleration of magnitude \(0.2 \,\text{m}/\text{s}^2\). Hence, the equation of motion that describes the movement for both of them is that of an object with constant acceleration:
\begin{equation*}
\vec{x}_f = \vec{x}_{i} + \vec{v}_{i}t +\frac{1}{2} \vec{a} t^2.
\end{equation*}
We need to consider the time when their positions coincide using the last equation for both Sara and Josephine. Then, solving for \(a_s\) we get:
\begin{equation*}
a_s = \frac{2}{t_s^2} \left( x_{ij} + \frac{1}{2} a_j t_j^2 – v_{is} t_s \right).
\end{equation*}
And the numerical result is:
\begin{equation*}
a_s = \frac{7}{45} \; \text{m/s}^2.
\end{equation*}
(b) As we already know the acceleration, we can use the equation for an object with constant acceleration:
\begin{equation*}
\vec{x}_f = \vec{x}_{i} + \vec{v}_{i}t +\frac{1}{2} \vec{a} t^2,
\end{equation*}
where using the numerical values we get:
\begin{equation*}
x_{fs} = 100 \; \text{m}.
\end{equation*}
(c) We need to consider the time when their positions coincide using the same equation as in (a), but in contrast to (a) now Sara’s acceleration is zero. Using the numerical values we get:
\begin{equation*}
0 = {\left( 0.1\,\frac{\text{m}}{\text{s}^2} \right)} t^2 {\left( -1\,\frac{\text{m}}{\text{s}} \right)} t + {\left(10 \, \text{m} \right)},
\end{equation*}
which has no real solution. Then Sara will never reach Josephine.
For a more detailed explanation of any of these steps, click on “Detailed Solution”.
(a) First, we need to find Sara’s acceleration so that she reaches Josephine in 30 seconds. We know that initially, Sara walks with a constant speed of 1 m/s and she is 10 meters away from Josephine. We also know that Josephine starts to walk away from Sara, but Sara reaches her in 30 seconds.
Let us start by placing a coordinate system whose origin is located at Sara’s initial position, and whose X axis points in the direction of motion. According to that system, initially Josephine is \(x=10\) meters in the positive X direction, as illustrated in figure 1.
Figure 1: We place the coordinate system at Sara’s initial position with the X axis long the path that joins Sara and Josephine.
Although initially she was still, Josephine starts moving away from Sara with an acceleration of magnitude \(0.2 \,\text{m}/\text{s}^2\). Hence, the equation of motion that describes Josephine’s movement is that of an object with constant acceleration:
\begin{equation}
\label{MovimientoUniforAceleradoJosep}
\vec{x}_f = \vec{x}_{ij} + \vec{v}_{ij}t_j +\frac{1}{2} \vec{a}_j t_j^2.
\end{equation}
Here \(\vec{x}_{ij}\) is Josephine’s initial position, \(\vec{x}_{f}\) the final position, \(\vec{v}_{ij}\) the initial speed (we know it is zero), \(\vec{a}_j\) the acceleration, and \(t_j\) the time. According to our coordinate system, the acceleration, the final position, and the initial position are all positive in X, and so we can write the previous equation as
\begin{equation}
x_{fj} \, \hat{\textbf{i}} = x_{ij} \, \hat{\textbf{i}} + \frac{1}{2} a_j t_j^2 \, \hat{\textbf{i}},
\label{SaraJosefina_MovimientoJosefina}
\end{equation}
where we also used that the initial speed was zero.
Sara wants to reach Josephine in 30 seconds, and this is why she accelerates at the same time Josephine starts to walk away. So, she also has constant acceleration, and so we need to use again equation \eqref{MovimientoUniforAceleradoJosep} but adapted for Sara. According to our system, the initial position for Sara is zero, the final position is positive in X, the initial velocity is also positive in X (she moves in the direction of X), and her acceleration is also positive in X. So, her equation of motion is
\begin{equation}
x_{fs} \, \hat{\textbf{i}} = v_{is} t_s \, \hat{\textbf{i}} + \frac{1}{2} a_s t_s^2 \, \hat{\textbf{i}},
\label{SaraJosefina_MovimientoSara}
\end{equation}
where \(x_{fs}\) is the final position for Sara, \(v_{is}\) her initial speed, \(a_s\) her acceleration and \(t_s\) the time.
Since we want to find the acceleration that Sara needs to reach Josephine, we need to consider the time when their positions coincide (which is the time when they meet). That is, we want the time when
\begin{equation}
\label{SamePosition}
x_{fs} \, \hat{\textbf{i}} = x_{fj} \, \hat{\textbf{i}}.
\end{equation}
So, if we use equation \eqref{SaraJosefina_MovimientoSara} and \eqref{SaraJosefina_MovimientoJosefina} here, we get
\begin{equation}
{ v_{is} t_s \, \hat{\textbf{i}} + \frac{1}{2} a_s t_s^2 \, \hat{\textbf{i}}} = x_{ij} \, \hat{\textbf{i}} + \frac{1}{2} a_j t_j^2 \, \hat{\textbf{i}}.
\label{SaraJosefina_igualdadMovimientos}
\end{equation}
Let’s focus only on the magnitudes:
\begin{equation}
v_{is} t_s + \frac{1}{2} a_s t_s^2 = x_{ij} + \frac{1}{2} a_j t_j^2.
\label{SaraJosefina_igualdadMovimientosMagnitudes}
\end{equation}
From equation \eqref{SaraJosefina_igualdadMovimientosMagnitudes}, we want to find \(a_{s}\) (we know all the other variables). From equation \eqref{SaraJosefina_igualdadMovimientosMagnitudes}, we subtract on both sides the terms that do not have the acceleration \( a_s\). This gives us
\begin{equation}
\frac{1}{2} a_s t_s^2 = x_{ij} + \frac{1}{2} a_j t_j^2 – v_{is} t_s.
\end{equation}
Then, we multiply on both sides of the equation by \( \frac{2}{t_s^2}\), to get:
\begin{equation}
a_s = \frac{2}{t_s^2} \left( x_{ij} + \frac{1}{2} a_j t_j^2 – v_{is} t_s \right).
\end{equation}
Finally, we replace the values of the different variables, keeping in mind that the time for Josephine’s motion and Sara’s motion is the same (namely, 30 seconds):
\begin{equation}
a_s = \frac{2}{({30 \; \text{s}})^2} \bigg( {(10 \; \text{m})} + \frac{1}{2} {(0.2 \,\text{m}/\text{s}^2)} ({30 \; \text{s}})^2 – {(1 \; \text{m/s})} {(30 \; \text{s})} \bigg).
\end{equation}
The result is
\begin{equation}
a_s = \frac{7}{45} \; \text{m/s}^2. \label{SaraJosefina_AceleracionSara}
\end{equation}
This is just the magnitude of Sara’s acceleration. The direction is positive in X.
(b) We want to find the distance that Sara travels from the moment she sees Josephine to the moment she reaches her. Since we already know the acceleration, we can use equation \eqref{SaraJosefina_MovimientoSara}. We know that \(x_{is}=0\), \(v_{is}=1\) m/s (and the velocity is positive in X), \(t_s=30\) seconds, \(a_s= \frac{7}{45} \, \text{m/s}^2 \) (and positive in X) and we need to find \(x_{fs}\):
\begin{equation}
x_{fs} \hat{\textbf{i}} = + {(1 \; \text{m/s})} {(30 \; \text{s})} \,\hat{\textbf{i}} + \frac{1}{2} {\left(\frac{7}{45} \; \text{m/s}^2 \right)} ({30 \; \text{s}})^2 \,\hat{\textbf{i}}.
\end{equation}
The result is
\begin{equation}
x_{fs} \,\hat{\textbf{i}} = 100 \; \text{m} \, \hat{\textbf{i}}.
\label{SaraJosefina_PosFinalSara}
\end{equation}
That is, Sara has walked one hundred meters in the positive X direction.
(c) If Sara does not accelerate, we can set \(a_s = 0\). Equation \eqref{SaraJosefina_igualdadMovimientosMagnitudes} was obtained by assuming that Sara and Josephine’s final positions were the same. Furthermore, the time in that equation is the same for both of them (\(t_s=t_j = t\)). Let’s try to find the time in which they would meet under these new circumstances (no acceleration for Sara). If the time we obtain makes sense (if it is a real number and positive), then we can infer that Josephine can indeed reach Josephine.
If we move all the terms in equation \eqref{SaraJosefina_igualdadMovimientosMagnitudes} to the right, we get
\begin{equation}
0 = x_{ij} + \frac{1}{2} a_j t^2 – v_{is} t – \frac{1}{2} a_s t^2.
\end{equation}
Let’s use the fact that Sara has no acceleration and rearrange a bit to get
\begin{equation}
0 = \frac{1}{2} a_j t^2 – v_{is}t + x_{ij}. \label{SaraJosefina_cuadratica}
\end{equation}
This is a quadratic equation for the time (recall that a quadratic equation is of the form \(ax^2+bx+c=0\)). If we insert the known values, we get
\begin{equation}
0 = {\left( 0.1\,\frac{\text{m}}{\text{s}^2} \right)} t^2 {\left( -1\,\frac{\text{m}}{\text{s}} \right)} t + {\left(10 \, \text{m} \right)}.
\label{SaraJosefina_cuadraticaReemplazarTodo}
\end{equation}
But this equation has no real solution, and the time could not be imaginary! Hence, Sara cannot reach Josephine.




Leave A Comment