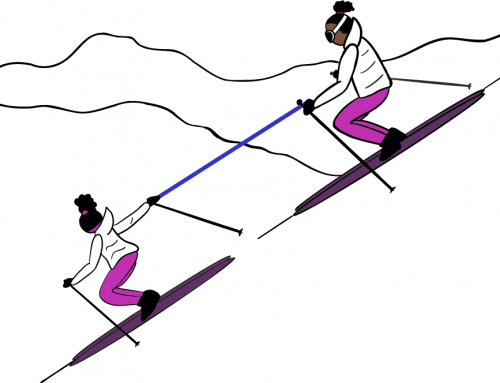
Una moto de nieve que se mueve a velocidad constante arrastra una carga, como se muestra en la imagen. El coeficiente de fricción dinámica entre la carga y el hielo es \(\mu\).
(a) Calcule la tensión en la cuerda que conecta la carga a la moto de nieve, en términos de m, g, \(\theta\) y \(\mu\).
(b) Analice lo que sucedería si \(\theta\) estuviera cerca a cero y si estuviera cerca a 90 grados.
a) La tensión es la única fuerza que tiene componentes a lo largo de los ejes \({x-} \) y \({y-} \) . Dibuje un diagrama de cuerpo libre y divida los vectores de fuerza en componentes para encontrar la fuerza de tensión.
b) Evalúe cada caso usando la ecuación obtenida para la fuerza de tensión de la parte (a).
a) La segunda ley de Newton en la dirección \({x-} \), recordando que el objeto se mueve a velocidad constante, se puede escribir como:
\begin{equation*}
-f_r+T\cos(\theta)=0,
\end{equation*}
[mepr-show rules=”4409″ unauth=”both”]
donde \(f_r = \mu N\). La segunda ley de Newton en la dirección \({y-} \) es:
\begin{equation*}
N + T \sin \theta – mg = 0.
\end{equation*}
Despejando \(N \) sustituyéndola en la primera ecuación, y luego despejando \(T \) se obtiene:
\begin{equation*}
T=\frac{\mu mg}{\sin(\theta)+\cos(\theta)}.
\end{equation*}
b) Si \(\theta \to 0 \), entonces:
\begin{equation*}
T=\mu mg,
\end{equation*}
lo que significa que \(T \) debe ser horizontal.
Si \(\theta \to 90 ^ \circ \), entonces no habrá fuerzas en la dirección \({x-} \). Por tanto, la carga no se mueve a velocidad constante. Considere que \(N> 0 \) está en contacto con el suelo, y dada la ecuación en la dirección \({y-} \), obtenemos la siguiente condición:
\begin{equation*}
mg-T\sin(\theta)>0,
\end{equation*}
Reemplazo de \(T\):
\begin{equation*}
mg-\frac{\mu mg\sin(\theta)}{\sin(\theta)+\cos(\theta)}>0.
\end{equation*}
Reordenando la ecuación con algo de álgebra, obtenemos:
\begin{equation*}
\sin(\theta)+\cos(\theta)>\mu \sin(\theta).
\end{equation*}
El caso crítico ocurre cuando \(\theta = 90 ^ {\circ} \), por lo que debemos evaluar la desigualdad en este ángulo, lo que da:
\begin{equation*}
1>\mu.
\end{equation*}
Por lo tanto, siempre que el coeficiente de fricción sea menor que 1, la carga hará contacto con el piso para todos los ángulos \(\theta \) entre \(0 ^ {\circ} \) y \(90 ^ {\circ } \).
Para obtener una explicación más detallada de cualquiera de estos pasos, haga clic en “Solución detallada”.
[/mepr-show]
1. Estrategia general para (a)
a) Nos han pedido que encontremos la tensión en la cuerda. Para resolver este problema, comenzaremos por hacer un diagrama de cuerpo libre para identificar todas las fuerzas ejercidas sobre la carga. Luego, usaremos la segunda ley de Newton en los ejes X y Y para despejar la tensión \(T\).
2. Identificar las fuerzas y realizar un diagrama de cuerpo libre
Para hacer el diagrama de cuerpo libre, primero identificamos las fuerzas (usaremos un sistema de coordenadas con Y apuntando hacia arriba y X apuntando en la dirección del movimiento). Las fuerzas son las siguientes:
- El peso \(W=mg\) dirigido al eje Y negativo. Aquí \(m\) es la masa de la carga y \(g\) la aceleración gravitacional de la Tierra.
- La fuerza de contacto con el piso \(N\), que es normal a la superficie y, por lo tanto, se dirige a lo largo del eje Y positivo.
- La fricción dinámica \(f_r\) dirigida a lo largo del eje X negativo (oponiéndose al movimiento entre las superficies). Su magnitud será el coeficiente de fricción dinámica \(\mu\) multiplicado por la fuerza de contacto \(N\), es decir \(fr=\mu N\).
- La tensión ejercida por la cuerda \(T\) en un ángulo \(\theta\) del eje X. Así, podemos descomponer la fuerza en componentes.
[mepr-show rules=”4409″ unauth=”both”]
Por tanto, el diagrama de cuerpo libre se puede mostrar en la figura 1.
Figura 1: diagrama de cuerpo libre de la carga con las siguientes fuerzas: el peso \(\vec{W}\), la fuerza de contacto con el suelo \(\vec{N}\), la tensión \(\vec{T}\) y la fricción \(\vec{f}_r\). También podemos ver el ángulo que forma la tensión con el eje horizontal y su descomposición a lo largo de los ejes X y Y. Elegimos el sistema de coordenadas de modo que X esté a lo largo de la dirección del movimiento y Y apunte hacia arriba.
3. Segunda ley de Newton en X
Podemos escribir, entonces, la segunda ley de Newton para el eje X como
\begin{equation}
\label{newtonx1}
-f_r\,\hat{\textbf{i}}+T_x\,\hat{\textbf{i}}=ma_x\,\hat{\textbf{i}},
\end{equation}
donde \(a_x\) es la aceleración a lo largo del eje X y \(T_x\) la tensión en X. En el diagrama de cuerpo libre, vemos que la componente a lo largo del eje X será \(T\cos(\theta)\).
Por lo tanto, la ecuación anterior se convierte en
\begin{equation}
\label{newtonx}
-f_r\,\hat{\textbf{i}}+T\cos(\theta)\,\hat{\textbf{i}}=ma_x\,\hat{\textbf{i}}.
\end{equation}
Debido a que la moto de nieve se mueve a velocidad constante, también lo hace la carga, lo que significa que la aceleración es cero \(a_x=0\). Por lo tanto, la ecuación \eqref{newtonx} se puede escribir como
\begin{equation}
-f_r\,\hat{\textbf{i}}+T\cos(\theta)\,\hat{\textbf{i}}=0\,\hat{\textbf{i}},
\end{equation}
o, al descartar la notación vectorial y centrándonos en la magnitud de cada vector, obtenemos
\begin{equation}
-f_r+T\cos(\theta)=0.
\end{equation}
Además, podemos usar ese \(fr=\mu N\) para escribir la ecuación anterior como
\begin{equation}
\label{newtonx2}
-(\mu N)+T\cos(\theta)=0.
\end{equation}
4. Segunda ley de Newton en Y
Ahora, escribimos la segunda ley de Newton para el eje Y:
\begin{equation}
-mg\,\hat{\textbf{j}}+N\,\hat{\textbf{j}}+T_y\,\hat{\textbf{j}}=ma_y\,\hat{\textbf{j}},
\end{equation}
donde \(a_y\) es la aceleración a lo largo del eje Y y \(T_y\) la componente Y de la tensión. En el diagrama de cuerpo libre, vemos que esta componente es igual a \(T\sin(\theta) \).
\begin{equation}
-mg\,\hat{\textbf{j}}+N\,\hat{\textbf{j}}+T\sin(\theta)\,\hat{\textbf{j}}=ma_y\,\hat{\textbf{j}}.
\end{equation}
Dado que la carga no se mueve verticalmente a lo largo del eje Y, su aceleración en esta dirección es cero \(a_y=0\). Por lo tanto, podemos escribir la segunda ley de Newton para el eje Y como
\begin{equation}
-mg\,\hat{\textbf{j}}+N\,\hat{\textbf{j}}+T\sin(\theta)\,\hat{\textbf{j}}=0\,\hat{\textbf{j}},
\end{equation}
o, al descartar la notación vectorial y enfocándonos en las magnitudes,
\begin{equation}
-mg+N+T\sin(\theta)=0.
\end{equation}
5. Manipular las ecuaciones
Podemos despejar \(N\) en la ecuación anterior. Explícitamente,
\begin{equation}
\label{normal}
N=mg-T\sin(\theta).
\end{equation}
Al usar este resultado para \(N\) en la ecuación \eqref{newtonx2}, obtenemos
\begin{equation}
-\mu(mg-T\sin(\theta))+T\cos(\theta)=0.
\end{equation}
Al expandir el término entre paréntesis en la expresión anterior, obtenemos
\begin{equation}
\label{casi}
-\mu mg+T\sin(\theta)+T\cos(\theta)=0.
\end{equation}
De la ecuación \eqref{casi} podemos despejar la tensión \(T\) en términos de las variables requeridas. Comencemos por factorizar \(T\) en los dos últimos términos de la ecuación \eqref{casi} para obtener
\begin{equation}
-\mu mg +T(\sin(\theta)+\cos(\theta))=0.
\end{equation}
Ahora, sumemos \(\mu m g\) en ambos lados de la ecuación para obtener
\begin{equation}
T(\sin(\theta)+\cos(\theta))=\mu mg.
\end{equation}
Al dividir ambos lados por el término \(\sin(\theta)+\cos(\theta)\), finalmente obtenemos
\begin{equation}
\label{result}
T=\frac{\mu mg}{\sin(\theta)+\cos(\theta)}.
\end{equation}
6. Estrategia general para (b)
b) Para la última parte del problema, necesitamos discutir qué pasaría si \(\theta\) está cerca de cero y 90 grados. Por lo tanto, necesitamos adaptar la ecuación de \(T\) para este caso.
7. Adaptar las ecuaciones anteriores a la nueva situación
A medida que el ángulo \(\theta\) se acerca a cero, la expresión para \(T\) se convierte en
\begin{equation}
T=\frac{\mu mg}{\sin(0^{\circ})+\cos(0^{\circ})},
\end{equation}
que es igual a
\begin{equation}
\label{t0}
T=\frac{\mu m g}{0+1}=\mu mg.
\end{equation}
Note que cuando \(T\) se acerca a cero, la dirección de la tensión será totalmente horizontal. Así, en el eje Y solo habrá dos fuerzas, la fuerza de contacto \(N\) y el peso \(mg\). A partir de la condición de equilibrio (el hecho de que no haya aceleración), podemos concluir que estas dos fuerzas deben ser iguales, por lo que \(N=mg\). En el eje X también habrá solo dos fuerzas: la fricción \(f_r\) y la tensión \(T\). El resultado de la ecuación \eqref{t0} evidencia este hecho porque de \(f_r=\mu N\) y los resultados para el eje Y, obtenemos \(f_r=\mu mg\).
A medida que aumenta el ángulo, el valor de \(T\) disminuye y alcanza un valor mínimo en \(\theta=45\) grados. Para un ángulo cercano a \(\theta=90\) grados, la tensión estará principalmente a lo largo del eje Y. Usando el resultado de la ecuación \eqref{result}, obtenemos
\begin{equation}
T=\frac{\mu mg}{\sin(90^{\circ})+\cos(90^{\circ})},
\end{equation}
que se simplifica a
\begin{equation}
T=\frac{\mu m g}{1+0}=\mu m g.
\end{equation}
Cuando el ángulo se acerca a los 90 grados, la tensión vuelve a ser máxima. Sin embargo, debemos tener mucho cuidado con este caso porque, a medida que la tensión se acerca a 90 grados, la fricción con el piso disminuye, volviéndose cero cuando \(\theta=90^{\circ}\), ¡lo que significa que no se ejercerán fuerzas en la carga a lo largo del eje X! Y esto contradice el hecho de que la carga se esté moviendo a velocidad constante sobre una superficie con fricción. Otro punto crucial a tener en cuenta en este análisis es que la carga debe estar en contacto con el piso en todos los ángulos, es decir \(N>0\), en todo momento. Al usar el resultado de \(N\) dado en la ecuación \eqref{normal}, obtenemos la siguiente condición:
\begin{equation}
mg-T\sin(\theta)>0,
\end{equation}
Ahora usemos nuestro resultado para \(T\) dado por la ecuación \eqref{result} para obtener
\begin{equation}
mg-\frac{\mu mg\sin(\theta)}{\sin(\theta)+\cos(\theta)}>0.
\end{equation}
Como \(m\) y \(g\) son constantes positivas, la condición se simplifica a
\begin{equation}
1-\frac{\mu \sin(\theta)}{\sin(\theta)+\cos(\theta)}>0,
\end{equation}
que es equivalente a
\begin{equation}
1>\frac{\mu \sin(\theta)}{\sin(\theta)+\cos(\theta)}.
\end{equation}
Debido a que el término en el denominador \(\sin(\theta)+\cos(\theta)\) siempre es mayor que cero, podemos multiplicar por este en ambos lados de la desigualdad para obtener
\begin{equation}
\sin(\theta)+\cos(\theta)>\mu \sin(\theta).
\end{equation}
Debido a que el caso crítico es cuando \(\theta=90^{\circ}\), evaluamos la desigualdad en este ángulo, para obtener
\begin{equation}
\sin(90^{\circ})+\cos(90^{\circ})>\mu \sin(90^{\circ}),
\end{equation}
que nos da
\begin{equation}
1>\mu.
\end{equation}
Por lo tanto, siempre que el coeficiente de fricción sea menor que 1, la carga hará contacto con el piso para todos los ángulos \(\theta\) entre \(0^{\circ}\) y \(90^{\circ}\).
[/mepr-show]





Leave A Comment